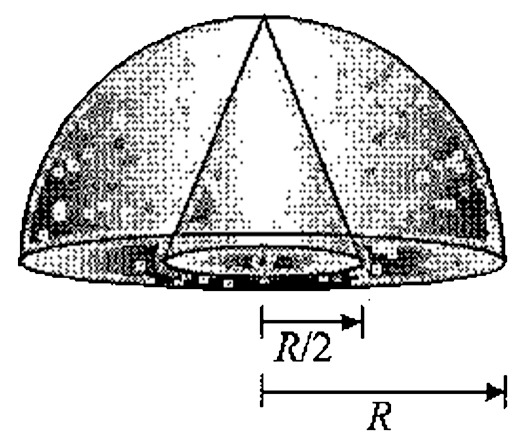
A ball of mass m and radius r rolls inside a hemispherical shell of radius R. It is released from rest from point A as shown in figure. The angular velocity of centre of the ball in position B about the centre of the shell is.
 .
.
2√g5(R−r)
2√g7(R−r)
√2g5(R−r)
√5g2(R−r)
The correct Answer is:B
KE of ball in position B=mg(R−r)
Here m=mass of ball.
Since it rolls without slipping the ratio rotational to translational kinetic energy will be 25
KRKT=25
KT=27mg(R−r),12mv2=27mg(R−r)
v=2√7√g(R−r),ω=vR−r=2√v7(R−r)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
Knowledge Check
A ball of mass m and radius r rolls inside a fixed hemispherical shell of radius R. It is released from rest from point A as shown in figure. The angular velocity of centre of the ball in position B about the centre of the shell is.
 .A2√g5(R−r)B√10g7(R−r)C√g7(R−r)D√5g2(R−r)
.A2√g5(R−r)B√10g7(R−r)C√g7(R−r)D√5g2(R−r)The distance of the centre of mass of a hemispherical shell of radius R from its centre is
AR2BR3C2R2D2R3A small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.
 AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at B
AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at B
A thin spherical shell of total mass M and radius R is held fixed. There is a small hole in the shell. A mass m is released from rest a distance R from the hole along a line that passes through the hole and also through the centre of the shell. This mass subsequently moves under the gravitational force of the shell. How long does the mass take to travel from the hole to the point diametrically opposite.
View SolutionA point charge Q is placed inside a conducting spherical shell of inner radius 3R and outer radius 5R at a distance R from the centre of the shell. The electric potential at the centre of the shell will be
View Solutiona solid sphere of mass m and radius r is plced nside as hollow thin spherical shell of mass and M and radius R as shown in figure. A particle of mas m is placed on tehline joining the tow centres ast a distance x from the point of contct of th sphere and teh shell. Findn teh mgnitude fo the resultant gravitational force on this particle due to the sphere and the shell if a. r<x<2r,b.2r<x<2Randc.x>2R.

View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure. Choose the wrong option (s)
View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

r<x<2r
View Solution