Consider three uniform solid spheres. sphere (i ) has radius and mass sphere (ii) has radius and mass , sphere (iii) has radius and mass . All the spheres can be placed at the same point on the same inclined plane where they will roll without slipping to the bottom. If allowed to roll down the incline, then at the 'bottom of the incline
sphere (i) will have the largest speed
sphere (ii) will have the largest speed
sphere (ii) will have the largest kinetic energy
all the spheres will have equal speed
The correct Answer is:C, D
radius of gyration.For all solid spheres, independent of and .
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.


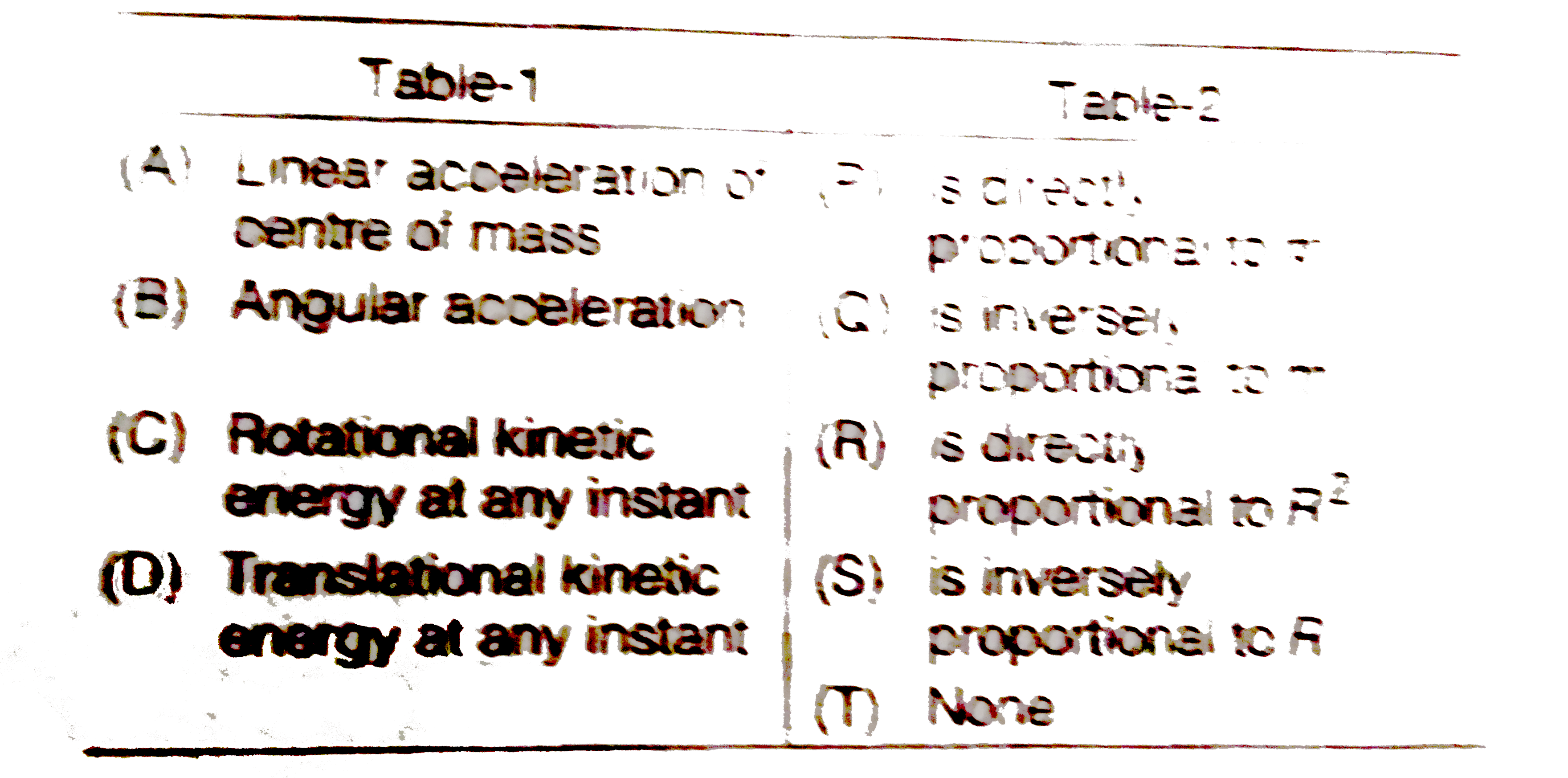
View SolutionA solid sphere of mass M and radius R, rolling down a smooth inclined plane, without slipping, reaches the bottom with a velocity v. What is the height of the inclined plane in terms of the velocity v ?
View Solution
Knowledge Check
Consider three solid spheres, sphere (i) has radius r and mass m, sphere (ii) has radius r and mass 3 m, sphere (iii) has radius 3r and mass m, All can be placed at the same point on the same inclined plane, where they will roll without slipping to the bottom, If allowed to roll down the incline, then at the bottom of the incline
Asphere (i) will have the largest speedBsphere (ii) will havethe largest speedCsphere (iii) will have the largest kinetic energyDall the sphere will have equal speeds.A sphere and circular disc of same mass and radius are allowed to roll down an inclined plane from the same height without slipping. Find the ratio of times taken by these two to come to the bottom of incline :
A√14:√15B15:14C√2:1D7:9A metal disc of radius R and mass M freely rolls down from the top of an inclined plane of height h without slipping. The speed of its centre of mass on reaching the bottom of the inclined plane is
A√4gh3B√3gh4C√ghD√gh2
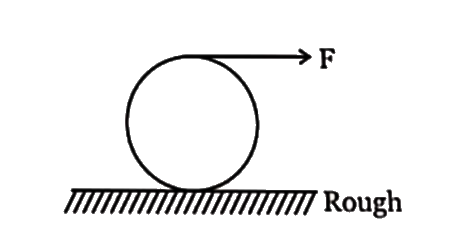
A solid sphere of radius R and mass M is rolled by a force F acting at the top of the sphere as shown in the figure. The sphere starts from rest and rolls without slipping, then
View SolutionA hollow sphere is released from top of an inclined plane of inclination 30° and length of inclined plane is I. If sphere rolls without slipping then its speed at bottom is
View SolutionA solid sphere a hollow sphere and a disc all having same mass and radius, are placed at the top of a moth incline and released. Least time will be taken in reaching the bottom by
View SolutionA solid sphere (mass 2M) and a thin spherical shell (mass M) both of the same size roll down an inclined plane, then:
View SolutionA solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View Solution
