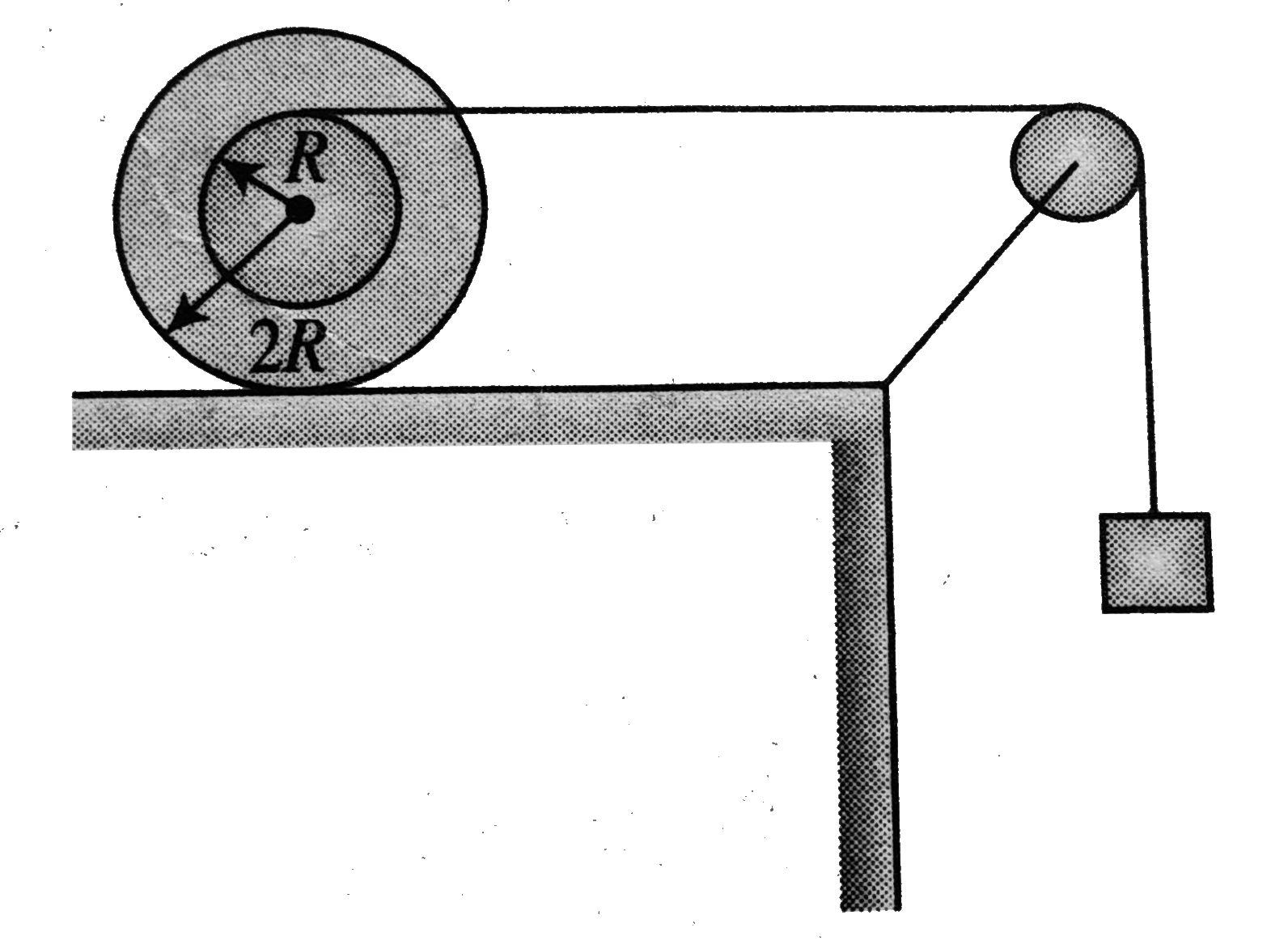
In the figure shown mass of both, the spherical body and block is m. Moment of inertia of the spherical body about centre of mass is 2mR2. The spherical body rolls on the horizontal surface. There is no slipping at any surfaces in contact. The ratio of kinetic energy of the spherical body to that of block is
3/4
1/3
2/3
1/2
The correct Answer is:C
Let v be the linear velocity of centre of mass of the sphereical body and ω its angular velocity about centre of mass. Then ω=v2R
KE of spherical body
K1=12mv2+12Iω2
K1=12mv2+12(2mR)2(v24R2)
=34mv2.....i
Speed of the block will be
v'=(ω)(3R)=3Rω=(3R)(v2R)=32v
∴KE of block K2=12mv2=12m(32v)2=98mv2 ......ii
From eqn i and ii K1K2=23
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A solid sphere rolls on horizontal surface without slipping. What is the ratio of its rotational to translation kinetic energy.
View SolutionA body is in pure rolling over a horizontal surface. If the rotational kinetic energy of that body is 40% of its total kinetic energy, then the body is
View Solution
Knowledge Check
In the figure shon mass of both, the spherical body and blocks is m. Moment of inertia of the spherical body about centre of mass is 2mR2. The spherical body rolls on the horizontal surface. There is no sliiping between any two surfaces in contact. The ratio of kinetic energy of the spherical body to that of block is
 A34B13C23D12
A34B13C23D12A plank P is placed on a solid cylinder S, which rolls on a horizontal surface. The two are of equal mass. There is no slipping at any of the surfaces in contact. The ratio of kinetic energy of P to the kinetic energy of S is:
 A1:1B2:1C8:3D11:8
A1:1B2:1C8:3D11:8For a body rolling along a level surface, without slipping the translational and rotational kinetic energies are in the ratio 2:1. The body is
AHollow sphereBsolid cylinderCringDsolid sphere
A body is rolling without slipping on a horizontal plane. The rotational energy of the body is 40% of the total kinetic energy. Identify the body
View SolutionName the dense spherical body located at the centre of the cell.
View SolutionIf a body is rolling on a surface without slipping such that its kinetic energy of translation is equal to kinetic energy of rotation then it is a
View SolutionA body si rolling without slipping on a horizontal plane. If the rotational energy of the body is 40% of the total kinetic energy then the body might be:
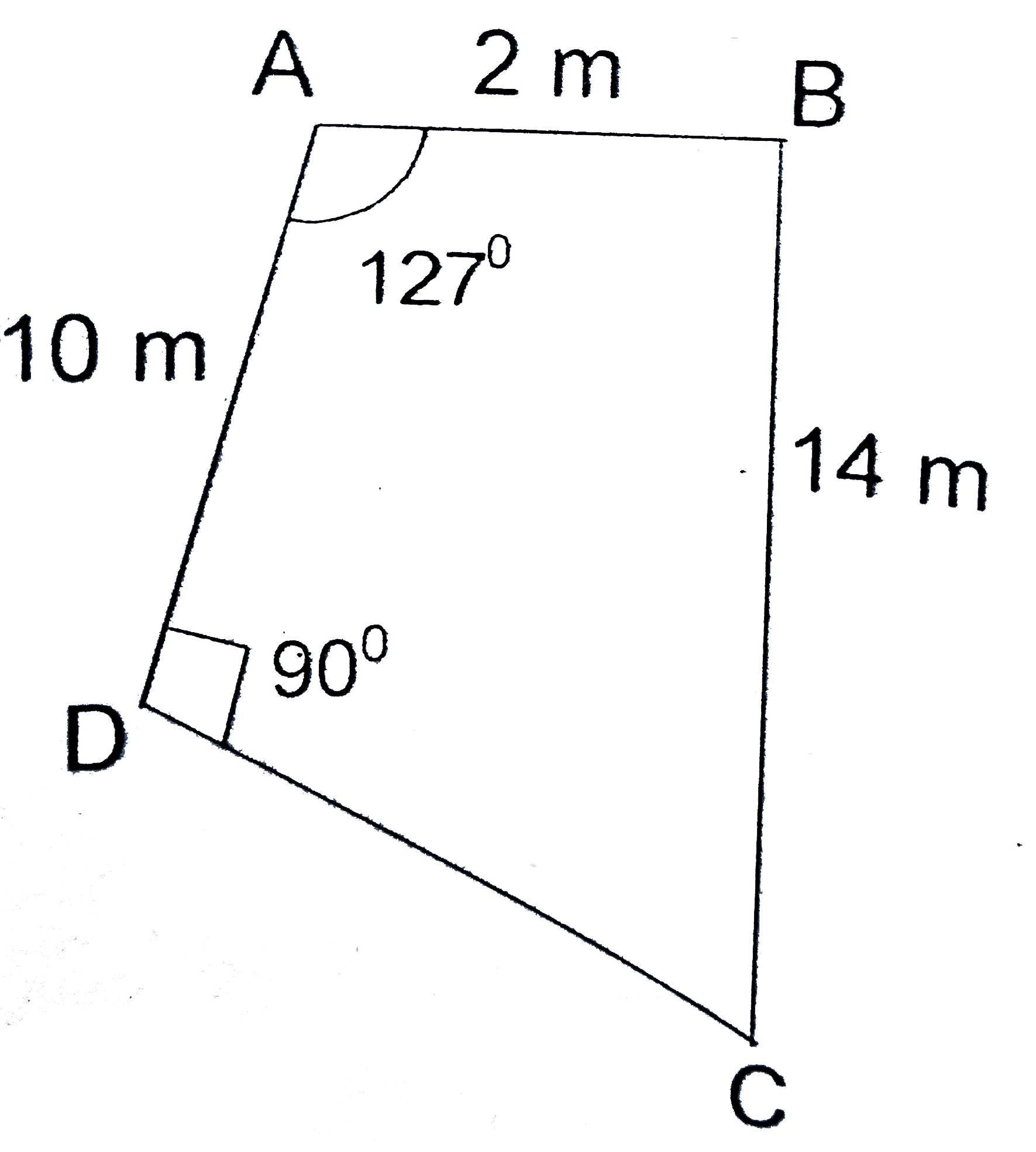
View SolutionIn the figure shown ABCD is a lamina of mass 12kg. The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is
View Solution
