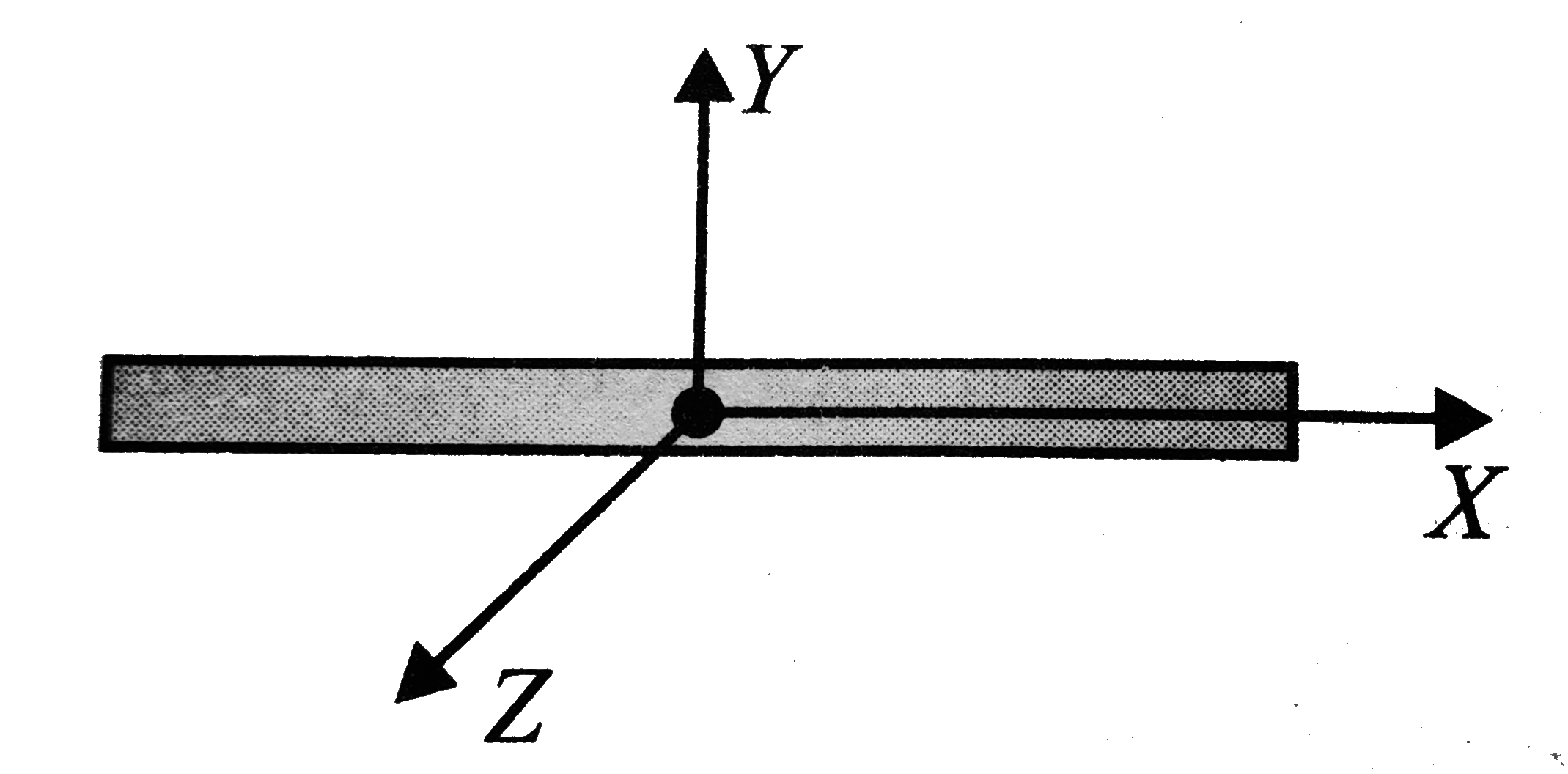
A uniform rod of mass M and length L is free to rotate in X−Z plane i.e. →F=(3ˆi+2ˆj+6ˆk)N is acting on the rod at (L/2,0,0) in the situtation shown in figure. The angular acceleration of the rod is (Take M=6kg and L=4m)
−32ˆj+12ˆk
−32ˆj
12k
4j
The correct Answer is:B
I=ML212=6×4×412=8kgm2
From →τ=→r×→LF=[2ˆi×(3ˆi+2ˆj+6ˆk)]=4ˆk−12ˆj
τ=Iα⇒−12j=8α⇒α=−32jrad/s2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A uniform rod of length L and mass M is free to rotate about a frictionless pivot at one end. The rod is released from rest in the horizontal position. What are the initial angular acceleration of the rod and the initial linear acceleration of the right end of the Rod ?
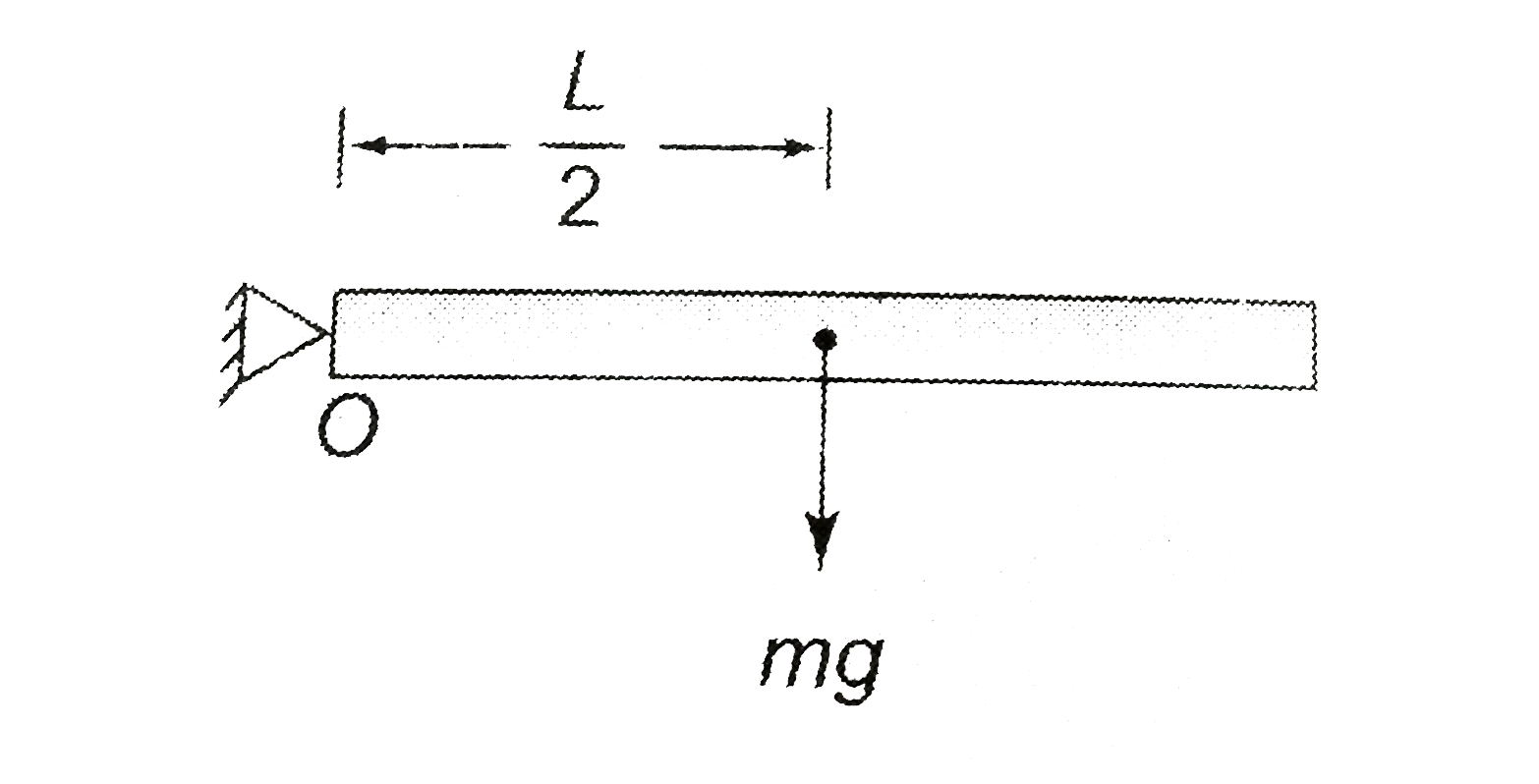
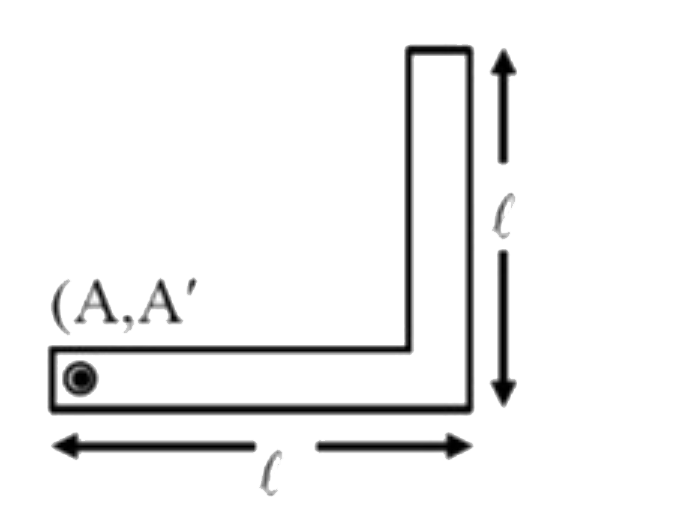
View SolutionA L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is
View Solution
Knowledge Check
A L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is
 A3g√10IB9g10lC9g5lD6g5√2I
A3g√10IB9g10lC9g5lD6g5√2IA unifrom rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is
 A3g2lB3glCg2lD2gl
A3g2lB3glCg2lD2glA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is
 A3g2LBgLC2gLD2g3L
A3g2LBgLC2gLD2g3L
Find the M.I. of thin uniform rod of mass M and length L about the axis as shown.
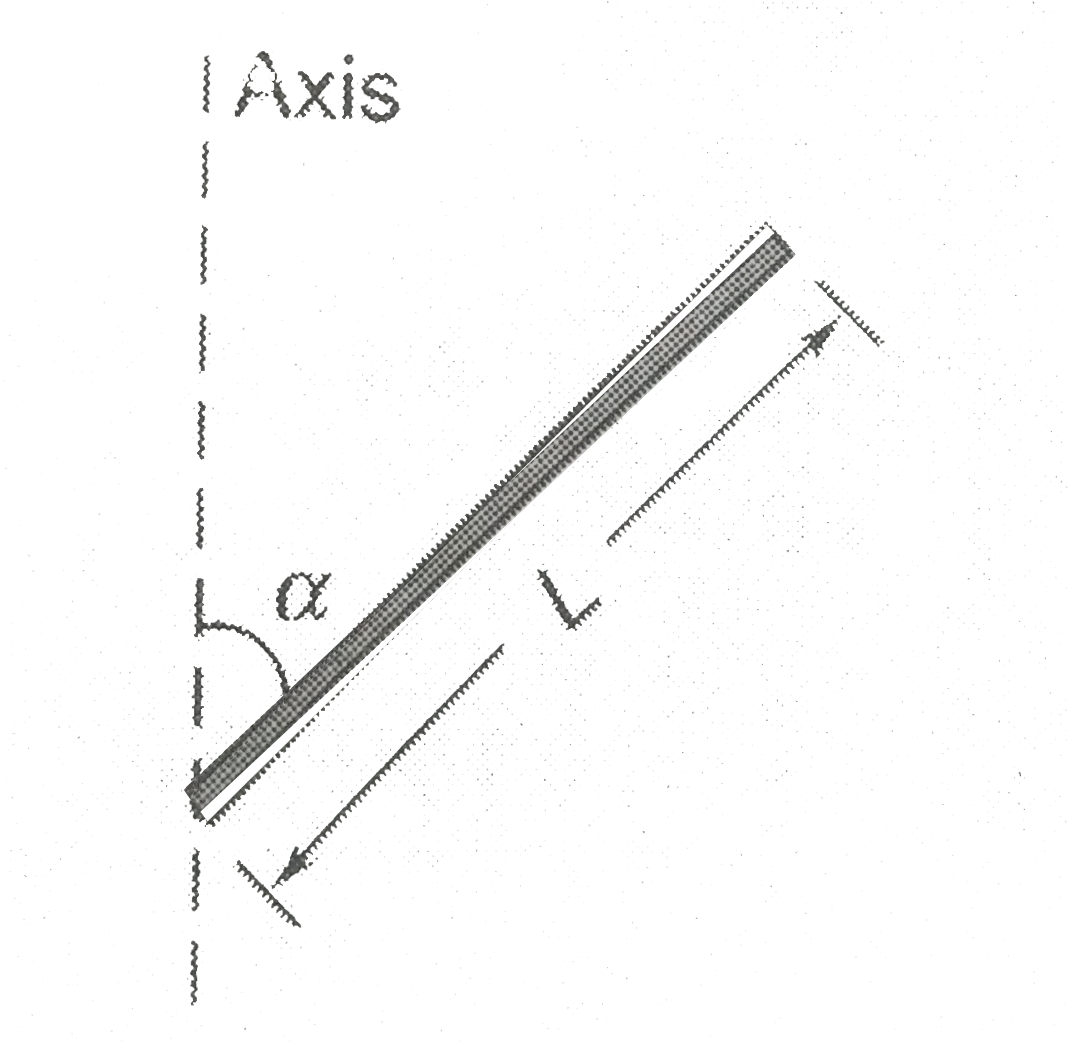
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is
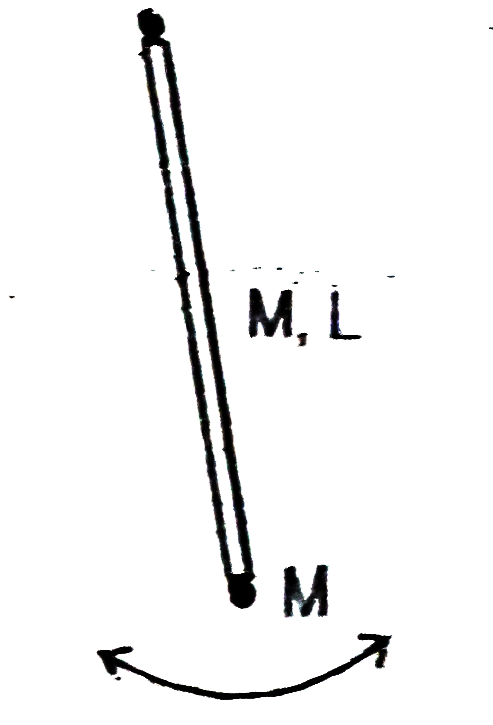
View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Ratio of elongation in section PQ of rod and section QR of rod is
View SolutionA unifrom rod of length l and mass m is free to rotate in a vertical plane about A, Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is (MIof rod aboutAisml23)
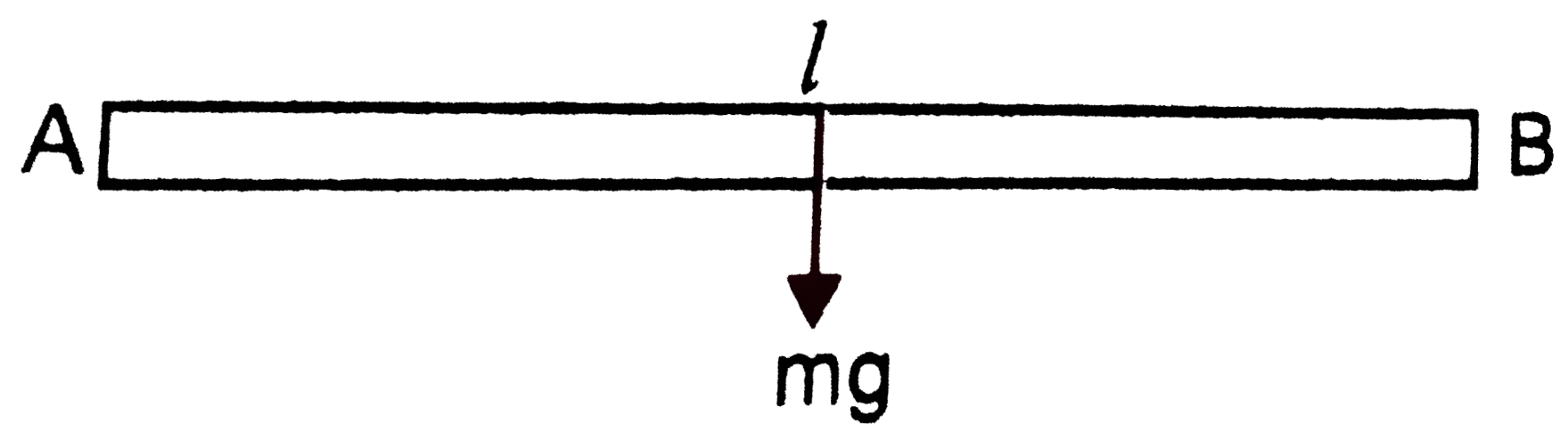
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View Solution
