A cylinder of mass M and radius R is resting on a horizontal platform (which is parallel to the x-y plane) with its axis fixed along the y-axis and free to rotate about its axis. The platform is given a motion in the x-direction given by x=Acos(ωt). There is no slipping between the cylinder and platform. The maximum torque acting on the cylinder during its motion is ..................
Mω2AR3
Mω2AR2
23×Mω2AR
The situation is not possible
The correct Answer is:B
The cylinder is having a fixed axis, so it can perform rotational motion only.
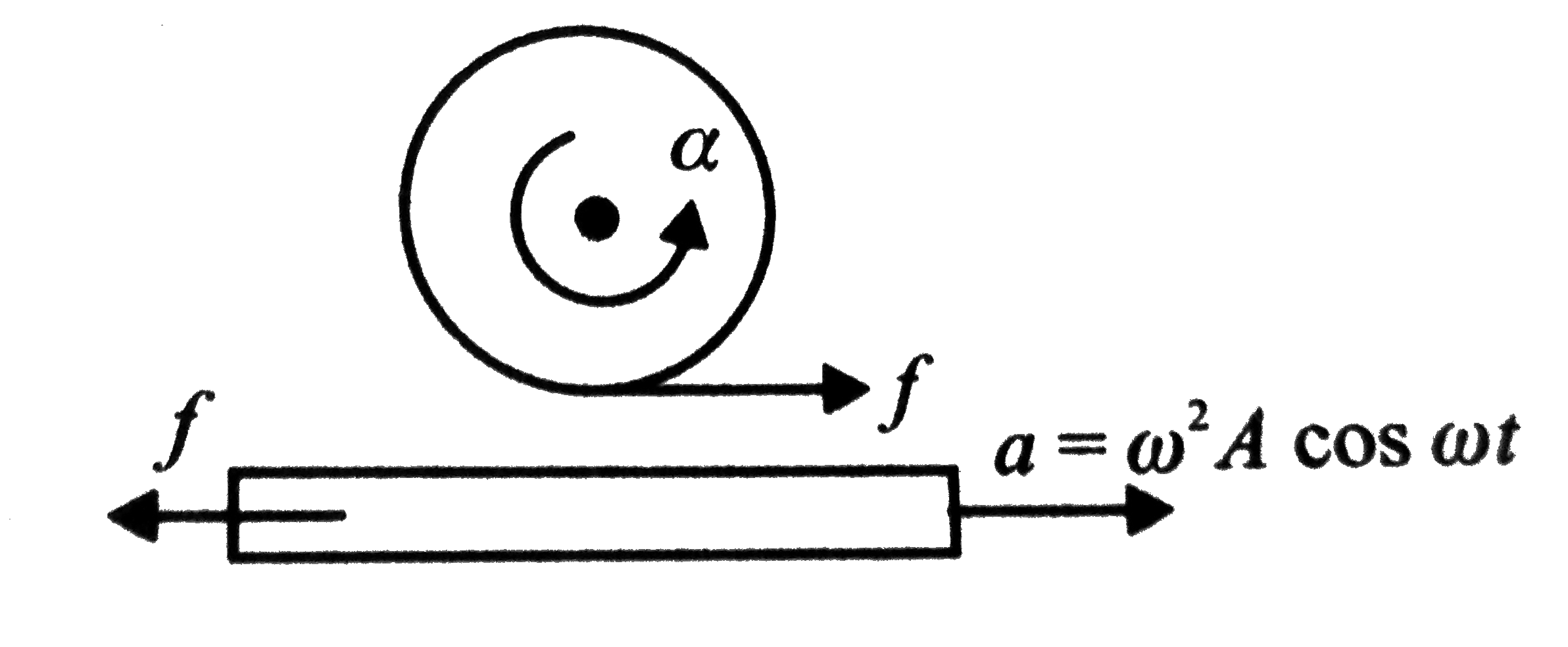
fR=MR22α⇒f=MR2α
For no slipping,
Rα= acceleration of the platform
2fM=ω2Acosωt
For the maximum torque f would maximum and fmax=Mω2A2
So the maximum torque,
τmax=fmax×R≡M2ω2AR2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A cylinder of mass M and radius R is resting on a horizontal paltform (which is parallel to the x-y plane) with its exis fixed along the y-axis and free to rotate about its axis. The platform is given a motion in the x-direction given by x=Acos(ωt). There is no slipping between the cylinder and platform. The maximum torque acitng on the cylinder during its motion is ..................
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View Solution
Knowledge Check
A uniform solid cylinder of mass 5kg and radius 0.1m is resting on a horizontal platform (parallel to the x-y plane) and is free to rotate about its axis along the y-axis the platform is given a motion in the x direction given by x=0.2 cos (10t) m if there is no slipping then maximum torque acting on the cylinder during its motion is
A0.2N−mB2.0N−mC5.0N−mD10.0N−mA cylinder of mass M, radius R is kept on a rough horizontal plane at one extreme end of the platfonn at t = 0. Axis of the cylinder is parallel to z-axis. The platform is oscillating in the xy-plane and its displacement from origin is represented by x = 4 cos(2πt) metres. There is no slipping between the cylinder and the platfonn. Find the acceleration of the centre of mass of cylinder at t =16s
(##TRG_PHY_MCQ_XII_C04_E04_001_Q01.png" width="80%">A−53π2B−23π2C−83π2D−43π2A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2
A cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA solid cylinder of mass 20kg rotates about its axis with angular velocity of 100 radian s−1. The radius of the cylinder is 0.25m. The magnitude of the angular momentum of the cylinder about its axis of rotation is
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionThe M.I. of a hollow cylinder of mass M, radius R and length L about a tangential axis parallel to the length will be:
View SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
View Solution
