
A child with mass m is standing at the edge of a merry go round having moment of inertia I, radius R and initial angular velocity ω as shown in the figure. The child jumps off the edge of the merry go round with tangential velocity v with respect to the ground. The new angular velocity of the merry go round is
√Iω2−mv2I
√(I+mR2)ω2−mv2I
Iω−mvRI
(I+mR2)ω−mvRI
The correct Answer is:D
Let the angular velocity of disc after child jumps off be ω
∴ From conservation of angular mometum
(I=mR2)ω=mvR=Iω'
∴ω'=(I+mR)−ω−mvRI
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Multiple Correct
Explore 26 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Linked Comprehension
Explore 71 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Subjective
Explore 19 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A person of mass m stands at the edge of a circular platform of radius R and moment of inertia. A platform is at rest initially. But the platform rotate when the person jumps off from the platform tangentially with velocity u with respect to platfrom. Determine the angular velocity of the platform.
View SolutionA flat car of mass m is at rest on a frictionless floor with a child of mass m standing at its edge. If the child jumps off from the car towards right with an initial velocity u, with respect to the car, find the velocity of the car after its jump.
View Solution
Knowledge Check
A child with mass m is standing at the edge of a disc with moment of inertia I, radius Rm and initial angular velocity ω. See figure given below. The chlid jumps off the edge of the disc with tangential velocity v with respect to the ground. The new angular velocity of the disc is.
 .A√Iω2−mv2IB√(I+mR2)ω2−mv2ICIω−mvRID(I+mR2)ω−mvRI
.A√Iω2−mv2IB√(I+mR2)ω2−mv2ICIω−mvRID(I+mR2)ω−mvRIThe angular momentum of a body with mass (m) moment of inertia (I) and angular velocity (ω) rad/s is equal to
AIωBIω2CIωD1ω2A body of mass m and radius r is rotated with angular velocity ω as shown in the figure & kept on a surface that has sufficient friction then the body will move
 Abackwards first and then move forwardBforward first and then move backwardCwill always move forwardDnone of these
Abackwards first and then move forwardBforward first and then move backwardCwill always move forwardDnone of these
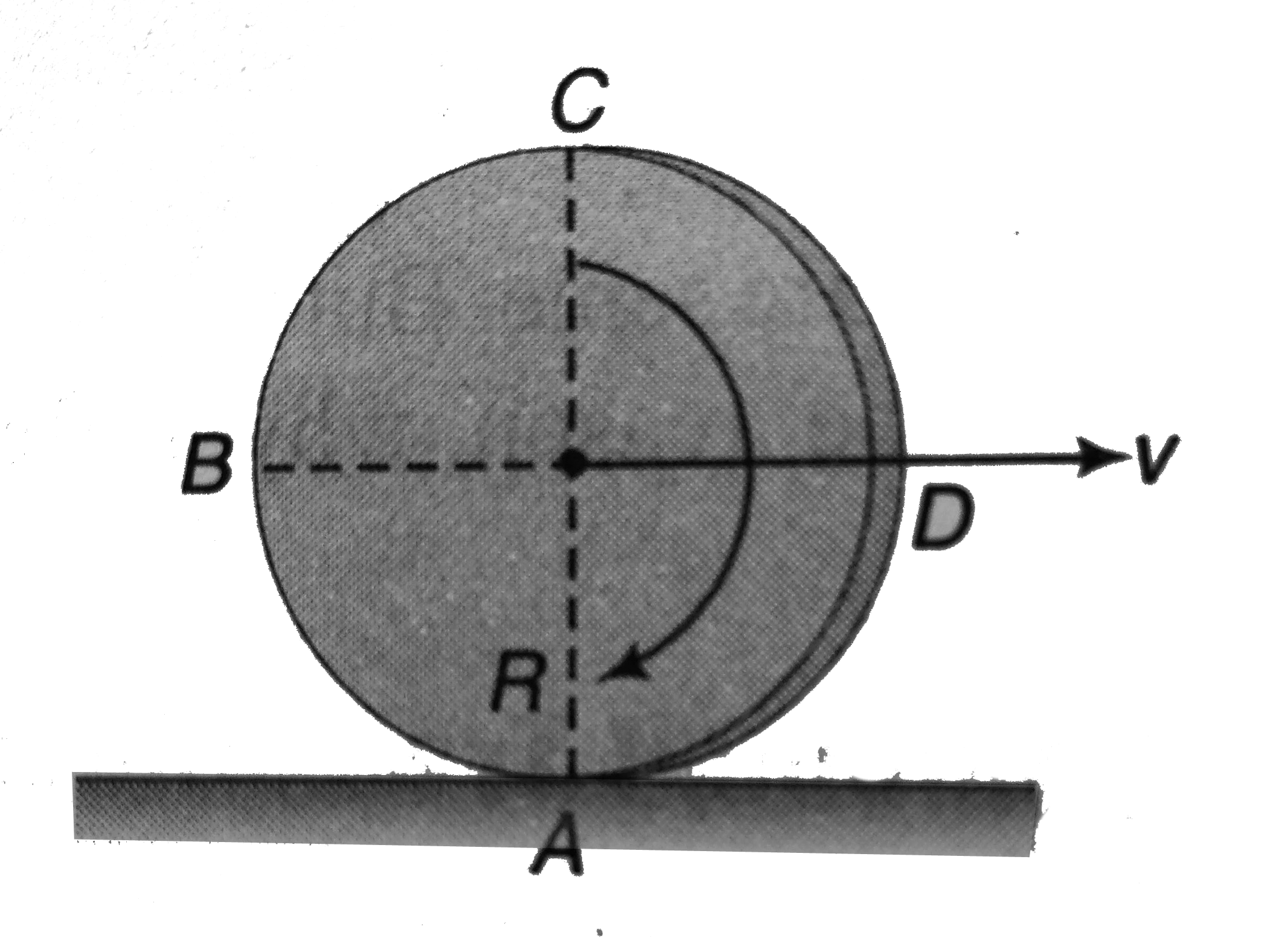
A disc of radius R has linear velocity v and angular velocity ω as shown in the figure. Given υ=rω find velocity of point A, B, C and D on the disc.
View SolutionA disc of mass M and radius R is rotating about its axis with initial angular velocity of ω0 as shown. Now two small masses of m each one kept on the circumference diametrically opposite to eachother. Find new angular velocity
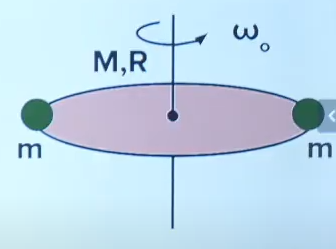
View SolutionA child is standing on the edge of a merry-go-round that has the shape of a disk, as shown in the figure. The mass of the child is 40 kg. The merry-go-round has a mass of 200kg and a radius of 2.5 m, and it is rotating with an angular velocity of ω=2.0 radians per second. The child then walks slowly towards the centre of the merry-go-round. What will be the final angular velocity of the merry-go-round when the child reaches the centre? (The size of the child can be neglected)

View SolutionA circular disc of mass M and radius R is rotating with angular velocity ω . If two small spheres each of mass m are gently attached to two diametrically opposite points on the edge of the disc, then the new angular velocity of the disc will be
View SolutionAn electron of chargee, revolves round in an orbit of radius r with a uniform angular velocity ω. The magnetic dipole moment of the electron in the orbit is
View Solution

