Discs A and B are mounted on a shaft SS and may be connected or disconnected by a clutch C. The moment of inertia of disc A is one half that of disc B. With the clutch disconnected, A is brought up to an angular velocity ω0 .The accelerating torque is then removed from A and it is coupled to disc B by the clutch (Bearing friction may be neglected). It is found that 2000J of heat is developed in the clutch when the connection is made. What is the original kinetic energy of disc A?
Let IA and IB=2I
In the connection of disk A with disk B, the agular momentum remains constant
or Iω0+0=(I+2I)ω
which gives ω=ω0/3
The change in KE eveloved as eat, i.e.,
12Iω20−12(3I)ω2=2000
Substituting the value of ω in the above equation, we get
12Iω20−12(3I)(ω03)2=2000
or 12Iω20=−12Iω2032000
∴12Iω2=3000J
Where Iω2/2 is the initial energy of the disk A.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.3
21 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.4
13 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
Discs A and B are mounted on a shaft XY and may be connected or disconnected by a coupling Z as shown in figure-5.147. The moment of inertia of disc A about the shaft is half that of disc B. The moments of inertia of the shaft and the coupling are negligible. Initially A is disconnected and rotated at an angular velocity ω. It is now coupled to disc B using couplings.It is found that 5000 J of thermal energy is developed in the coupling when the connection is made. What was the original kinetic energy of the disc A.
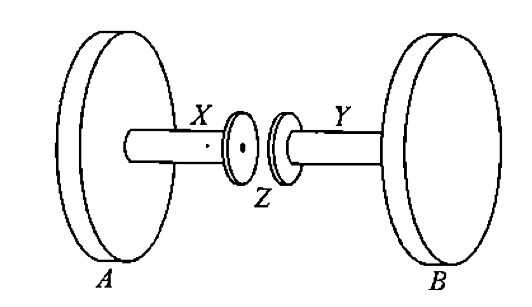
View SolutionIn the above question disc B is brought in contact with disc A, they acquire a common angular velocity in time t. The average frictional torque on one disc by the other during this periodis:
View Solution
Knowledge Check
The moment of inertia of a uniform semicircular disc of mass disc through the centre is
A25Mr2B14Mr2C12Mr2DMr2For a disc of given density and thickness, its moment of inertia varies with radius of the disc as :
A1∝R2B1∝R4C1∝R3D1∝RA ring and a disc have same mass and same radius. Then ratio of moment of inertia of ring to the moment of inertia of disc is
A4B2C0.5D1
One quarter of the disc of mass m is removed. If r be the radius of the disc, the new moment of inertia is
View SolutionAbout which of the following axes moment of inertia of a disc circular disc is minimum ?
View SolutionMoment of inertia of disc about the tangent parallel to plane is I. The moment of inertia of disc about tangent and perpendicular to its plane is
View SolutionAs shown in the figure, a disc of mass m is rolling without slipping with angular velocity ω. When it crosses point B disc will be in

View SolutionA cockroach is moving with velocity v in anticlockwise direction on the rim of a disc of radius R of mass m. The moment of inertia of the disc about the axis is I and it is rotating in clockwise direction with an angular velocity ω. If the cockroach stops, the angular velocity of the disc will be
View Solution
