The device shown in Fig. rotates on the vertical axle as shown. The frame has negligible mass as compared to the four masses each of mass m. Initial angular velocity of the system is ω0. Due to an internal mechanism the spokes in the frame lengthen so that the radii of the masses become 2a. Initially, it was a. What will be the new angular velocity of the system?
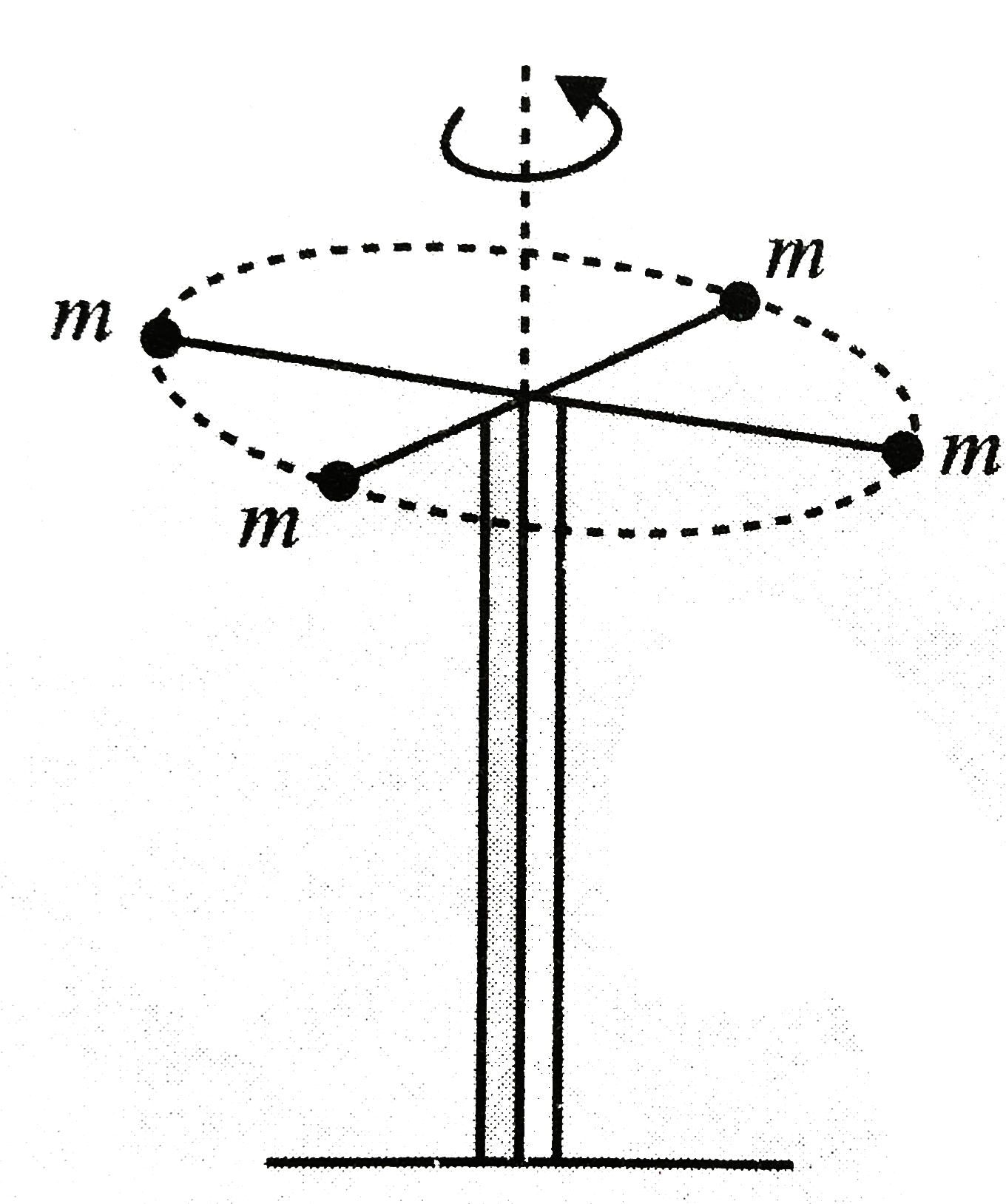
The will be no torque on the system if we ignore frictional torque at the axle. Therefore, the angular momentum of the system is conserved.
→Linitial=→Lfinal
Iinitialω0=Ifinalω
4ma2ω0=4m(2a)2ω
from which we have ω=ω04
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.3
21 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.4
13 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
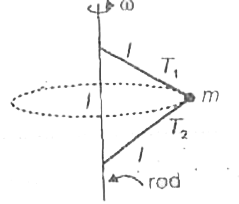
In the figure, a ball of mass m is tied with two strings of equal as shown. If the rod is rotated with angular velocity ω1 when
View SolutionIf 2 kg mass is rotating on a circular path of radius 0.8 m with angular velocity of 44 rad/sec. If radius of the parth becomes 1 m, then what will be the value of angular velocity?
View Solution
Knowledge Check
Initial angular velocity of a circular disc of mass M is ω1. Then two small spheres of mass m are attached gently to two diametrically opposite points on the edge of the disc. What is the final angular velocity of the disc -
A(M+mM)ω1B(M+mm)ω1C(MM+4m)ω1D(MM+2m)ω1Initial angular velocity of a circualr disc of mass M is ω1. The tow sphere of mass ma re attached gently to diametrically opposite points ont eh edge of the disc. What is the final angular velocity on the disc?
A(M+mM)ω1B(M+mM)ω1C(MM+4m)ω1D(MM+2m)ω1A circular disc of mass M and radius R is rotating with angular velocity ω . If two small spheres each of mass m are gently attached to two diametrically opposite points on the edge of the disc, then the new angular velocity of the disc will be
A(M+4mM)ωB(MM+4m)ωC(M+mM)ωD(MM+2m)ω
A disc of mass M and radius r is rotating with an angular velocity ω. If gently, two masses m each are placed at a distance r/2 on either side of the axis of rotation, what will be the new angular velocity ?
View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beada are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpenducular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......

View SolutionA 2 kg mass is rotating on a circular path of radius 0.8 m with angular velocity of 44 rad/sec. If radius of the path becomes 1 m, then what will be the value of angular velocity?
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?

View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......

View Solution
