One quarter of the disc of mass m is removed. If r be the radius of the disc, the new moment of inertia is
32mr2
mr22
38mr2
None of these
The correct Answer is:C
To find the new moment of inertia after removing one quarter of a disc of mass m and radius r, we can follow these steps:
Step 1: Understand the Moment of Inertia of the Whole Disc
The moment of inertia I of a full disc about an axis perpendicular to its plane and passing through its center is given by the formula:
I=12mr2
Step 2: Determine the Mass of the Removed Quarter
Since one quarter of the disc is removed, we need to calculate the mass of the removed section. The mass of the removed quarter is:
Mass of removed quarter=m4
Step 3: Calculate the Mass of the Remaining Part
After removing one quarter of the disc, the mass of the remaining part is:
Remaining mass=m−m4=3m4
Step 4: Calculate the Moment of Inertia of the Remaining Part
The moment of inertia of the remaining part (which is now a three-quarters disc) about the same axis can be calculated. Since the radius remains the same, the moment of inertia I′ of the remaining part is:
I′=12(3m4)r2
Step 5: Simplify the Expression
Now, we simplify the expression for the new moment of inertia:
I′=3m8r2
Final Answer
Thus, the new moment of inertia after removing one quarter of the disc is:
I′=3mr28
---
The moment of inertia I of a full disc about an axis perpendicular to its plane and passing through its center is given by the formula:
I=12mr2
Since one quarter of the disc is removed, we need to calculate the mass of the removed section. The mass of the removed quarter is:
Mass of removed quarter=m4
After removing one quarter of the disc, the mass of the remaining part is:
Remaining mass=m−m4=3m4
The moment of inertia of the remaining part (which is now a three-quarters disc) about the same axis can be calculated. Since the radius remains the same, the moment of inertia I′ of the remaining part is:
I′=12(3m4)r2
Now, we simplify the expression for the new moment of inertia:
I′=3m8r2
Thus, the new moment of inertia after removing one quarter of the disc is:
I′=3mr28
Topper's Solved these Questions
- ROTATIONAL MOTION'BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ROTATIONAL MOTION'EXERCISE - PRACTICE EXERCISE (Exercise 2 (MISCELLANEOUS PROBLEMS))
47 Videos
- ROTATIONAL MOTION'BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ROTATIONAL MOTION'EXERCISE - MHT CET Corner
35 Videos
- ROTATIONAL MOTION'BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ROTATIONAL MOTION'EXERCISE - MHT CET Corner
35 Videos
- REFRACTION OF LIGHTBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 2
25 Videos
- SCALARS AND VECTORS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SCALARS AND VECTORS EXERCISE - Exercise 2 (Miscellaneous Problems)
20 Videos
Similar Questions
The M.I. of a disc of mass M and radius R, about an axis passing through the centre O and perpendicular to the plane of the disc is MR22 . If one quarter of the disc is removed, the new moment of inertia of the disc will be
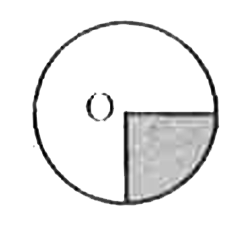
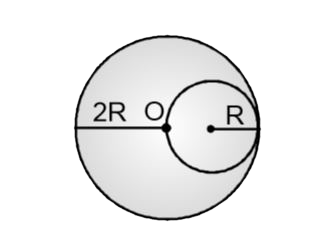
View SolutionA uniform disc having radius 2R and mass density σ as shown in figure. If a small disc of radius R is cut from the disc as shown. Then find out the moment of inertia of remaining disc around the axis that passes through O and is perpendicular to the plane of the page.
View Solution
Knowledge Check
From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
 A4M2B409MR2C10MR2D379MR2
A4M2B409MR2C10MR2D379MR2A circular disc of mass M and radius R is suspended from a nail in the wall. The nail is fixed very near to the rim of the disc. The moment of inertia of the disc about an axis along the nail is
AMR2BMR22C32MR2DMR24A solid sphere of mass M, radius R and having moment of inertia about an axis passing through the centre of mass as J, is recast into a disc of thickness t, whose moment of inertia about an axis passing through its edge and perpendicular to its plane remains J. Then, radius of the disc will be
A2R√15BR√215C4R√15DR4
A uniform circular disc has a sector of angle 90∘ removed from it. Mass of the remaining disc is M. Write the moment of inertia of the remaining disc about the axis xx shown in figure (Radius is R)

View SolutionA solid sphere of mass M, radius R and having moment of inertia about as axis passing through the centre of mass as I, is recast into a disc of thickness t, whose moment of inertia about an axis passing through its edge and perpendicular to its plance remains I. Then, radius of the disc will be.
View SolutionA solid sphere of mass M and radius R having moment of inertia about an axis passing through the centre of mass as I, is recast into a disc of thickness I, whose moment of inertia about an axis passing through its edge and perpendicular to its plane remains I. Then, radius of the disc will be
View SolutionA circular disc of radius R is removed from a bigger of the discs coincide. The centre of mass of the new disc is ar from the centre of the bigger disc. The value of α is
View SolutionA solid toy is in the form of a hemisphere surmounted by a right circular cone of same radius. The height of the cone is 10 Cm and the radius of the base is 7 cm. Determine the volume of the toy. Also find the area of the coloured sheet required to cover the toy. (Use π=22/7 and √149=12.2)
View Solution
