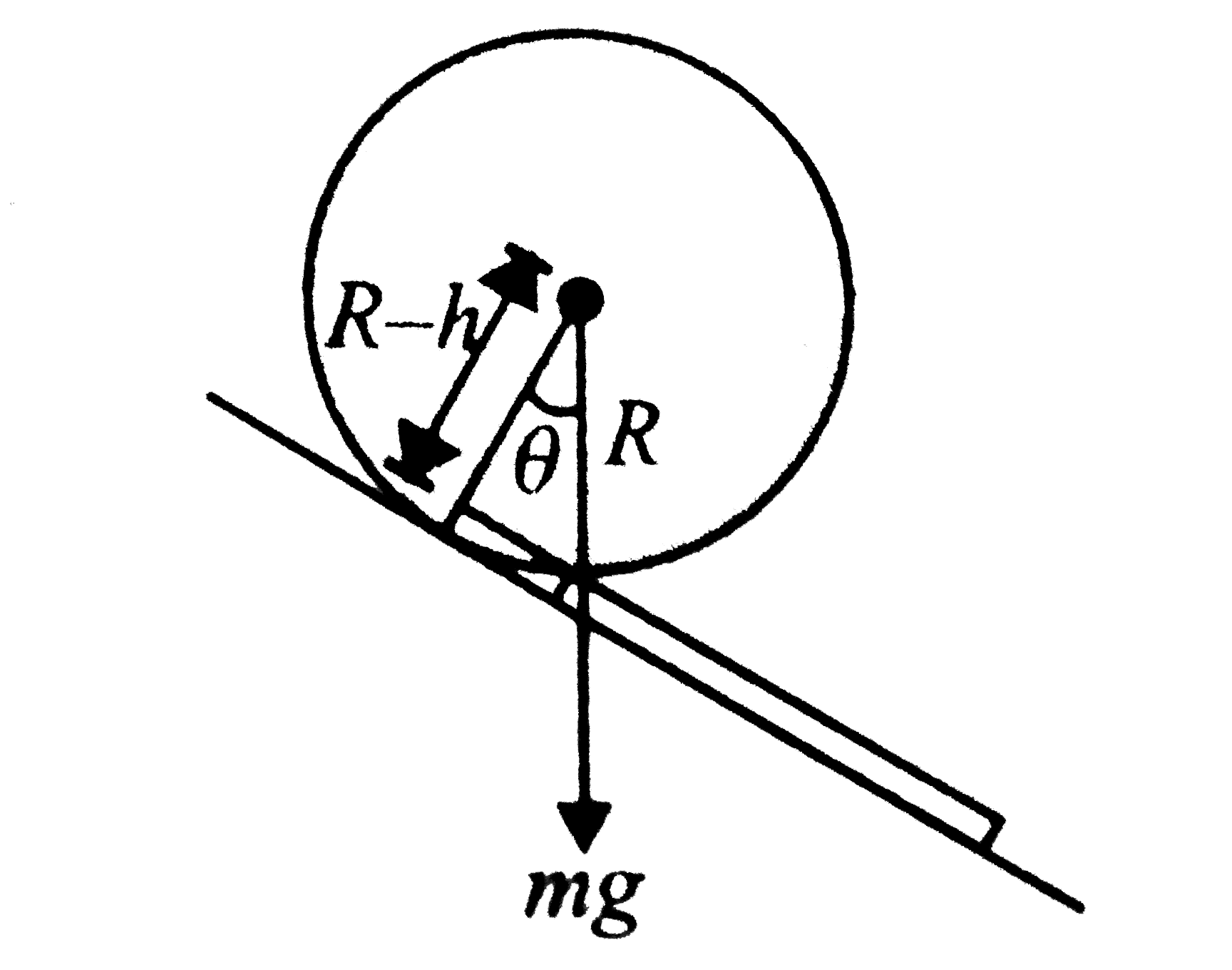
Find minimum height of the obstacle so that the sphere can stay in equilibrium

R1+cosθ
R1+sinθ
R(1−sinθ)
R(1−cosθ)
The correct Answer is:D
The sphere is on the verge of toppling when a line a action of weight passes through the edge.
cosθ=R−hR⇒h=R−Rcosθ
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Multiple Correct
Explore 9 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Linked Comprehension
Explore 28 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Subjective
Explore 13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
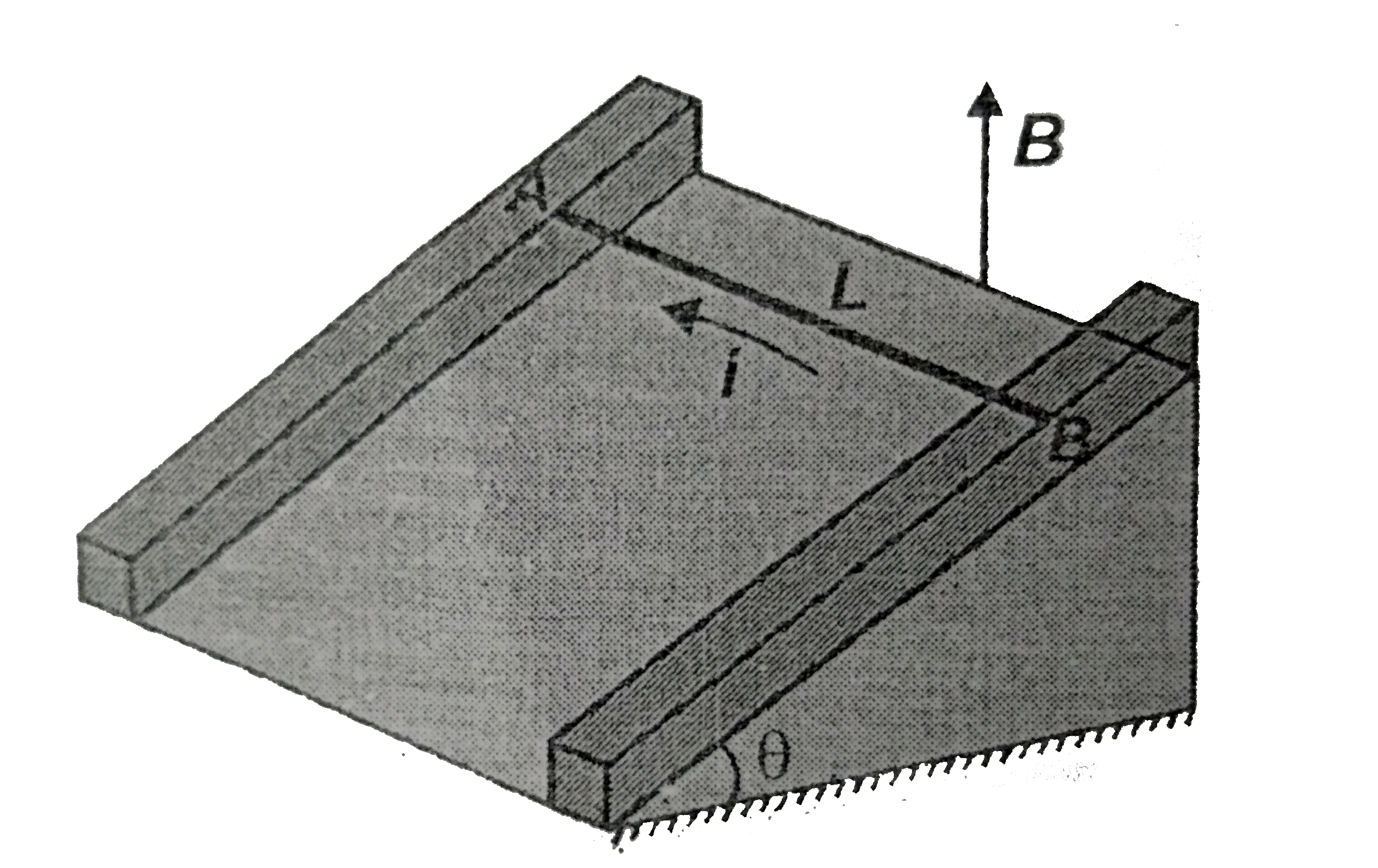
On an inclined plane, two conducting rails are fixed along the line of greatest slope. A conducting rod AB is placed on the radils so that it is horizontal. A vertically upward uniform magnetic field is present in the region. A current i flows through AB from B to A. The mass of AB is m and the coefficient of friction between the rod and rails is μ. Find the minimum and maximum value of B, so that the rod can stay in equilibrium. Assume that μ<tanθ
View Solutionfind out mass of the charge Q, so that it remains in equilibrium for the given configuration.
View Solution
Knowledge Check
Find minimum height of the obstacle so that the shpere can stay in equilibrium
 AR1+cosθBR1+sinθCR(1−sinθ)DR(1−cosθ)
AR1+cosθBR1+sinθCR(1−sinθ)DR(1−cosθ)Find minimum height of the obstacle so that the sphere can stay in equilibrium
 AR1+cosθBR1+sinθCR(1−sinθ)DR(1−cosθ)
AR1+cosθBR1+sinθCR(1−sinθ)DR(1−cosθ)A sphere of density ρ is half submerged in a liquid of density σ and surface tension T. The sphere remains in equilibrium. Find radius of the sphere (assume the force due to surface tension acts tangentially to surface of sphere)
A√T(ρ−σ)gB√T(ρ−2σ)gC√2T(2ρ−3σ)gD√3T(2ρ−σ)g
Find the minimum force F0 that should be applied to the block of mass m = 0.5 kg so that the block stays in equilibrium with the rough vertical wall having friction coefficient μ=0.2 (Take g=10ms2)
View SolutionA sphere of radius R is supported by a rope attached to the wall. The rope makes an angle θ=45∘ with respect to the wall. The point where the rope is attached to the wall is at a distance of 3R2 from the point where the sphere touches the wall. Find the minimum coefficient of friction (μ) between the wall and the sphere for this equilibrium to be possible.
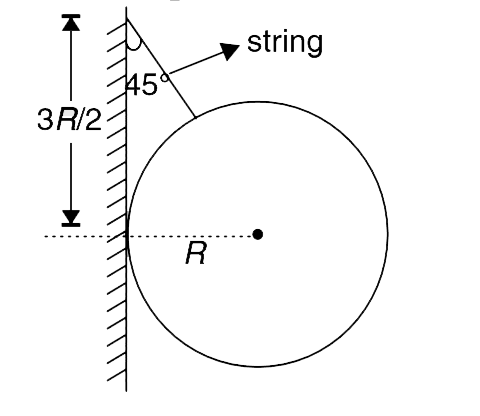
View SolutionThe centre of mass of an inhomogeneous sphere is at a distance of 0.3 R from its geometrical centre. R is the radius of the sphere. Find the maximum inclination (θ) of an incline plane on which this sphere can be placed in equilibrium. Assume that friction is large enough to prevent slipping.
View SolutionFind the minimum height of a mirror where one can see his full image.
View SolutionA hollow sphere of mass 2kg is kept on a rough horizontal surface. A force of 10N is applied at the centre of the sphere as shown in the figure. Find the minimum value of μ so that the sphere starts pure rolling. (take g=10ms−2)

View Solution

