A rod of length L is held vertically on a smooth horizontal surface. T

A rod length L is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At a certain instant of time, when the rod makes an angle $θ$ with horizontal the velocity of COM of the rod is $v_{0}$ . The velocity of the end of the rod in contact with the surface at that instant is:
A $v_{0} cot θ$
B $v_{0} cos θ$
C $v_{0} sin θ$
D $v_{0} tan θ$
A rod of length 1m is sliding in a corner as shown. At an instant when the rod makes an angle of $60^{\circ}$ with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at this instant is :

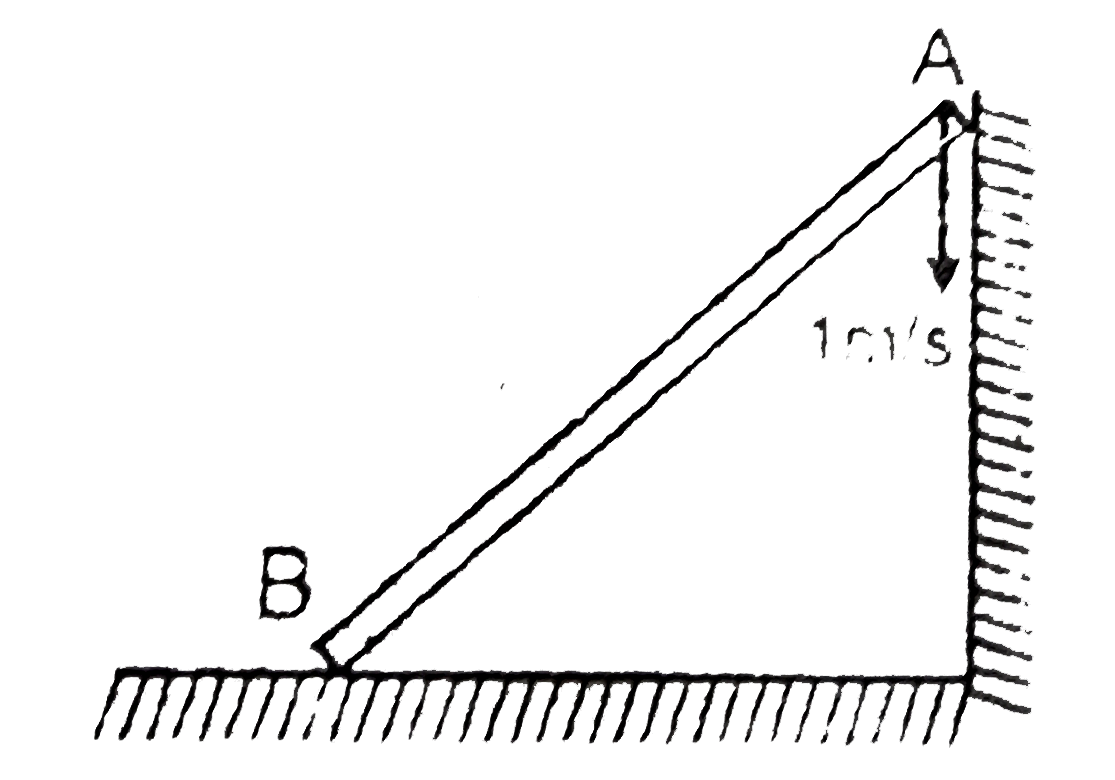A2 rad/s
B1.5 rad/s
C0.5 rad/s
D0.75 rad/s
End $A$ of a rod $A B$ is being pulled on the floor with a constant velocity $v_{0}$ as shown. Taking the length of the rod as $l$ , at an instant when the rod makes an angle $37^{\circ}$ with the horizontal, calculate

the velocity of the $C M$ of the rod
A $\frac{5}{7} v_{0}$ at $\frac{{tan}^{- 1} 4}{3}$ below horizontal
B $\frac{5}{7} v_{0}$ at $\frac{{tan}^{- 1} 3}{4}$ below horizontal
C $\frac{5}{6} v_{0}$ at $\frac{{tan}^{- 1} 3}{4}$ below horizontal
D $\frac{5}{6} v_{0}$ at $\frac{{tan}^{- 1} 4}{3}$ below horizontal

The correct Answer is:D