A U-shaped wire has a semicircular bending between A and B as shown in Fig. A bead of mass m moving with uniform speed v through a wire enters the semicircular bend at A and leaves at B with velocity v/2 after time T. The average force exerted by the bead on the part AB of the wire is

0
3mv2T
3mvT
none of these
The correct Answer is:B
The momentum of the ead at A is Pi−mvˆi
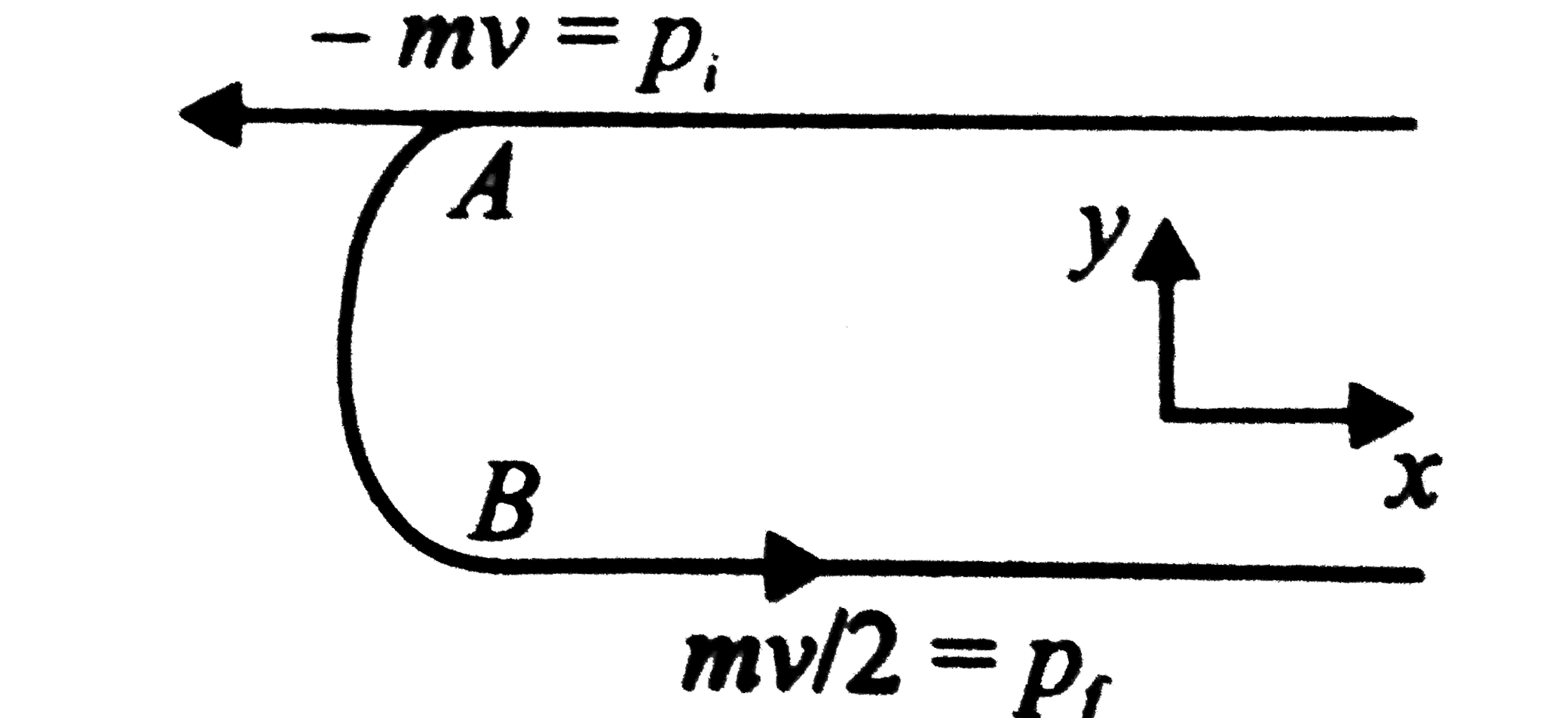
The momentum of the bead at B is →Pf=(mv2)ˆi
Therefore, the magnitude of the change in momentum between A and B is
△P=∣∣→Pf−→Pf∣∣=(32)mv
Average force exerted by the bead on the wire is
Fav=△p△t=3mv2T
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Multiple Correct
Explore 25 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Assertion - Reasoning
Explore 2 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Subjective
Explore 23 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
A U-shaped smooth wire has a semi-circular bending between A and B as shown in fig. A bead of mass m moving with uniform speed v through the wire enters the semiculcular bent at A and leaves at B. Find the average force exerted by the bead on the part AB of the wire.

View SolutionA particle of mass m moves with constant speed v on a circular path of radius r as shown in figure. The average force on it during its motion from A to B is

View Solution
Knowledge Check
A fixed U-shaped smooth wire has a semi-circular bending between A and B as shown in the figure. A bead of mass 'm' moving with uniform speed v through the wire enters the semicircular bend at A and leaves at B. The magnitude of average force exerted by the bead on the part AB of the wire is
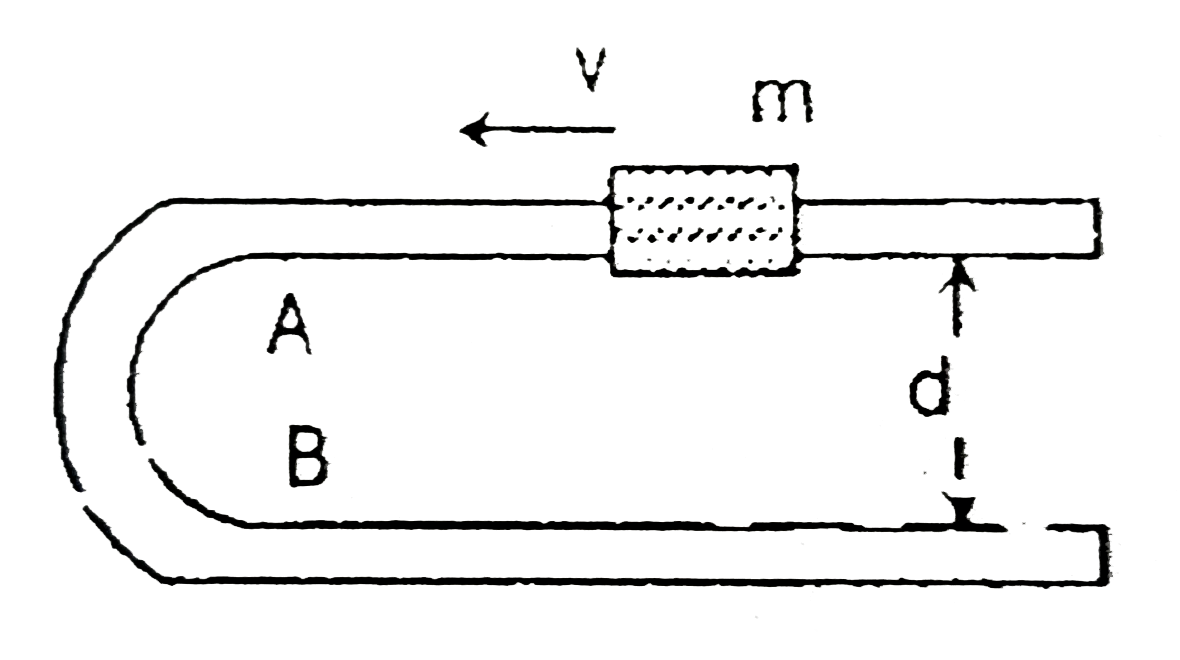 A0B4mv2πdC2mv2πdDNone of these
A0B4mv2πdC2mv2πdDNone of theseConsider a U- shaped fixed smooth wire over which a bead of mass (m) is thrown with speed v.

The bead enters semicircular part at A and leaves at B. What is the magnitude of average force exerted by the bead on the part AB of the wire ?Amv2πdB2mv2πdC4mv2πdD0A semicircular wire of radius R, carrying current I, is placed in a magnetic field as shown in Fig. On left side of X'X, magnetic field strangth 2B0. Both fields are directed inside the page. The magnetic force experienced by the wire would be
 A3IB0RB2IB0RC√10IB0RD√5IB0R
A3IB0RB2IB0RC√10IB0RD√5IB0R
A semicircular wire frame of radius R is standing vertical on a horizontal table. It is pulled horizontally towards right with a constant acceleration. A bead of mass m remain in equilibrium (relative to the semicircular wire) at a position where radius makes an angle q with horizontal. There is no friction between the wire and the bead. The bead is displaced a little bit in upward direction and released. Calculate the speed of the bead relative to the wire at the instant it strikes the table. Assume that all throughout the semicircular wire keeps moving with constant acceleration.
View SolutionFigure 10-82 is an overhead view of semicircular ring of mass m and radius R that lies on a frictionless surface. The ring is connected by elevated spokes (not shown) to a pivot at the center of the semicircle. The ring can rotate around that pivot but is initially stationary. A bead of mass m and speed v is shot into the ring, entering under the spokes and tangentially to the ring and then sliding along the ring. The ring and bead then rotate together around the pivot. Find their angular speed.
View SolutionA bead of mass m stays at point P (a,b) on a wire bent in the shape of a parabola y=4Cx2 and rotating with angular speed ω (see figure ) . The value of ω is (neglect friction),
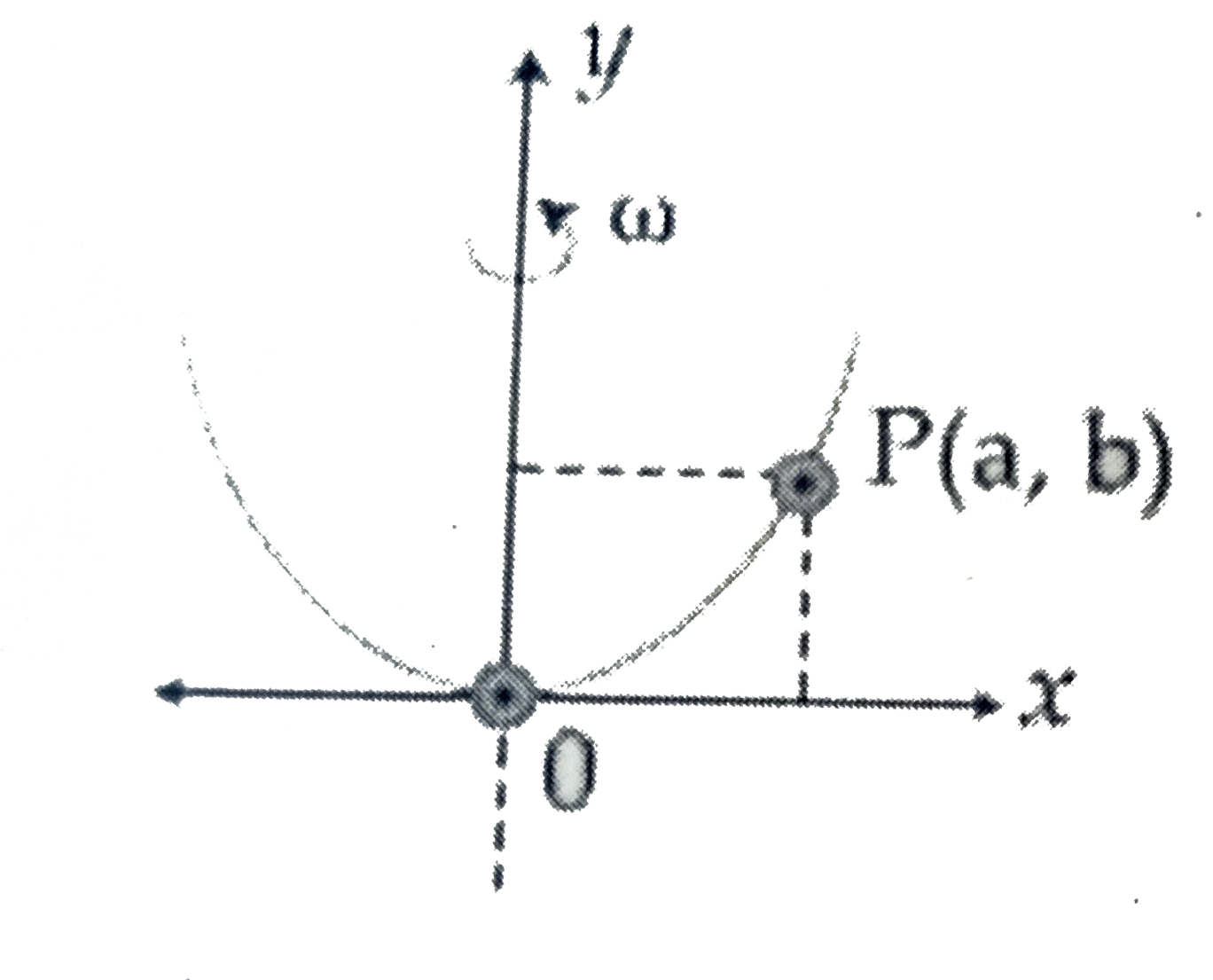
View SolutionA bead of mass m and diameter d is sliding back and forth with velocity v on a wire held between two right walls of length L. Assume that th ecollisions with the wall are perfectly elastic and ther is no friction. The average force that the bouncing bead exerts on the one of the walls is :_
View SolutionThe wires A and B shown in Fig. are made of the same material and have radii rA and rB, respectively. The block between them has a mass m. When the force F is mg/3, one of the wires breaks. Then

View Solution

