Two identical balls, of equal masses A and B, are lying on a smooth surface as shown in Fig. Ball A hits ball B (which is at rest) with a velocity v=16m/s. What should be the minimum value of coefficient of restitution between A and B so that B just reaches the highest point of inclined plane?

23
14
12
13
The correct Answer is:B
v=16m/s

Let velocity of B after collision be v2 and that of A be v1. Then
v≡√2gh=√2×10×5=10m/s
mv1+mv2=mv
v1+10=16⇒v1=6m/s
e=v2−v1v=10−616=14
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Multiple Correct
Explore 25 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Assertion - Reasoning
Explore 2 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Subjective
Explore 23 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
Two identical balls A and B lie on a smooth horizontal surface, which gradually merges into a curve to a height 3.2m. Ball A is given a velocity of 10m/s, to collide head-on with ball B, which then takes up the curved path. What is the minimum coefficient of restitution, e, for the collision between A and B in order that ball B reaches the highest point C of the curve.

View SolutionTwo identical balls A and B are moving as shown in the fig. Ball A hits a smooth floor head on with a velocity u and at the same instant ball B strikes A head on with a horizontal velocity u. The collision between A and B is perfectly inelastic whereas the coefficient of restitution for collision between A and the floor is e=0.5. At what time the two balls will collide again? Assume friction to be absent everywhere.
View Solution
Knowledge Check
Two identical balls of equal masses A and B , are lying on a smooth surface as shown in figure Ball A hits the ball B (which is at rest) with a velocity v=16m/s What should be the minimum value of coefficient of restitution e beteeen A and B so that B just reaches the highest point of inclined plane:
(Takeg=10m/s2)
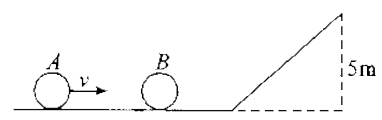 A23B14C12D13
A23B14C12D13Two identical balls of equal masses A and B, are lying on a smooth surface as shown in the figure. Ball A hits the ball B (which is at rest) with a velocity v=16ms−1. What should be the minimum value of coefficient of restitution e between A and B so that B just reaches the highest point of inclined plane? (g=10ms−2)
 A(a) 23B(b) 14C(c) 12D(d) 13
A(a) 23B(b) 14C(c) 12D(d) 13A ball of mass moving with a velocity u collides head on with a ball B of mass m at rest. If the coefficient of restitution is e. the ratio of final velocity of B to the initial velocity of A is
A1−e1+eB1+e1−eC1+e2D1−e2
A ball of mass 2m impinges directly on a ball of mass m, which is at rest. If the velocity with which the larger ball impinges be equal to the velocity of the smaller mass after impact then the coefficient of restitution :-
View SolutionTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

View SolutionA glass ball collides with a smooth horizontal surface (xz plane) with a velocity V=ai−bj. If the coefficient of restitution of collision be e, the velocity of the ball just after the collision will be
View SolutionBall 1 collides with an another identical ball 2 at rest as shown in figure. For what value of coefficient of restitution e, the velocity of ball 2 becomes two times that of ball I after collision?
View SolutionA ball of mass 2m impinges directly on a ball of mass m, which is at rest. If the velocity with which the larger ball impringes be equal to the velocity of the smaller mass after impact then the coefficient of restitution :-
View Solution

