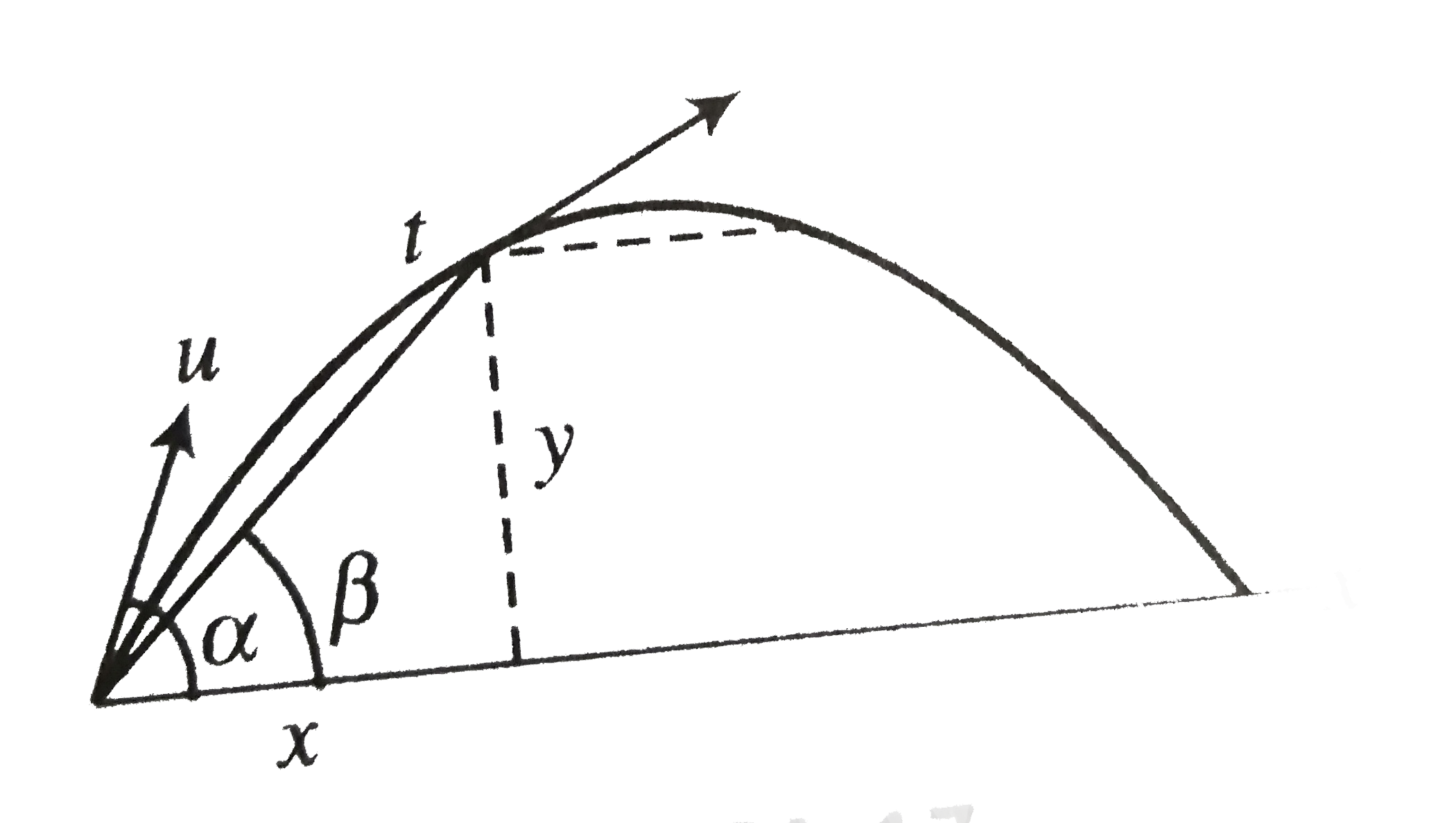
A particle is projected at an angle of elevation α and after t second it appears to have an elevation of β as seen from the point of projection. Find the initial velocity of projection.
gt2sin(α−β)
gtcosβ2sin(α−β)
sin(α−β)2gt
2sin(α−β)gtcosβ
The correct Answer is:B
b. yx=tanβ
⇒usinαt−12gt2ucosαt=tanβ
or usinα−tanβucosα=gt2oru=>cosβ2sin(α−β).
 .
.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Multiple Correct Answer Type
26 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
A particle is projected from a point on the level ground and its height is h when at horizontal distances aand2a from its point of projection. Find the velocity of projection.
View SolutionIf an object is thrown at an angle of 60∘ with horizontal, find elevation angle of the object at its highest point as seen from the point of projection.
View Solution
Knowledge Check
A particle I projected at an angle of elevation α after time t it makes an angle βwith horizontal. The velocity of projection is
A2gtcosβsin(α−β)Bgtcosβsin(α−β)Cgt2sin(α−β)D4gtsin(α−β)A particle is projected at an angle θ with the horizontal . If angle of elevation of highest point of trajectory is ϕ when seen from point of projection, then
Atanϕ=2tanϕBtanθ=3tanϕCtanθ=2tanϕDtanθ=4tanϕA projectile is fired at an angle of 45∘ with the horizontal. Elevation angle of the projection at its highest point as seen from the point of projection is
A60∘Btan−1(12)Ctan−1(√32)D45∘
A ball is projected from ground in such a way that after 10 seconds of projection it lands on ground 500 m away from the point of projection. Find out :-
(i) angle of projection
(ii) velocity of projection
(iii) Velocity of ball after 5 seconds
View SolutionA particle is projected from the ground with an initial speed v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectory is [EAM2013]
View SolutionA particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View SolutionA particle is projected from ground with speed u and at an angle θ with horizontal. If at maximum height from ground, the speed of particle is 1/2 times of its initial velocity of projection, then find its maximum height attained.
View Solution
