A ball is projected from ground in such a way that after 10 seconds of projection it lands on ground 500 m away from the point of projection. Find out :-
(i) angle of projection
(ii) velocity of projection
(iii) Velocity of ball after 5 seconds
The correct Answer is:(i)θ=45∘
(ii)50√2m/s
(iii)50m/sec
To solve the problem step by step, we will use the equations of projectile motion.
Given:
- Time of flight (T) = 10 seconds
- Horizontal distance (Range, R) = 500 m
- Acceleration due to gravity (g) = 9.8 m/s²
Step 1: Find the Horizontal and Vertical Components of Velocity
The horizontal range (R) of a projectile is given by the formula:
R=ucos(θ)⋅T
Where:
- u = initial velocity
- θ = angle of projection
- T = time of flight
Rearranging the formula to find ucos(θ):
ucos(θ)=RT=500m10s=50m/s
Step 2: Find the Vertical Component of Velocity
The time of flight for a projectile is given by:
T=2usin(θ)g
From this, we can express usin(θ):
usin(θ)=gT2=9.8m/s2⋅10s2=49m/s
Step 3: Find the Angle of Projection
Now, we have two equations:
1. ucos(θ)=50m/s
2. usin(θ)=49m/s
To find tan(θ):
tan(θ)=usin(θ)ucos(θ)=4950
Now, we can find θ:
θ=tan−1(4950)
Calculating this gives:
θ≈44.42∘
Step 4: Find the Velocity of Projection
Now we can find the initial velocity u using the Pythagorean theorem:
u=√(ucos(θ))2+(usin(θ))2
u=√(50)2+(49)2=√2500+2401=√4901
Calculating this gives:
u≈70m/s
Step 5: Find the Velocity of the Ball after 5 seconds
After 5 seconds, the vertical component of the velocity will be:
vy=usin(θ)−gt=49m/s−9.8m/s2⋅5s
vy=49m/s−49m/s=0m/s
The horizontal component of the velocity remains constant:
vx=ucos(θ)=50m/s
Thus, the resultant velocity after 5 seconds is:
v=√(vx)2+(vy)2=√(50)2+(0)2=50m/s
Summary of Results:
(i) Angle of projection θ≈44.42∘
(ii) Velocity of projection u≈70m/s
(iii) Velocity of the ball after 5 seconds v≈50m/s
- Time of flight (T) = 10 seconds
- Horizontal distance (Range, R) = 500 m
- Acceleration due to gravity (g) = 9.8 m/s²
R=ucos(θ)⋅T
Where:
- u = initial velocity
- θ = angle of projection
- T = time of flight
ucos(θ)=RT=500m10s=50m/s
T=2usin(θ)g
usin(θ)=gT2=9.8m/s2⋅10s2=49m/s
1. ucos(θ)=50m/s
2. usin(θ)=49m/s
tan(θ)=usin(θ)ucos(θ)=4950
θ=tan−1(4950)
θ≈44.42∘
u=√(ucos(θ))2+(usin(θ))2
u=√(50)2+(49)2=√2500+2401=√4901
u≈70m/s
vy=usin(θ)−gt=49m/s−9.8m/s2⋅5s
vy=49m/s−49m/s=0m/s
vx=ucos(θ)=50m/s
v=√(vx)2+(vy)2=√(50)2+(0)2=50m/s
(i) Angle of projection θ≈44.42∘
(ii) Velocity of projection u≈70m/s
(iii) Velocity of the ball after 5 seconds v≈50m/s
Topper's Solved these Questions
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (NEWTONS LAWS OF MOTION)
Explore 44 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (FRICTION)
Explore 11 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Units, Dimensions & Measurements)
Explore 33 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
Similar Questions
Knowledge Check
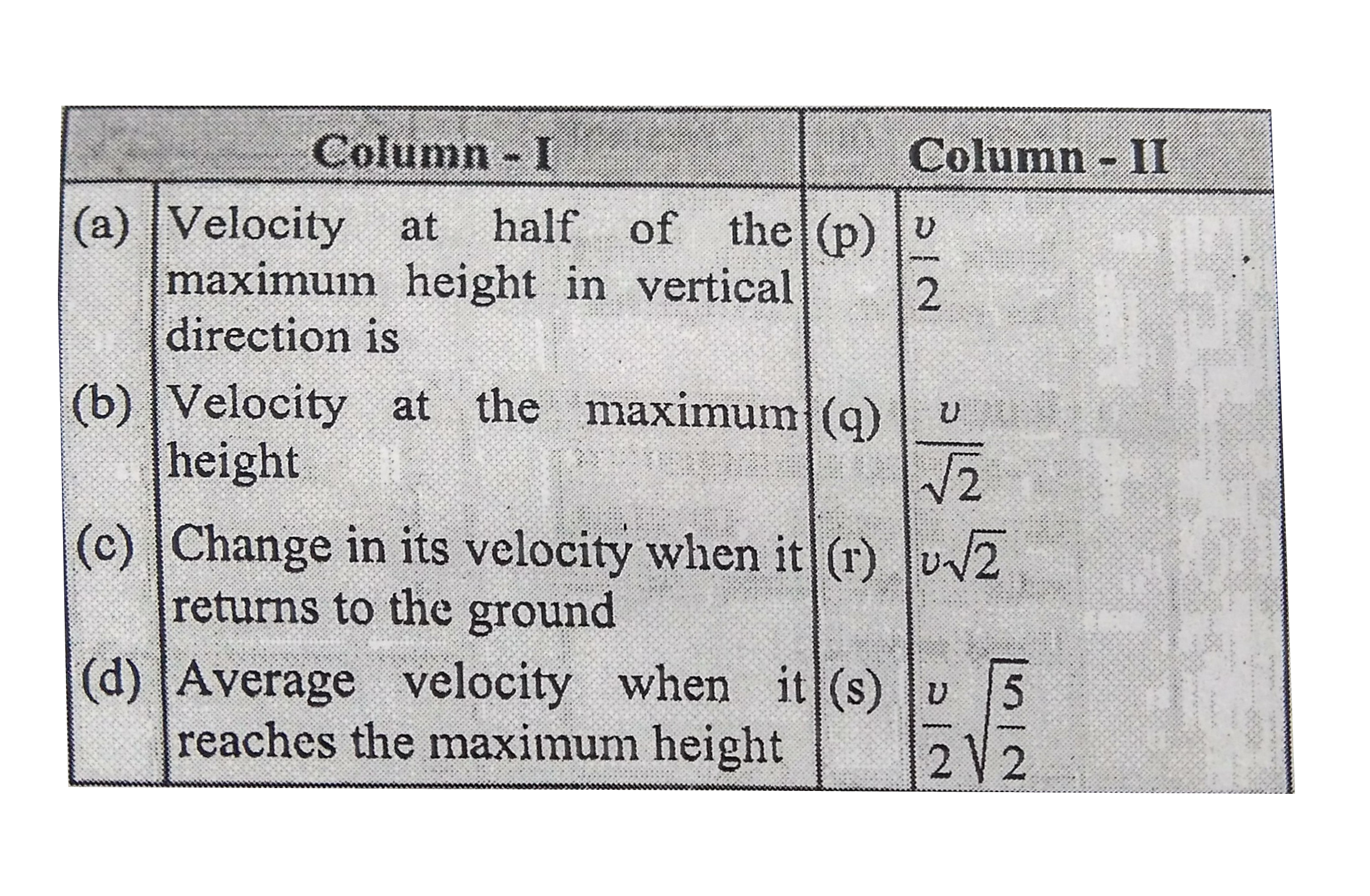
A ball is projected from the ground with velocity u such that its range is maximum Then
AIts velocity at half the maximum height is √32uBIts velocity at the maximum height is uCChange in its velocity when it returns to the ground is uDall the above are trueA particle just clear a wall of height b at a distance a and strikes the ground at a distance from the point of projection, the angle of projection is :
Atan−1(bac)B45∘Ctan−1(bca(c−1))Dtan−1(bca)A ball is projected horizontally. After 3s from projection its velocity becomes 1.25 times of the velocity of projection. Its velocity of projection is
A10 m/sB20 m/sC30 m/sD40 m/s
A particle is projected at an angle of elevation α and after t second it appears to have an elevation of β as seen from the point of projection. Find the initial velocity of projection.
View SolutionA ball is thrown from a comer of room of length 20 m and height 5 m such that the ball moves along the length of room just touching the ceiling and drops on the other corner. Find out
(i) Angle of projection
(ii) Velocity of projection
(iii) Time of flight
View SolutionA body projected just crosses a wall of 4m height,at 6m distance from the point of projection and it hits the ground at 12m away from the wall. The angle of projection is nearly
View SolutionA ball is thrown from the ground to clear a wall 3 m high at a distance of 6 m and falls 18 m away from the wall. Find the angle of projection of ball.
View SolutionA particle projected from ground moves at angle 45∘ with horizontal one second after projection and speed is minimum two seconds after the projection The angle of projection of particle is [ Neglect the effect of air resistance )
View Solution