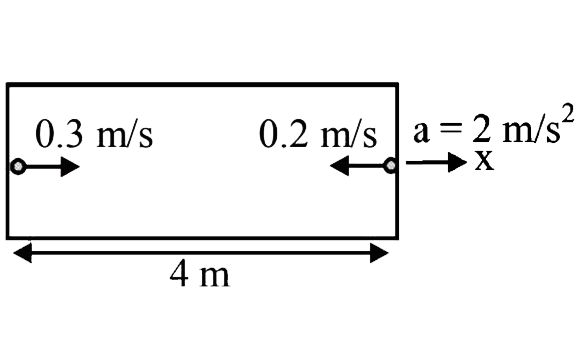
A rocket is moving in a gravity free space with a constant acceleration of 2m/s2 along +x direction (see figure). The length of a chamber inside the rocket is 4m. A ball is thrown from the left end of the chamber in +x direction with a speed of 0.3m/s relative to the rocket . At the same time , another ball is thrown in +x direction with a speed of 0.2m/s drom its right end relative to the rocket . The time in seconds when the two balls hit each other is
The correct Answer is:2
Consider motion of two balls with respect to rocket
Maximum distance of ball A from left wall
u22a=0.3×0.32×2=0.094≈0.02m
So collision of two balls will take place very near to left wall
For BS=ut+12at2
−4=−0.2t−(12)2t2⇒t2+0.2t−4=0
⇒t=−0.2±√0.04+162=1.9
nearest integer = 2s.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - True or False
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
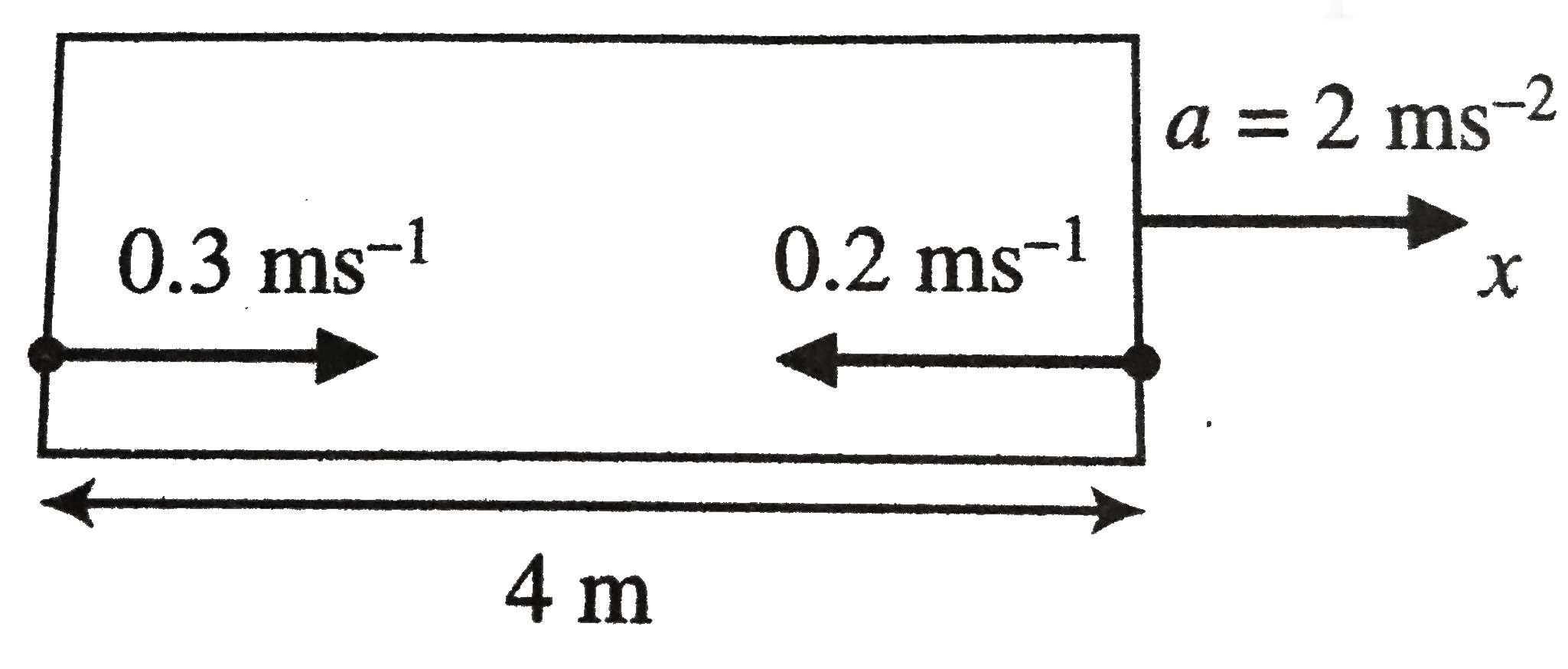
A rocket is moving in a gravity free space with a constant acceleration of 2ms−1 along +x direction (see Fig.5.126). The length of a chamber inside the rocket is 4m. A ball is thrown from the left end of the chamber in +x direction with a speed of 0.3 ms−1 relative to the rocket. At the same time , another ball is thrown in -x direction with a speed of 0.2ms−1 from its right and relative to the rocket. the time in seconds when the two balls hit each other is:

View SolutionA ball is dropped from the top of a tower. After 2s another ball is thrown vertically downwards with a speed of 40m/s. After how much time and at what distance below the top of tower the balls meet?
View Solution
Knowledge Check
A ball is thrown horizontally with a speed of 20m/s from the top of a tower of height 100m
Time taken by the ball to strike the ground isA√20sB2√20sC4√20sD10sA particle (A) is dropped from a height and another particles (B) is thrown into horizontal direction with speed of 5m/s sec from the same height. The correct statement is
ABoth partiles will reaches at ground simultaneouslyBBoth particles will reaches at ground with the same speedCParticle (A) will reach at ground at first with respect to particle (B)DParticle (B) will reach at ground at first with respect to particle (A)A ball is dropped from the top of a building of height 80 m. At same instant another ball is thrown upwards with speed 50 m/s from the bottom of the building. The time at which balls will meet is
A1.6 sB5 sC8 sD10 s
A ball is thrown up at a speed of 4.0 m/s. Find the maximum height reached by the ball. Take g=10m/s2.
View SolutionA ball A is dropped from a building of height 45m. Simultaneously another ball B is thrown up with a speed 40m/s. Calculate the relative speed of the balls as a function of time.
View SolutionA ball is thrown in upwards direction then the force(s) acting on it is (are)
View SolutionA ball is thrown in upwards direction then the force(s) acting on it is (are)
View SolutionA cricket ball is thrown at a speed of 30 m s−1 in a direction 30∘ above the horizontal. The time taken by the ball to return to the same level is
View Solution
