Two particles A and B are placed as shown in figure. The particle A, on the top of tower, is projected horizontally with a velocity u and particle B is projected along the surface towards the tower, simultaneously. If both particles meet each other, then the speed of projection of particles B is [ignore any friction]
![Two particles A and B are placed as shown in figure. The particle A, on the top of tower, is projected horizontally with a velocity u and particle B is projected along the surface towards the tower, simultaneously. If both particles meet each other, then the speed of projection of particles B is [ignore any friction]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V01_MAA_E01_028_Q01.png)
d√g2H−u
d√g2H
d√g2H+u
u
The correct Answer is:A
a. Time taken by particles to collide
t=√2Hg
Then u√2Hg+V√2Hg=d
⇒u+V=d√g2Horv=d√g2H−u.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Multiple Correct Answer Type
26 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
A particle is projected vertically upwards and t second after another particle is projected upwards with the same initial velocity. Prove that the particles will meet after a lapse of (t2+ug) time from the instant of projection of the first particle.
View SolutionA particle is projected along an inclined plane as shown in figure. What is the speed of the particle when it collides at point A ? (g=10m/s)

View Solution
Knowledge Check
A particle is projected horizontally from a tower with velocity u towards east. Wind provides constant horizontal acceleration g2 towards west. If particle strikes the ground vertically the then :
 AHeight of toward is 2u2gBThe speed with which particle strikes ground is 2uCWork done by wind force 12μ2DParticle3 strikes the ground after time t=2u/g
AHeight of toward is 2u2gBThe speed with which particle strikes ground is 2uCWork done by wind force 12μ2DParticle3 strikes the ground after time t=2u/gAssertion Particle-1 is dropped from a tower and particle-2 is projected horizontal from the same tower. Then both the particles reach the ground simultaneously.
Reason Both are particles strike the ground with different speeds.AIf both Asseration and Reason are correct and Reason is the correct explanation of AssertionBIf both Assertion and Reason are correct but Reason is not the correct explanation of AssertionCIf Assertion is true but Reason is falseDIf Assertion is false but Reason is trueTwo particles A and B are projected simultaneously from a fixed point of the ground. Particle A is projected on a smooth horizontal surface with speed v, while particle B is projected in air with speed v, while particle B is projected in air with speed 2v√3. If particle B hits the particle A, the angle of projection of B with the vertical is
A30∘B60∘CBoth (a) and (b)D45∘
Two particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then :
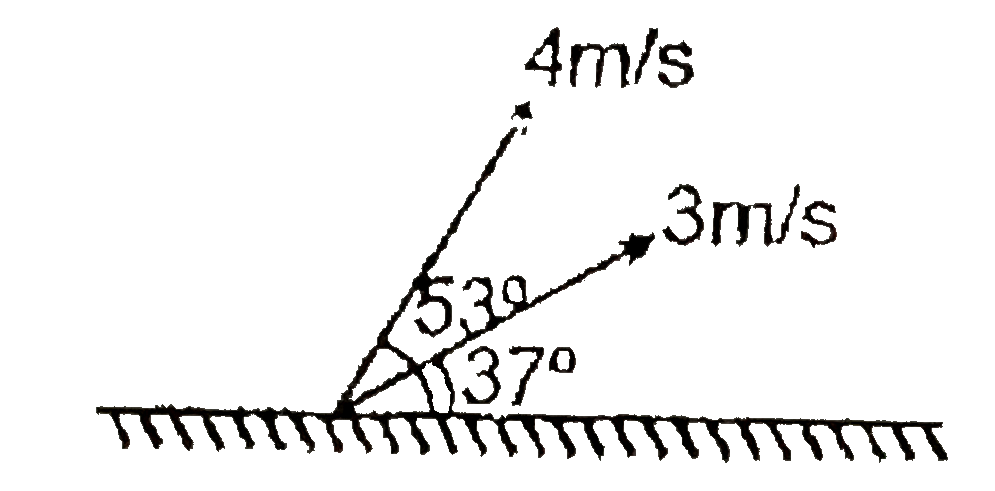
View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View SolutionTwo particles A and B projected simultaneously from a point situated on a horizontal place. The particle A is projected vertically up with a velcity vA while the particle B is projected up at an angle 30∘ with horizontal with velocity vB. After 5s the particles were observed moving mutually perpendicular to each other. The velocity of projection of the particle vAandvB respectively are:
View SolutionA particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
View SolutionTwo particles A and B having different masses arc projected from a tower with same speed. A is projected vertically upward and B vertically downward. On reaching the ground
View Solution
