A solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
11GMmR2
14GMmR2
GMm2R2
GMmR2
The correct Answer is:B
To calculate the force of attraction on the point mass m we should calculate the force due to the solid spere and substract from this force which the mass o fhte hollow sphere would have exerted on m
F=GmMx2−GmMy2[∴=R/4x+y=R/2]

M=(43)πR3P
and M=43πR(2)3p=M8
=14GmMR2
Topper's Solved these Questions
- GRAVITATION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - GRAVITATION EXERCISE - MHT CET Corner
20 Videos
- GRAVITATION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - GRAVITATION EXERCISE - Exercise 1
69 Videos
- FRICTION IN SOLID AND LIQUIDSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FRICTION IN SOLID AND LIQUIDSEXERCISE - EXERCISE 2 (Miscellaneous Problems)
24 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHT BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHT EXERCISE - MHT CET Corner
24 Videos
Similar Questions
A fixed sphere of radius R and uniform density ρ has a spherical cavity of radius R/2 such that the surface of the cavity passes through the centre of the sphere. A particle of mass m is located at the centre (A) of the velocity. Calculated
(a) The gravitational field at A.
(b) The velocity with which the particle strikes the centre O of the sphere. (Neglect earth's gravity)
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View Solution
Knowledge Check
The figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is
 Anon - uniformBtowards the center of the cavityCdirectly proportional to aDAll of these
Anon - uniformBtowards the center of the cavityCdirectly proportional to aDAll of theseA mass m is placed in the cavity inside hollow sphere of mass M as shown in the figure. The gravitational force on m is
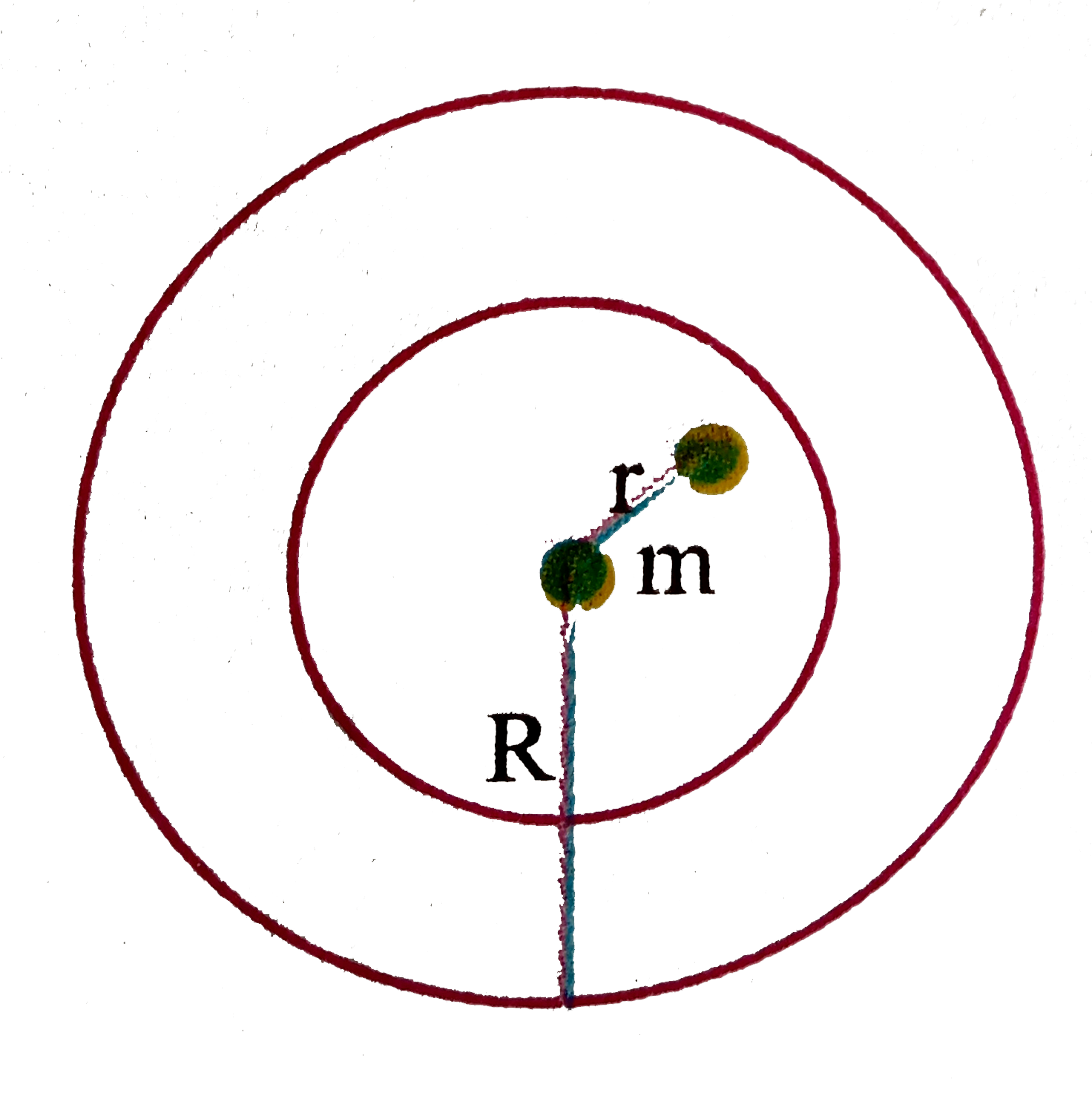 AGMmR2BGMmr2CGMm(R−r)2Dzero
AGMmR2BGMmr2CGMm(R−r)2DzeroInside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
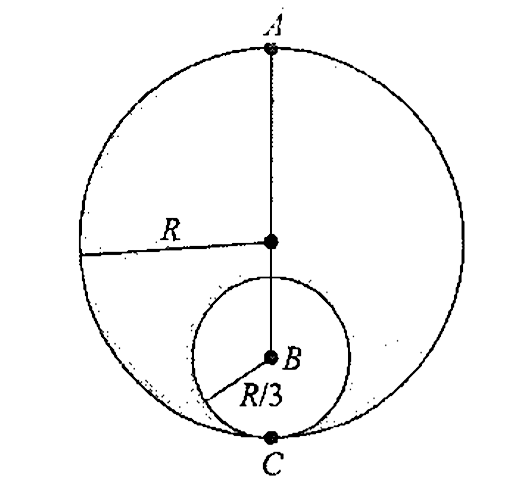 AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system only
AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system only
The potential at a distance R/2 from the centre of a conducting sphere of radius R will be
View SolutionA point mass m0 is placed at distance R/3 from the centre of spherical shell of mass m and radius R. the gravitational force on the point mass m0 is
View SolutionA mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass M is
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solid sphere]
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of mass m at a distance R/2 from the centre of the sphere on the line joining both the centre of the cavity)
[Here g=(GM)/R2, where M is the mass of the sphere
View Solution
