Question

Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is

Options

A. `(Gm)/(R )`
B. `sqrt(2sqrt(2)(GM)/(R )`
C. `sqrt(GM)/(R )(2sqrt(2)+1)`
D. `sqrt(GM)/(R )(2sqrt(2)+1)/(4)`

Answer

D

Explanation

To find the speed of each particle moving in a circle of radius $$R$$ under the action of their mutual gravitational attraction, we can follow these steps:

Step 1: Understand the System
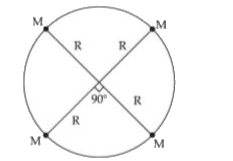
We have four particles, each of mass \( M \), moving in a circle of radius \( R \). The gravitational attraction between these particles provides the necessary centripetal force for circular motion.

Step 2: Calculate the Gravitational Force
The gravitational force \( F \) between two particles is given by Newton's law of gravitation:
\( F = \frac{G M^2}{d^2} \)
where \( G \) is the gravitational constant and \( d \) is the distance between the two particles.

Step 3: Determine the Distances
In a square configuration (since there are four particles), the distance between any two adjacent particles is \( R \), and the distance between diagonally opposite particles is \( \sqrt{2}R \).

Step 4: Calculate the Net Gravitational Force on One Particle
For one particle, the net gravitational force will be the vector sum of the forces exerted by the other three particles.

1. The force from each adjacent particle (2 particles) at distance \( R \):
\( F_{adjacent} = \frac{G M^2}{R^2} \)
There are two such forces.

2. The force from the diagonally opposite particle (1 particle) at distance \( \sqrt{2}R \):
\( F_{diagonal} = \frac{G M^2}{(\sqrt{2}R)^2} = \frac{G M^2}{2R^2} \)

Step 5: Calculate the Total Force
The total gravitational force acting on one particle can be expressed as:
\( F_{net} = 2F_{adjacent} + F_{diagonal} = 2\left(\frac{G M^2}{R^2}\right) + \frac{G M^2}{2R^2} \)
Combining these:
\( F_{net} = \frac{2G M^2}{R^2} + \frac{G M^2}{2R^2} = \frac{4G M^2}{2R^2} + \frac{G M^2}{2R^2} = \frac{5G M^2}{2R^2} \)

Step 6: Relate the Net Force to Centripetal Force
For circular motion, the net gravitational force provides the centripetal force required to keep the particle moving in a circle:
\( F_{net} = \frac{M v^2}{R} \)
Setting the two expressions for force equal gives:
\( \frac{5G M^2}{2R^2} = \frac{M v^2}{R} \)

Step 7: Solve for Velocity \( v \)
Rearranging the equation to solve for \( v^2 \):
\( v^2 = \frac{5G M}{2R} \)
Taking the square root gives:
\( v = \sqrt{\frac{5G M}{2R}} \)

Final Answer
The speed of each particle is:
\( v = \sqrt{\frac{5G M}{2R}} \)