A long block A is at rest on a smooth horizontal surface. A small block B whose mass is half of mass of A is placed on A at one end and is given an initial velocity u as shown in figure. The coefficient of friction between the blocks is μ.
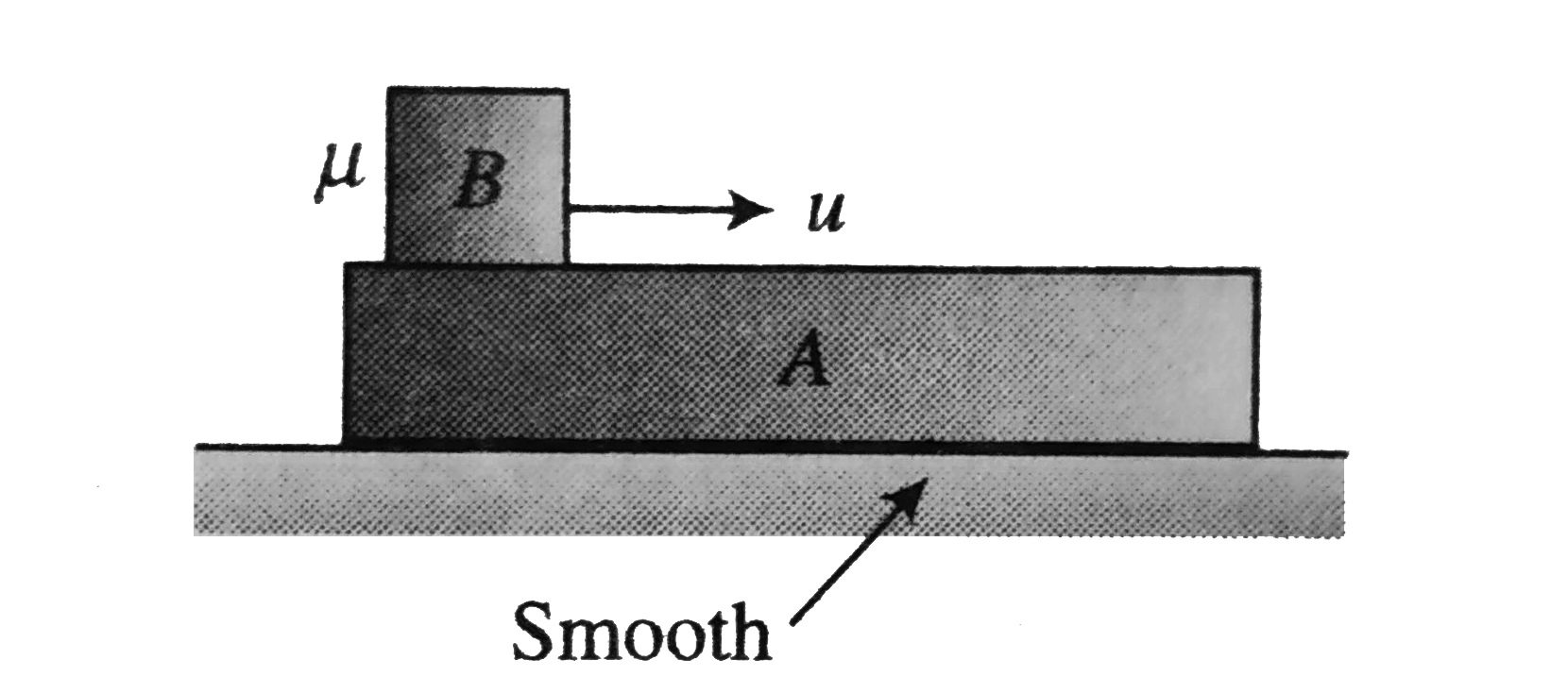
(a) Finally both move with a common velocity 2u/3.
(b) Acceleration of B relative to A initially is 3μg/2 towards left.
(c) Magnitude of total work done by friction is equal to the final kinetic energy of the system.
(d) The ratio of initial to final momentum of the system is 1.
The correct Answer is:B, D
v is the final common velocity.

(m+2m)v=mu⇒v=u3

a1=μmgm=μg,a2=μmg2m=μg2
Acceleration of B relative to A:
a1+a2=μg+μg2=32μg towards left
Work done against friction:
W1=Ki−Kf=12mu2−123mv2=mu23
Final KE=123mv2=mu26
Hence, c. is not correct.
Option (d) is correct, because momentum is always conserved as there is no external force.
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Linked Comprehension
Explore 55 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Integer
Explore 14 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Single Correct
Explore 100 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
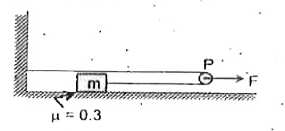
A block of mass m = 2kg is accelerating by a force F = 20N applied on a smooth light pulley as shown in the figure. If the coefficient of kinetic friction between the block and the surface is μ=0.3, find its acceleration.
View SolutionA rectangular block is kept on a rough horizontal surface and given some initial velocity. The coefficient of friction between the block and the surface is constant. The block will topple
View Solution
Knowledge Check
A long block A is at rest on a smooth horizontal surface. A small block B, whose mass is half of A, is placed on A at one end and projected along A with some velocity u. The coefficient of friction between the blocks is μ:
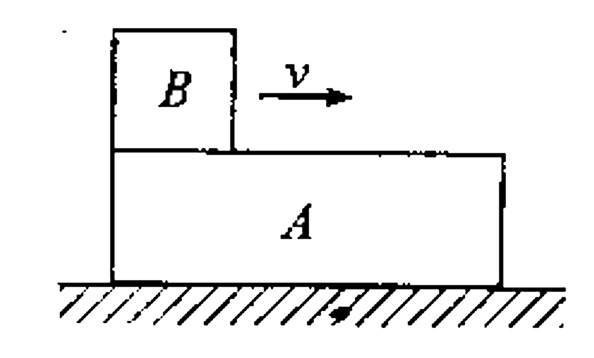 AThe blocks will reach the final common velocity u3Bthe work done against friction is two-thirds of the initial kinetic energy of BCbefore the block reach a common velocity the acceleration of A relative to B is 23μg.DBefore the blocks reach a common velocity the acceleration of A relative to B is 32μg.
AThe blocks will reach the final common velocity u3Bthe work done against friction is two-thirds of the initial kinetic energy of BCbefore the block reach a common velocity the acceleration of A relative to B is 23μg.DBefore the blocks reach a common velocity the acceleration of A relative to B is 32μg.A long block A of mass M is at rest on a smooth horizontal surface.A small block B of mass M/2 is placed on A at one end and projected along A with some veklocity v.The coefficient of friction between the block is μ then , the accelerations of blocks A and B before reaching a common velocity will be respectively
 Aμg2(towards right),μg2(towards left)Bμg2(towards right),(μg)(towrards left)Cμg2(towards right),(μg)(towrards left)D(μg)(towards right),μg2(towrards left)
Aμg2(towards right),μg2(towards left)Bμg2(towards right),(μg)(towrards left)Cμg2(towards right),(μg)(towrards left)D(μg)(towards right),μg2(towrards left)A block of mass 1 kg is placed on a wedge shown in figure. Find out minimum coefficient of friction between wedge and block to stop the block on it.
 A0.6B0.9C1D0.2
A0.6B0.9C1D0.2
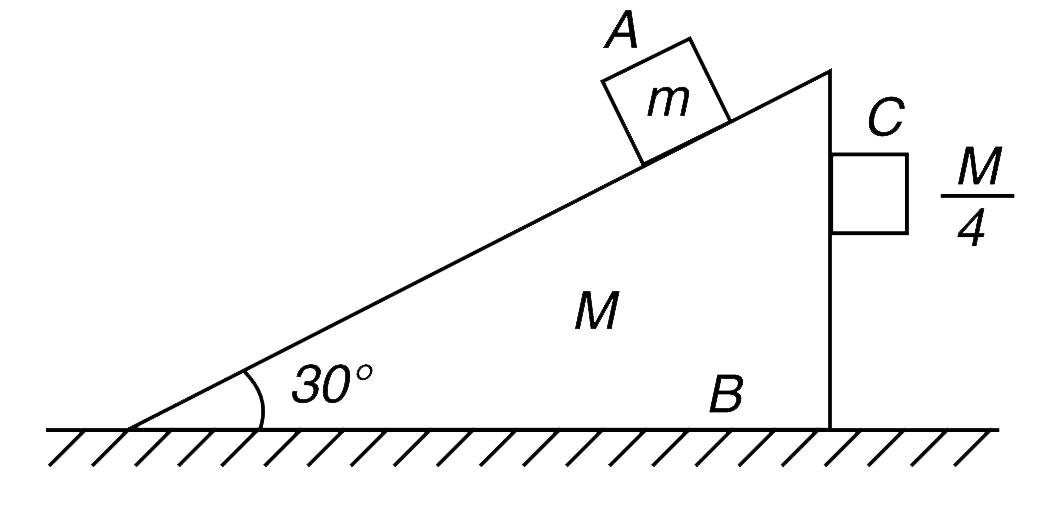
In the arrangement shown in figure, a block A of mass m has been placed on a smooth wedge B of mass M. The wedge lies on a horizontal smooth surface. Another block C of mass M4 has been placed in contact with the wedge B as shown. The coefficient of friction between the block C and the vertical wedge wall is μ=34. Find the ratio mM for which the block C will not slide with respect to the wedge after the system is released?
View SolutionA small block of mass 'm' is placed on a plank of mass 'M'. The block is connected to plank with the help of a light string passing over a light smooth pulley as shown in figure. The co-efficient of static friction between the block and plank is μ.
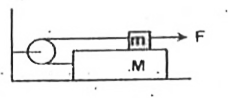
The co-efficient of friction between the plank and the horizontal surface is zero. What maximum horizontal force F applied on the block of mass m can make the block and plank not to slide relatively?
View SolutionA sufficiently long plane of mass 4kg is placed on a smooth horizontal surfaces A small block of mass 2kg is placed over the plank and is beging acted upon by a time verying horizontal force F=(0.5t) where F is in newton and t is in second as shown in figure. The coefficient of friction slipping the plank and the block is given is μs=μk=μ time t=12s the relative slipping between the plank and the block is just likely to accor

The coefficient of friction μ is equal to
View SolutionA block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
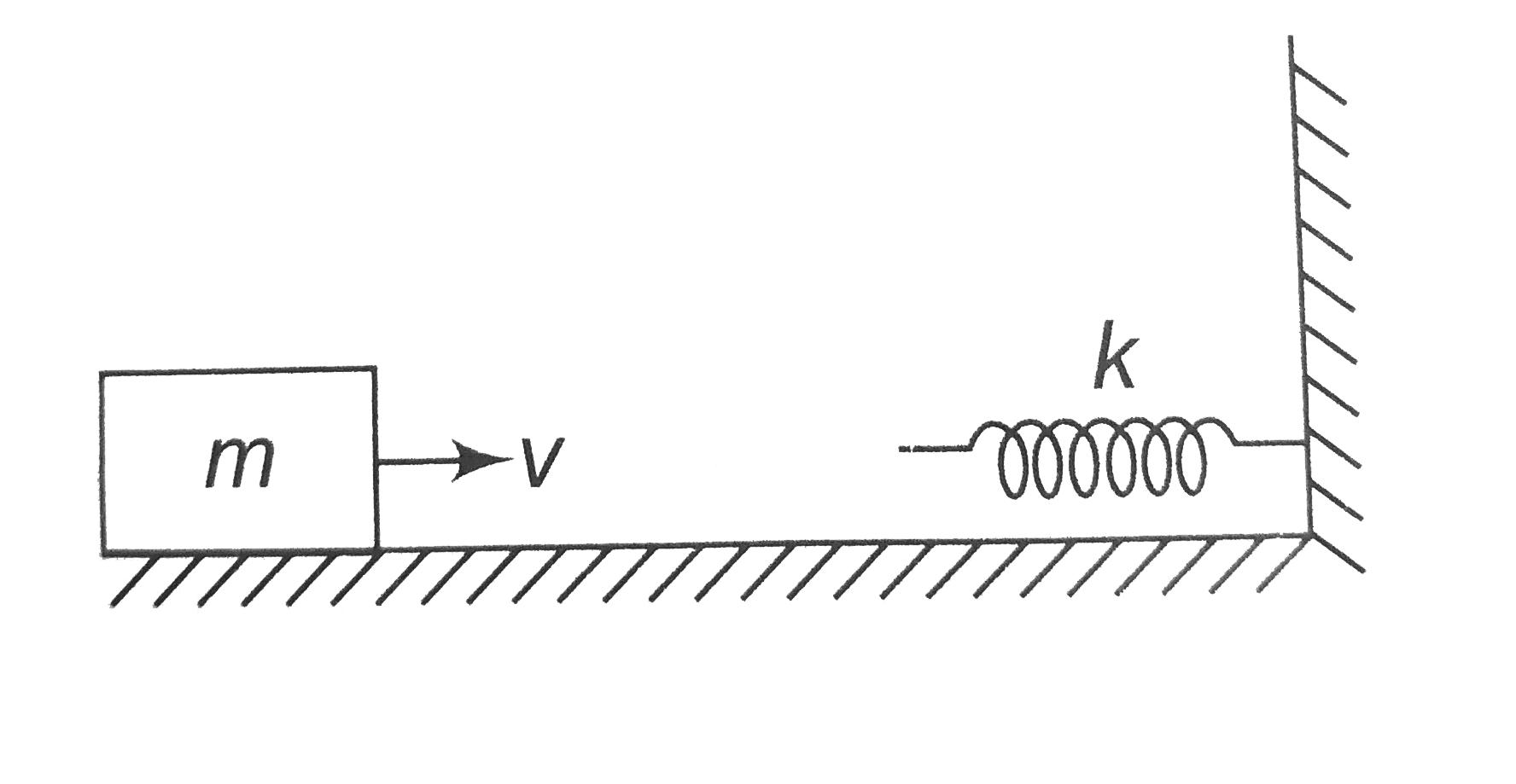
View Solution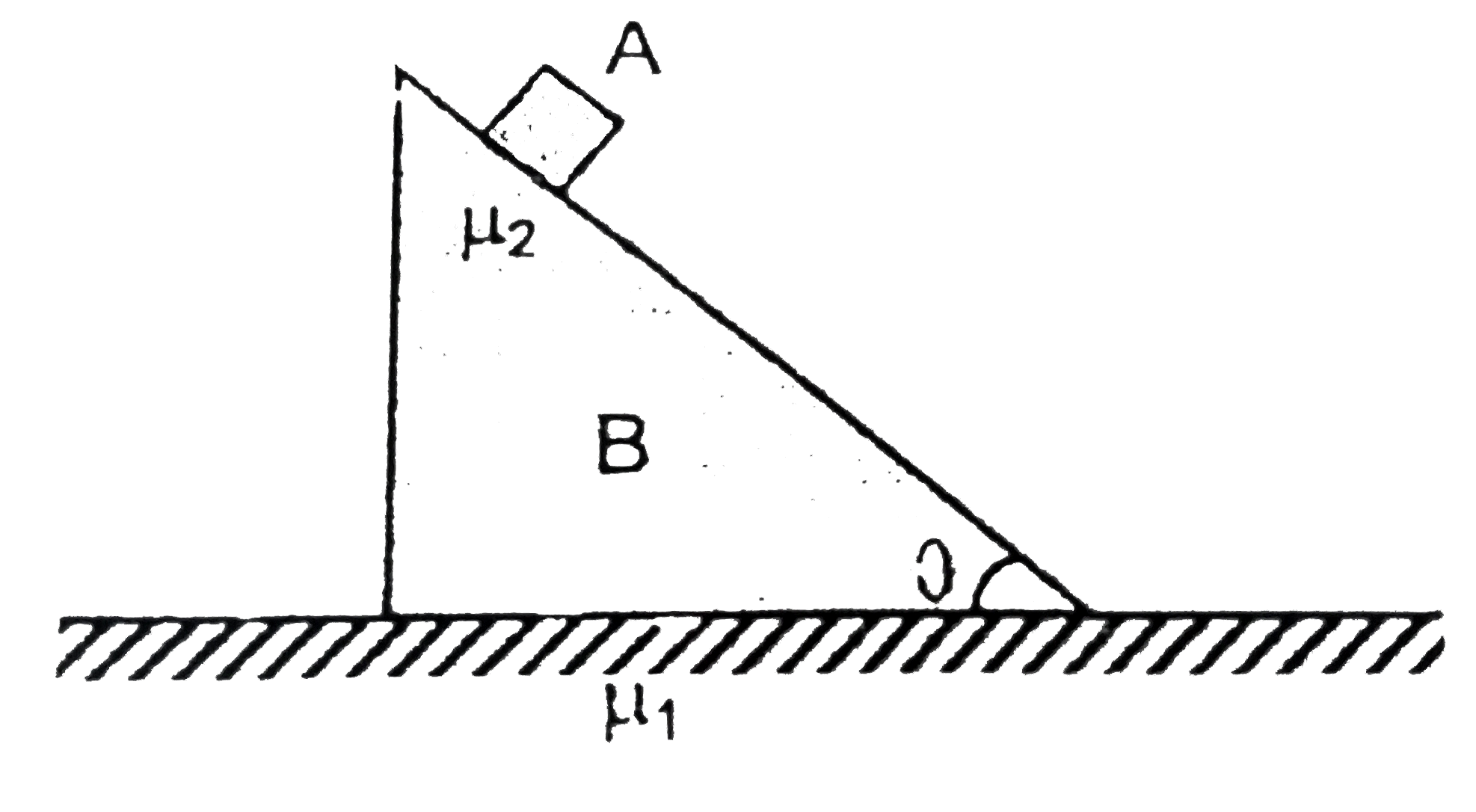
A wedge B of mass 2 m is placed on a rough horizontal suface. The coefficient of friction between wedge and the horizontal surface is μ1. A block of mass m is placed on wedge as shown in the figure. The coefficient of friction between block and wedge is μ2. The block and wedge are released from rest.
Q. Suppose the inclined surface of the wedge is at θ=37∘ from angle from horizontal and μ2=0 are wedge will remain in equilibrium if
View Solution

