In figure, an inextensible string that connects two bodies of mass M and m, passing over a fixed smooth pulley. The body M slides along a smooth vertical rigid bar. If the body M is released from the given position, find the maximum distance raised by body m.

Here we can use ΔK+ΔU=0.
Since initially, the system is at rest and finally it comes to rest (instaneously), the change of KE of the system is zero.
⇒ΔK=0
Also ΔU=0.
⇒(ΔU)M+(ΔU)m=0
Since the block m rises through a height h (say),
(ΔU)m=mgh
Similarly, the change in PE of the mass M is Mgh′, as it falls through a height h′, say
⇒mgh+(−Mgh′)=0⇒h′=mMh (i)
When the mass m ascends through a distance h, the length of the string between the pulley and the bar will be equal to (a+h).
Therefore, h′=√(a+h)2−a2⇒h′=√h(2a+h) (ii)
Eliminating h′ from (i) and (ii), we obtain
√h(2a+h)=mMh
⇒2a+h=m2M2h⇒h=2a(m2M2−1)
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.4
Explore 16 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.5
Explore 15 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.2
Explore 25 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
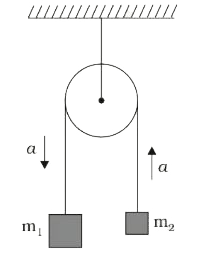
Two bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.
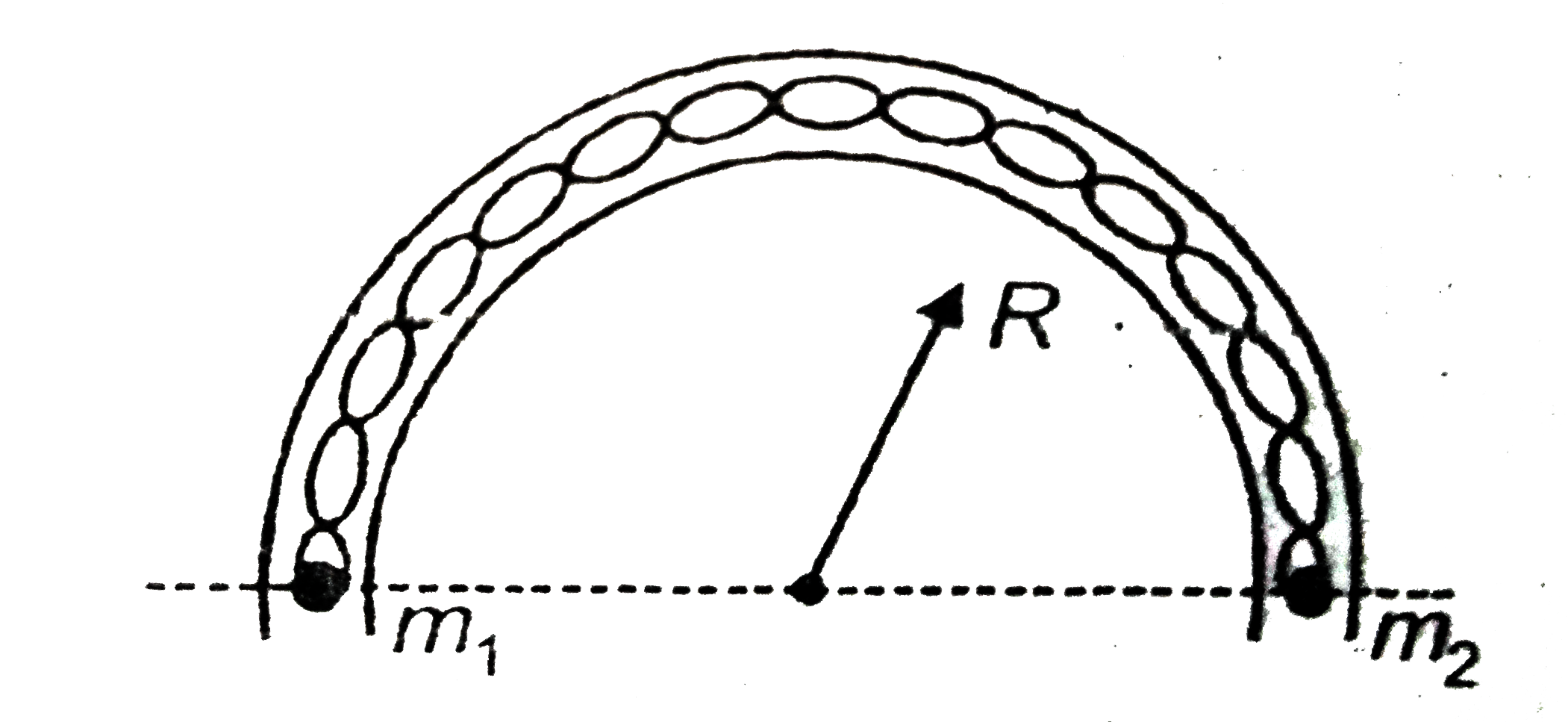
View SolutionTwo beads of masses m1andm2 connected by an inextensible string are kept at rest at the horizontal diametrical points of a fixed smooth vertical semicircular tube. If the beads are released from the given position, find their speeds as the function of vertical distance y converted by miss m2.
View Solution
Knowledge Check
Two bodies of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8m/s2)
A4.9m/s2B2.45m/s2C1.4m/s2D9.5m/s2Two bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
A(M−m)gBmgC2 mgD(m/M)mgTwo masses ,each equal to m ,are arrached to one another by a massless string passing over a smooth pulley the tension in the string is :
AmgB2mgCmg/2Dzero
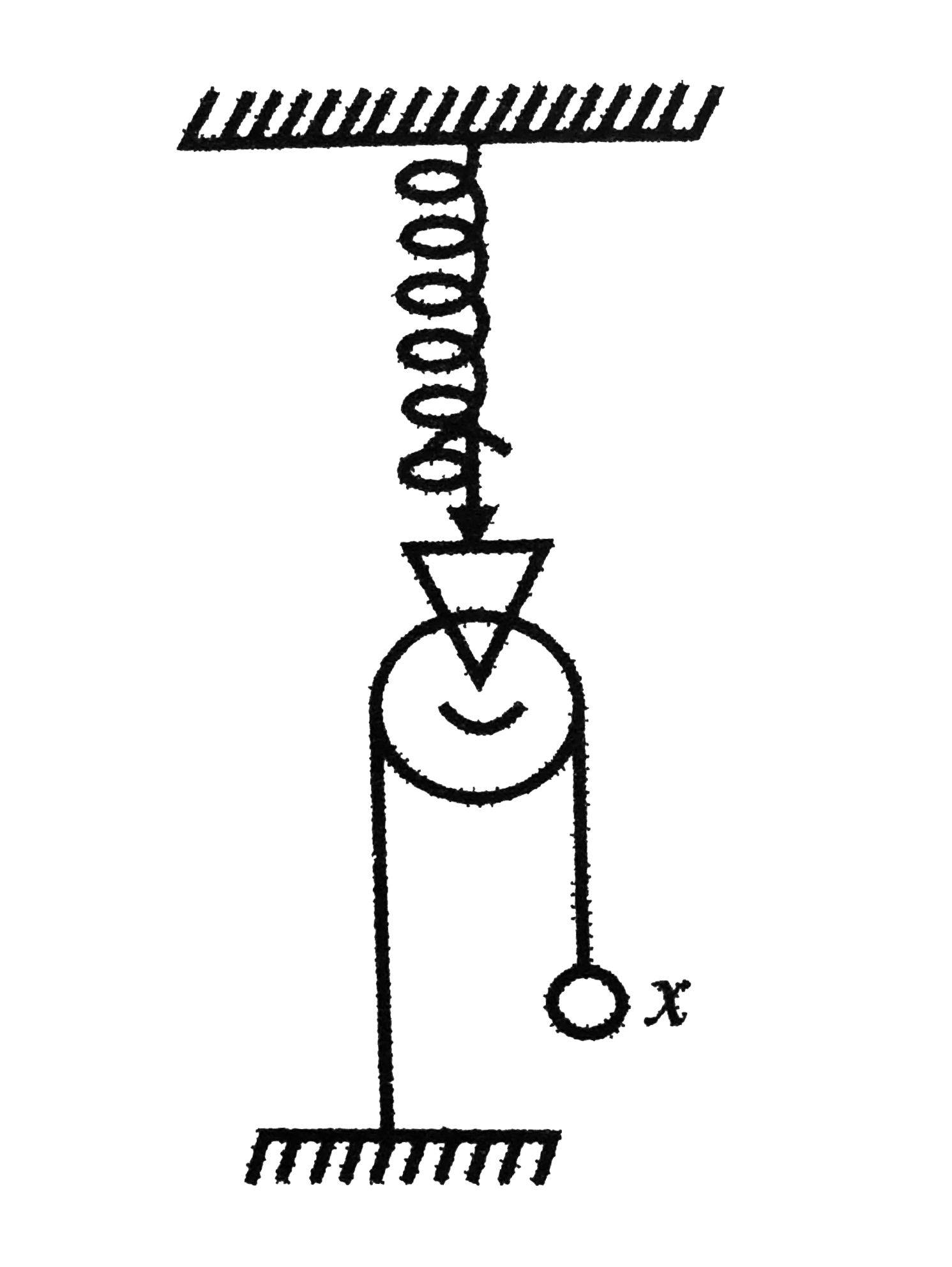
A body of mass m hangs by an inextensible string that passes over a smooth mass less pulley that is fitted with a light spring of stiffness k as shown in figure. If the body is released from rest and the spring is released, calculate the maximum elongation of the spring.
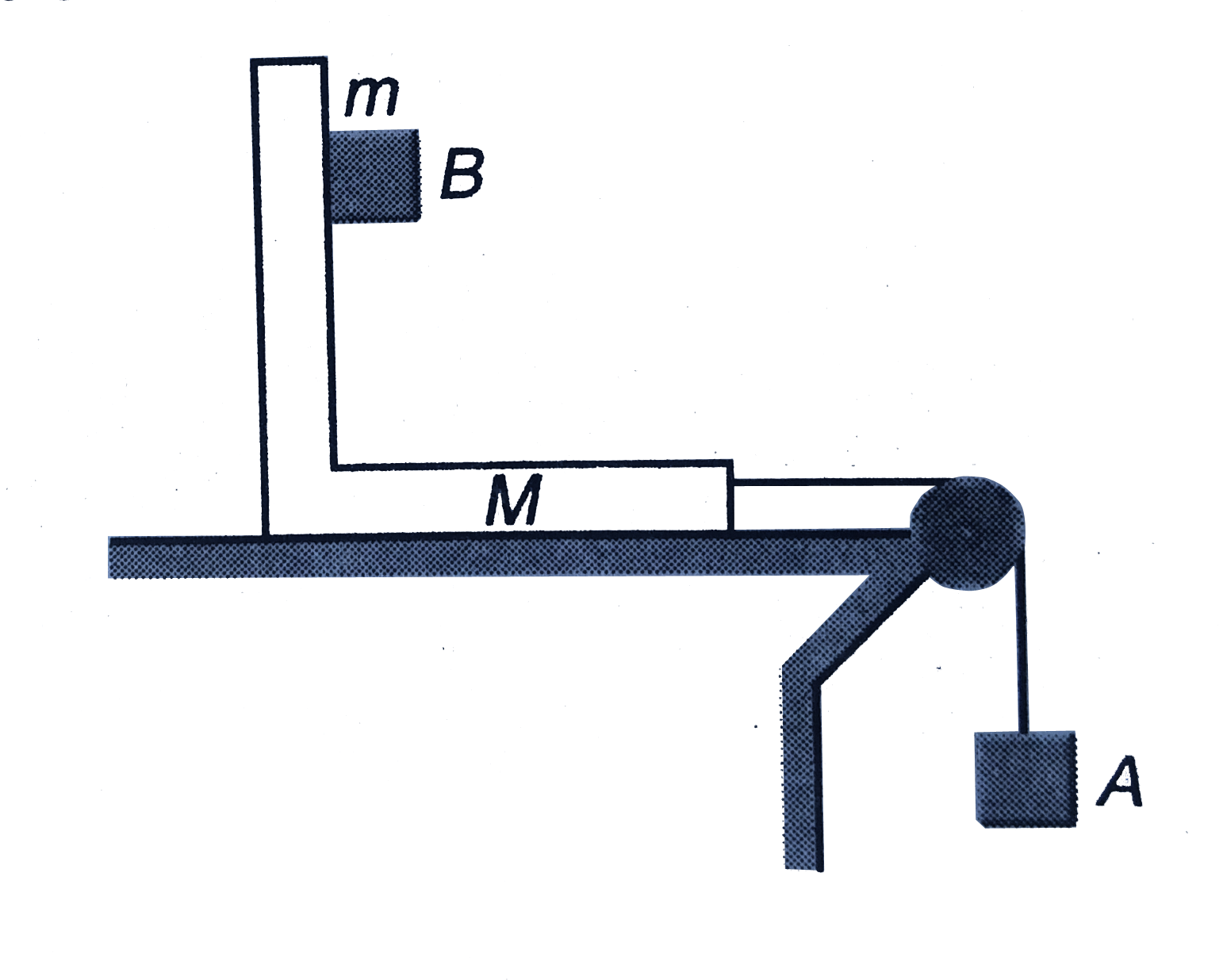
View SolutionThe figure an L shaped body of mass M placed on smooth horizontal surface. The block A is connected to the body by means of an inexiensible string , which is passing over a smooth pulley of negligible mass.Another block B of mass m is placed against a vertical wall of the body. Find the minimum value of the mass of block A so that B remain stationary relative to the wall. Coefficient of friction between the block B and the vertical wall is μ.
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
View SolutionTwo bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
View SolutionTwo bodies of masses m1 and m2 are separated by a distance R. The distance of the centre of mass of the bodies from the mass m1 is
View Solution