In the given system, when the ball of mass m is released, it will swing down the dotted arc.
a. How fast will it reach the lowest point in its swing? A nail is located at a distance d below the point of suspension.
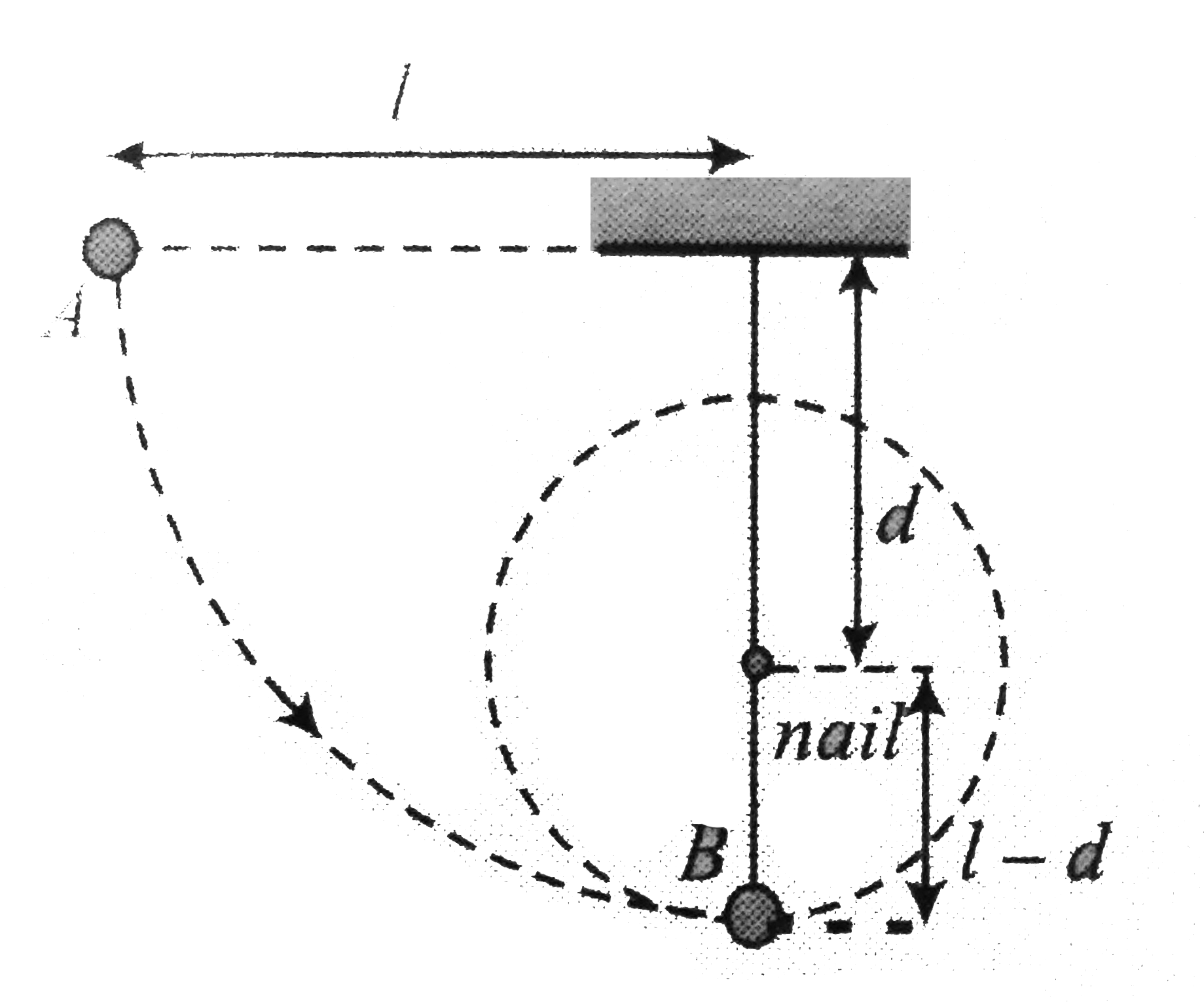
b. Show that d must at 0.6l, if the ball is to swing completely around a circle centered along the nail.
c. If d=0.6l, find the change in tension in the string just after it touches the nail.
a. Radius of the circle at nail =l−d. To complete the circle centered at nail, the speed at the bottom must be at least =√5g(l−d)
From A to B conserving mechanical energy ΔK+ΔU=0:
Loss in GPE=Gain in KE
mgl=12mv2⇒v=√2gl
b. To complete the circle: √2gl=√5g(l−d)
⇒5l−5d=2limpliesd=35l=0.6l
c. Just before touching the nail, the ball is moving in a circle of radius l.
⇒Tbefore−mg=mv2l
=mg+mv2l=mg+2mg=3mg

Just after touching the nail, the ball is moving in a circle of radius (l−d).
Tafter−mg=mv2(l−d)
=mg+mv2l−d=mg+m(2gl)0.4l
⇒Tension=6mg
Hence, the tension in the string changes from 3mg to 6mg as it touches the nail.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
In the given system, when the ball of mass m is released, it will swing down the dotted circular are. A nail is located at a distance d below the point of suspension as shown in figure.
(a) How fast will it reach the lowest point in its swing?
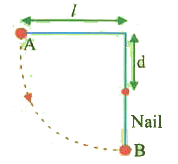
(b) Show that d must be at least 0.6l, if the ball is to swing completely around a circle centered along the nail.
(c) If d = 0.6 l, find the change in tension in the string just after it touches the nail.
View SolutionThe bob of a simple pendulum of length l is released from a point in the same horizontal line as the point of suspension and at a distance l from it Calculate the tension in the string at the lowest point of its swing
(b) If the string of the pendulum is catched by a nail located verticaly below the point of suspensions and the bob just swings around a complete circle around the nail, find the distance of the nail from the point of suspension
(c) If the string of the pendulum is made of rubber then show that it will be stretched by 3 mg/k on reaching the bob at the lowest point. Here k is the force constant of the string
View Solution
Knowledge Check
A pendulum comprising a light string of length L and small sphere, swings in the vertical plane . The string hits a peg located a distance of bellow the point of suspension (figure). If the pendulum is released from rest at the horizontal possition (θ=90∘) and is to swing in a complete circule centered on the peg, the minimum value of d is
 AL4B2L4C3L4D3L5
AL4B2L4C3L4D3L5A ball of mass m is fastened to a string. The ball swings in a vertical circle of radius R with the other end of the string held fixed. Neglecting the air resistance, the difference between the string's tension at the bottom of the circle and at the quarter of the cirlce is
AmgB3mgC4 mgD6 mgA pendulum of mass m and length l is released from rest in a horizontal position. A nail, a distance d below the pivot, causes the mass to move along the path indicated by the dotted line. The minimum distance such that the mass will swing completely round in the circle shown in figure is d then 5dL is
 A2B3C4D5
A2B3C4D5
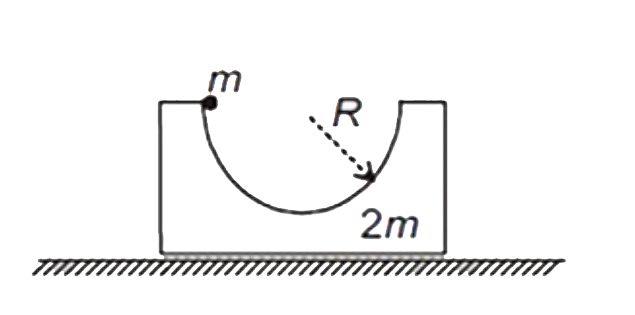
A small ball of mass m is released from rest from the position shown . All contact surface are smooth . The speed of the ball when it reaches its lowest position is
View SolutionA brass bob is suspended by an inextensible weightless string of length l from a peg fixed on a vertical wall. A nail is fixed in the wall at a distance d vertically below the point of suspension of the string. The bob is then drawn to a position where the string becomes horizontal and it is released from there. Show that d must be at least 0.6l if the bob is to swing completely around in a circle centred on the nail.
View SolutionA ball is attached to a horizontal cord of length l whose other end is fixed. (a) If the ball is released, what will be its speed at the lowest point of its path? (b) A peg is located a distance h directly below the point of attachment of the cord. If h=0.75l, what will be the speed of the ball when it reaches the top of its circular path about the peg?
View SolutionWhen will the motion of a simple pendulum be simple harmonic?
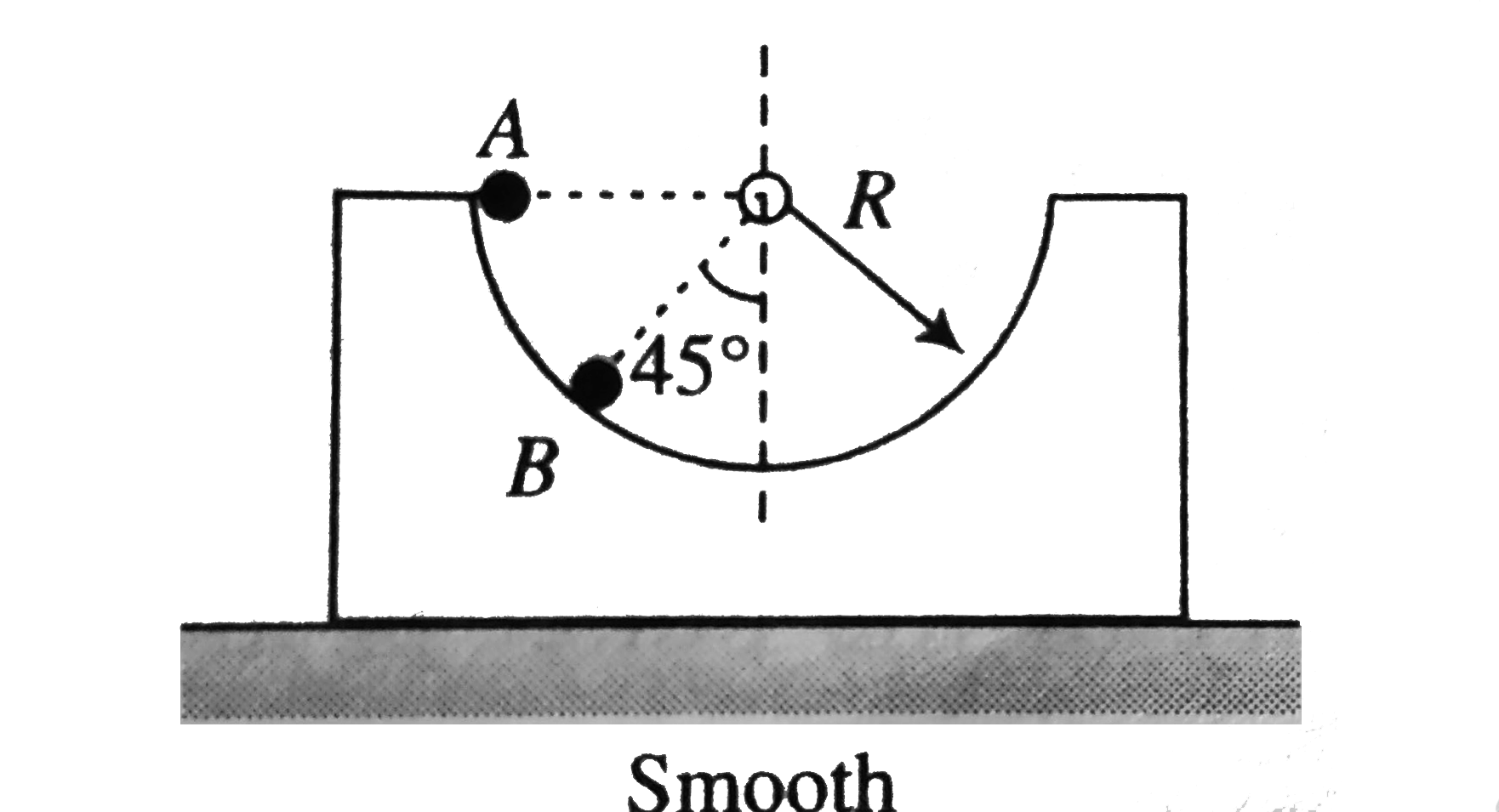
View SolutionA ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?
View Solution
