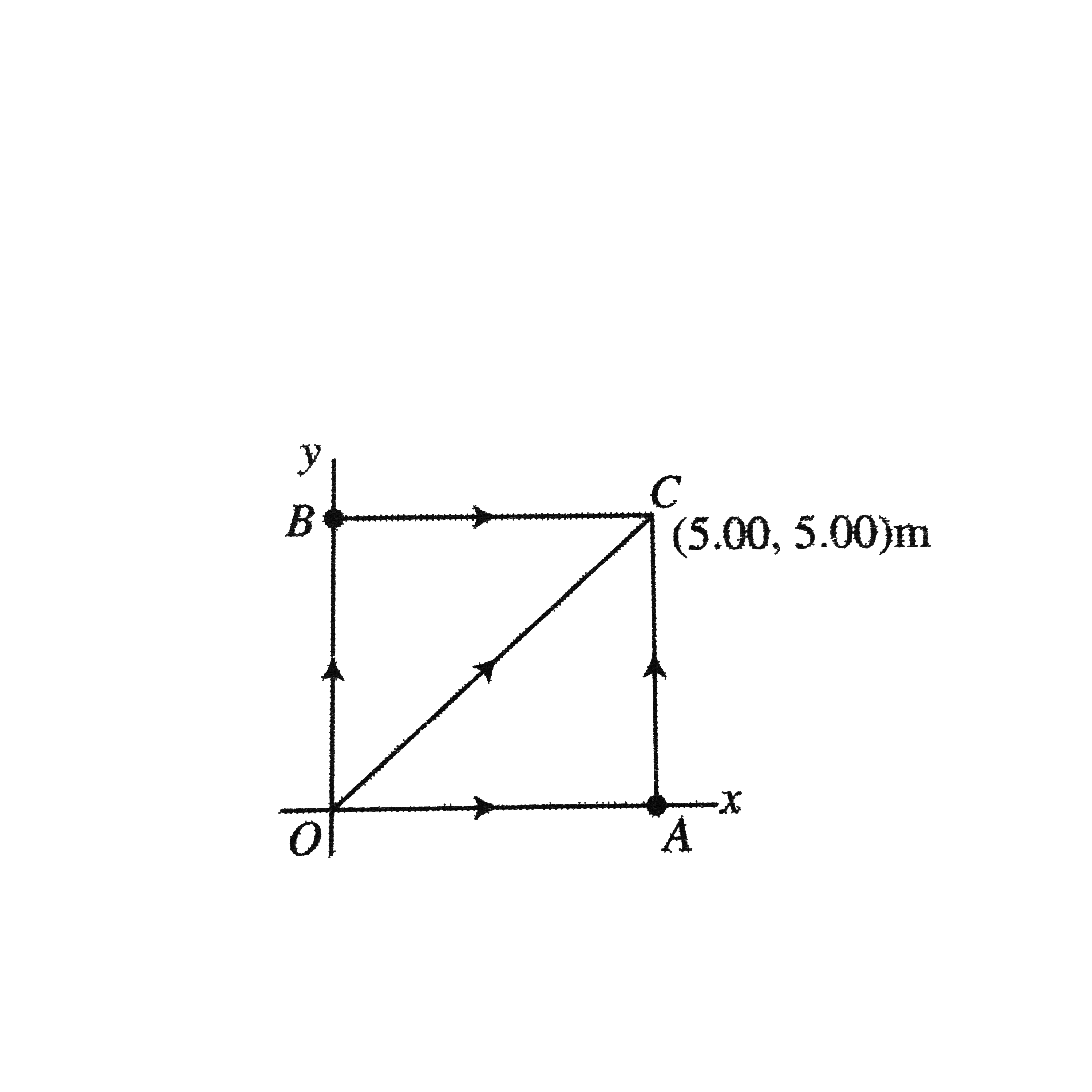
A 4.00−kg particle moves from the origin to position C, having coordinate x=5.00m and y=5m. One force on the particle is the gravitational force acting in the negative y direction. Using equation W=FΔrcosθ=→F.Δ→r, calculate the work done by the gravitional force on the particle as it goes from O to C along (a) OAC, (b) OBC, and (c) OC. Your results should all be identical. Why?
Fg=mg=(4.00kg)(10.0ms−2)=40.0N
a. Work done along OAC=Work along OA+Work along AC
=Fg(OA)cos90.0∘+Fg(AC)cos180∘
=(40.0N)(5.00m)cos90∘+(40.0N)(5.00m)cos180∘=−200J
b. Work done along OBC=W along OB+W along BC
=(40.0)(5.00m)cos180∘+(40.0N)(5.00m)cos90.0∘=−200J
c. Work done along OC=FgOCcos135∘
=(40.0N)(5.00×√2m)(−1√2)=−200J
Work done is same in all cases because gravitational force is a conservative force.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Force acting on a particle varies with x as shown in figure. Calculate the work done by the force as the particle moves from x = 0 to x = 6.0 m.
View SolutionCalculate the work done by the force →F=yˆi to move the particle from (0,0) to (1,1) in the following condition
(a) y = x (b) y = x2
View Solution
Knowledge Check
A particle moves along x -axis under the action of a position dependent force F =(5x2−2x)N. Work done by forces on the particle when it moves from origin to x=3m is
A45JB36JC32JD42JA particle moves along x - axis under the action of a position dependent force F=(5x2−2x)N. Work done by force on the particle when it moves from origin to x = 3 m is
A45 JB36 JC32 JD42 JA force of F=(0.5x+12)N acts on a particle. If x is in metre, calculate the work done by the force during the displacement of the particle from x = 0 to x = 4 m
A128 JB80 JC64 JD52 J
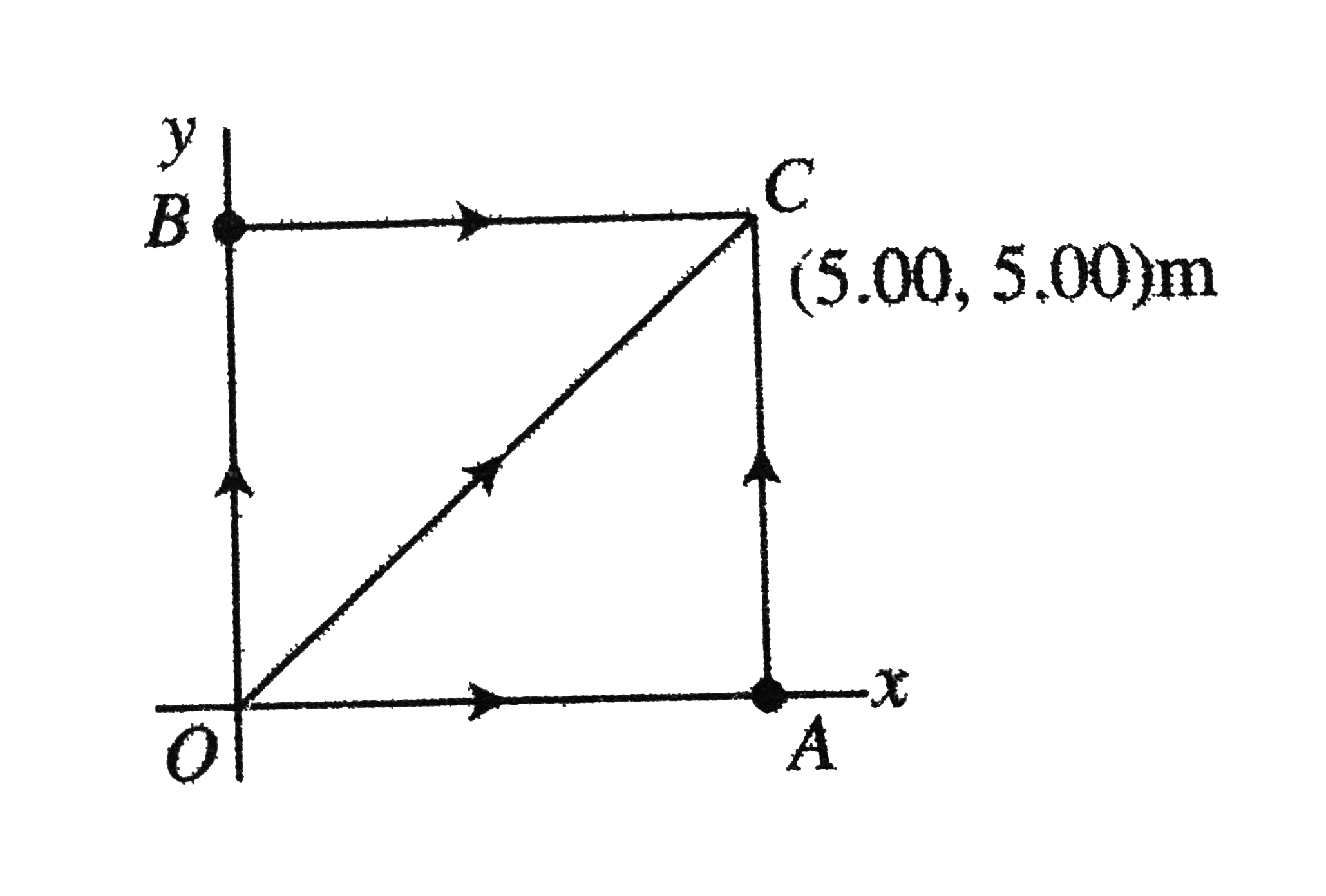
A force acting on a particle moving in the x-y plane is given by →F=(2yˆi+x2ˆj)N, where x and y are in meters. The particle moves from the origin to a final position having coordinates x=5.00m as shown in figure. Calculate the work done by →F on the particle as it moves along (a) OAC, (b) OBC, and (c) OC. (d) Is →F conservative or non-conservative? Explain.
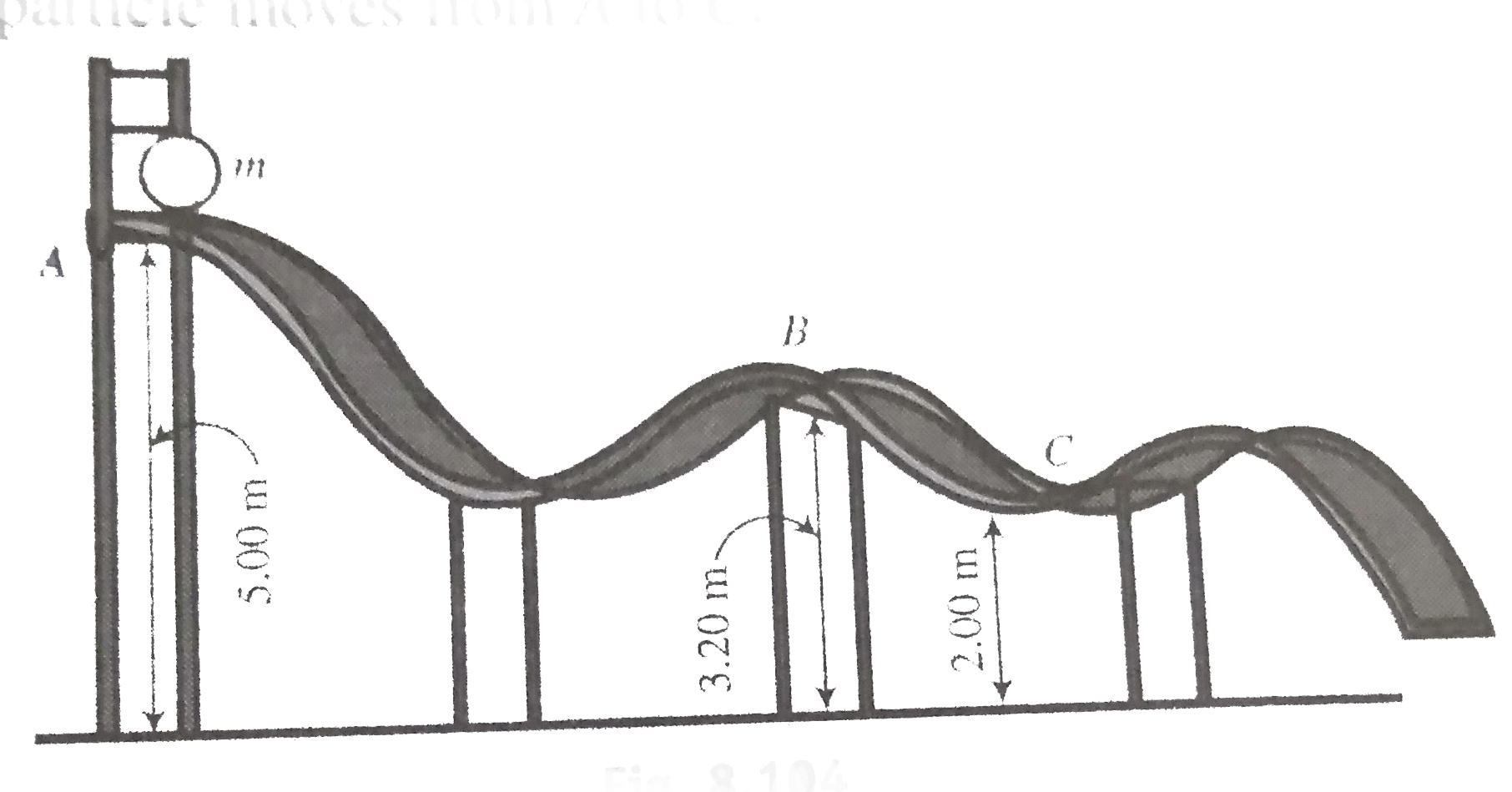
View SolutionA particle of mass m=5.00kg is released from point A and it slides on the frictionless track shown in figure. Determine (a) the particle's speed at points B and C and (b) the net work done by the gravitational force as the particle moves from A to C.
View SolutionA force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.
View SolutionA block of mass 5kg initially at rest at the origin is acted upon by a force along the positive X−direction represented by
F=(20+5x)N. Calculate the work done by the force during the displacement of the block from x=0 to x=4m.
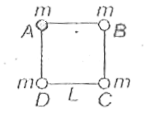
View SolutionFour particles A,B, C and D each of mass m are kept at the corners of a square of side L. Now the particle D is taken to infinity by an external agent keeping the other particles fixed at their respective positions . The work done by the gravitational force acting on the particle D During its movement is
View Solution
