Calculate the work done by the force vec(F) = y hat(i) to move the par

The work done by a force $\to F = (- 6 x^{3} ˆ i)$ N in displacing a particle from x = 4m to x = - 2m is
A $- 240 J$
B $360 J$
C $420 J$
Dwill depend upon the path
The work done by the force $\to F = A (y^{2} ˆ i + 2 x^{2} ˆ j)$ , where A is a constant and x & y are in meters around the path shown is :

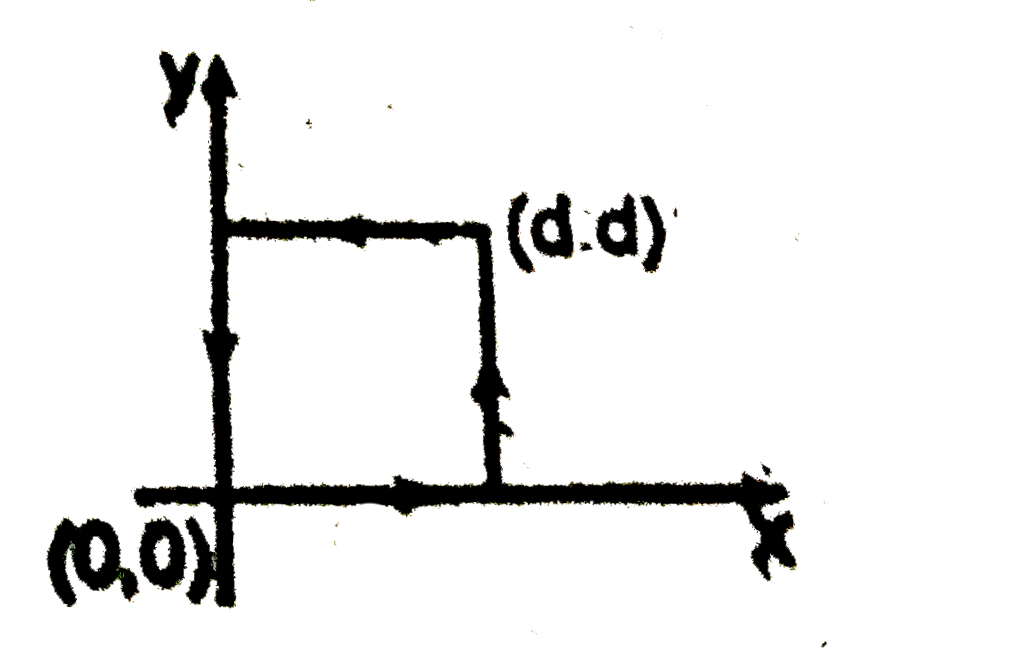Azero
BAd
C $A d^{2}$
D $A d^{3}$
Consider a force $r F = - x^{3} ˆ i + y^{2} ˆ j$ .The work done by this force in moving a particle from A(1,0) to B(0,1) along a straight line is $:$ ( All quantities are in SI units )
A1
B $\frac{5}{12}$
C $\frac{7}{12}$
D $\frac{3}{4}$

Calculate the work done by the force $\to F = y ˆ i$ to move the particle from (0,0) to (1,1) in the following condition
(a) y = x (b) y = $x^{2}$