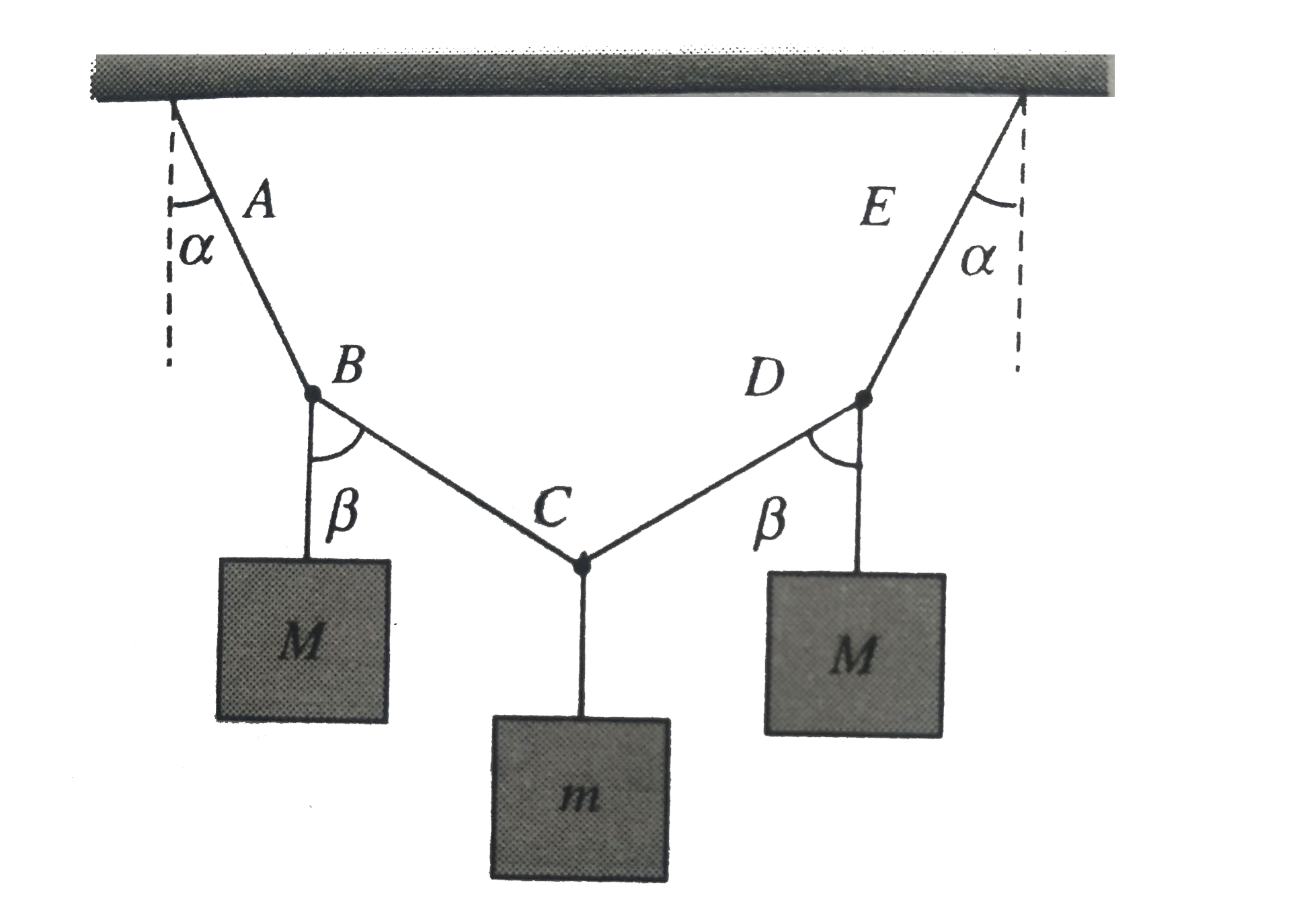
Figure, represents a light inextensible string ABCDE in which AB=BC=CD=DE and to which are attached masses M,m, and M at the point B,C and D, respectively. The system hangs freely in equilibrium with ends A and E of the string fixed in the same horizontal line. it is given that tanα=3/4 and tanβ=12/5. Then the tension in the string BC is
2mg
(13/10)mg
(3/10)mg
(20/11)mg
The correct Answer is:B
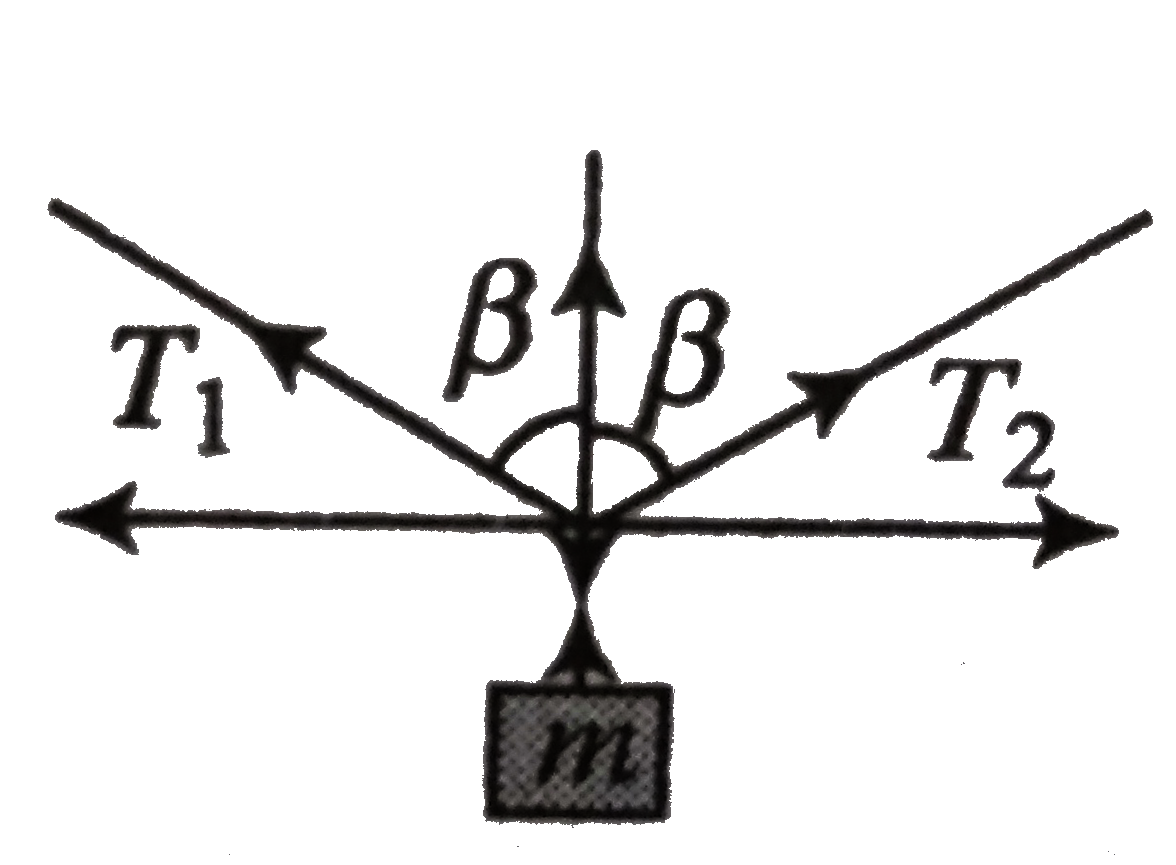
tanβ=125∴cosβ=513
T1cosβ+T2cosβ=mg …(i)
T1sinβ=T2sinβ …(ii)
∴T1=T2=T
∴2Tcosβ=mg⇒T=mg2cosβ⇒T=1310mg.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
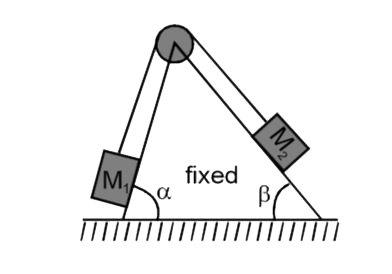
Two masses M1 and M2 are attached to the ends of a light string which passes over a massless pulley attached to the top of a double inclined smooth plane of angles of inclination α and β.The tension in the string is :
View SolutionA ball of mass m is attached to a fixed point by a light inextensible string describe a circle in a verticle plane. The tension in the string has the values αmg and βmg, respectively, when the particle is at the highest and the lowest point in the path. find the relation between α and β.
View Solution
Knowledge Check
- Question 1 - Select One or More
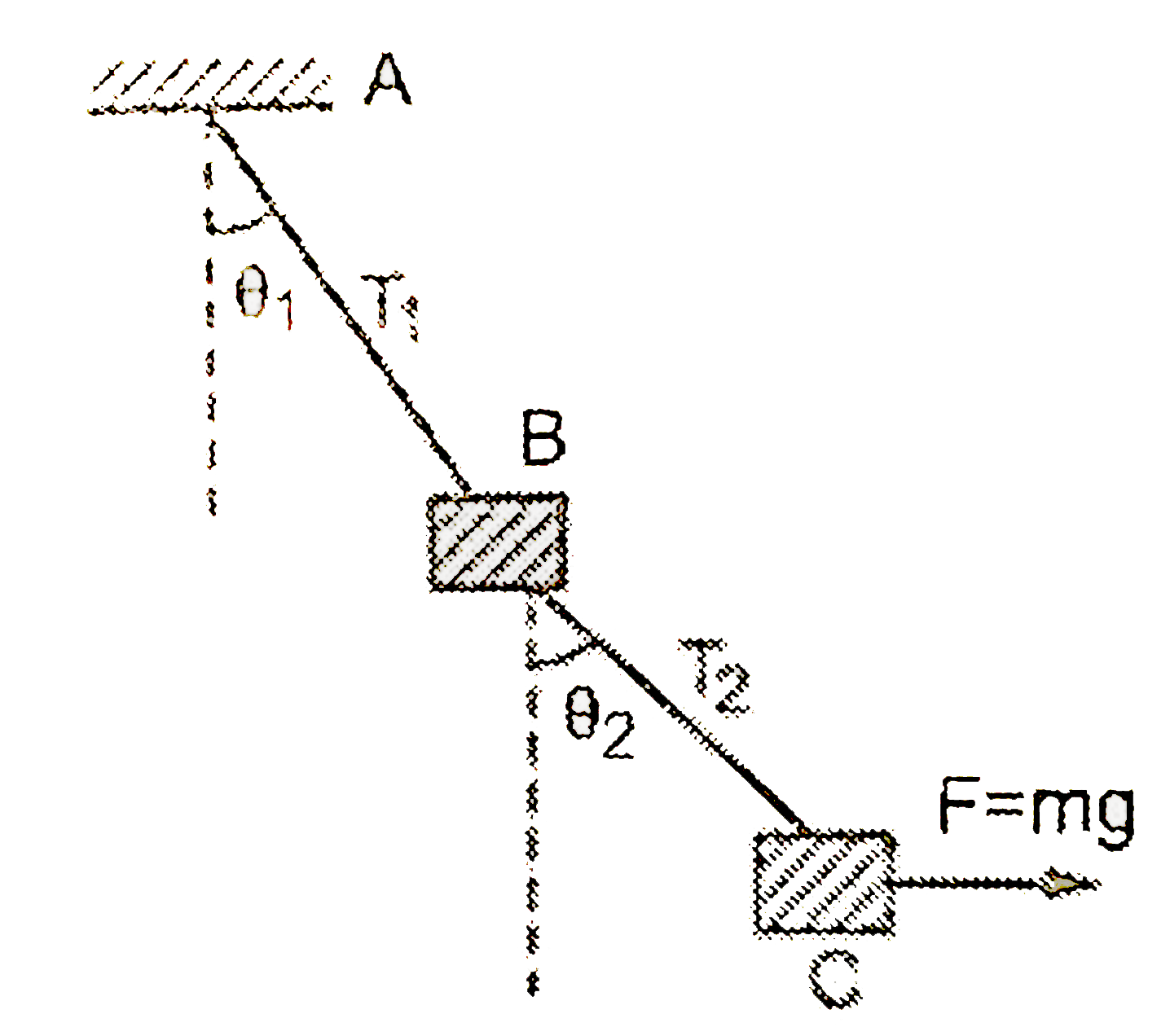
The blocks B and C in the figure have mass m each. The strings AB and BC are light, having tensions T1 and T2 respectively. The system is in equilibrium with a constant horizontal force mg acting on C.Atanθ1=1/2Btanθ2=1CT1=√5mgDT2=√2mg - Question 2 - Select One
The blocks B and C in the figure have mass m each. The strings AB and BC are light having tension T1 and T2 respectively. The system is in equilibrium with a constant horizontal forcemg acting on C. Then which one is incorrect.
Atanθ1=12Btanθ=1CT1=√5mgDT2=mg - Question 3 - Select One
A body of mass m hangs at one end of a string of length l , the other end of which is fixed. It is given a horizontal velocity so that the string would just reach where it makes an angle of 60∘ with the vertical. The tension in the string at mean position is
A2mgBmgC3mgD√3mg
A block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.View SolutionAn L shaped uniform rod of mass 2M and length 2L(AB=BC=L) is held as shown in Fig. with a string fixed between C and wall so that AB is vertical and BC is horizontal. There is no friction between the hinge and the rod at A.
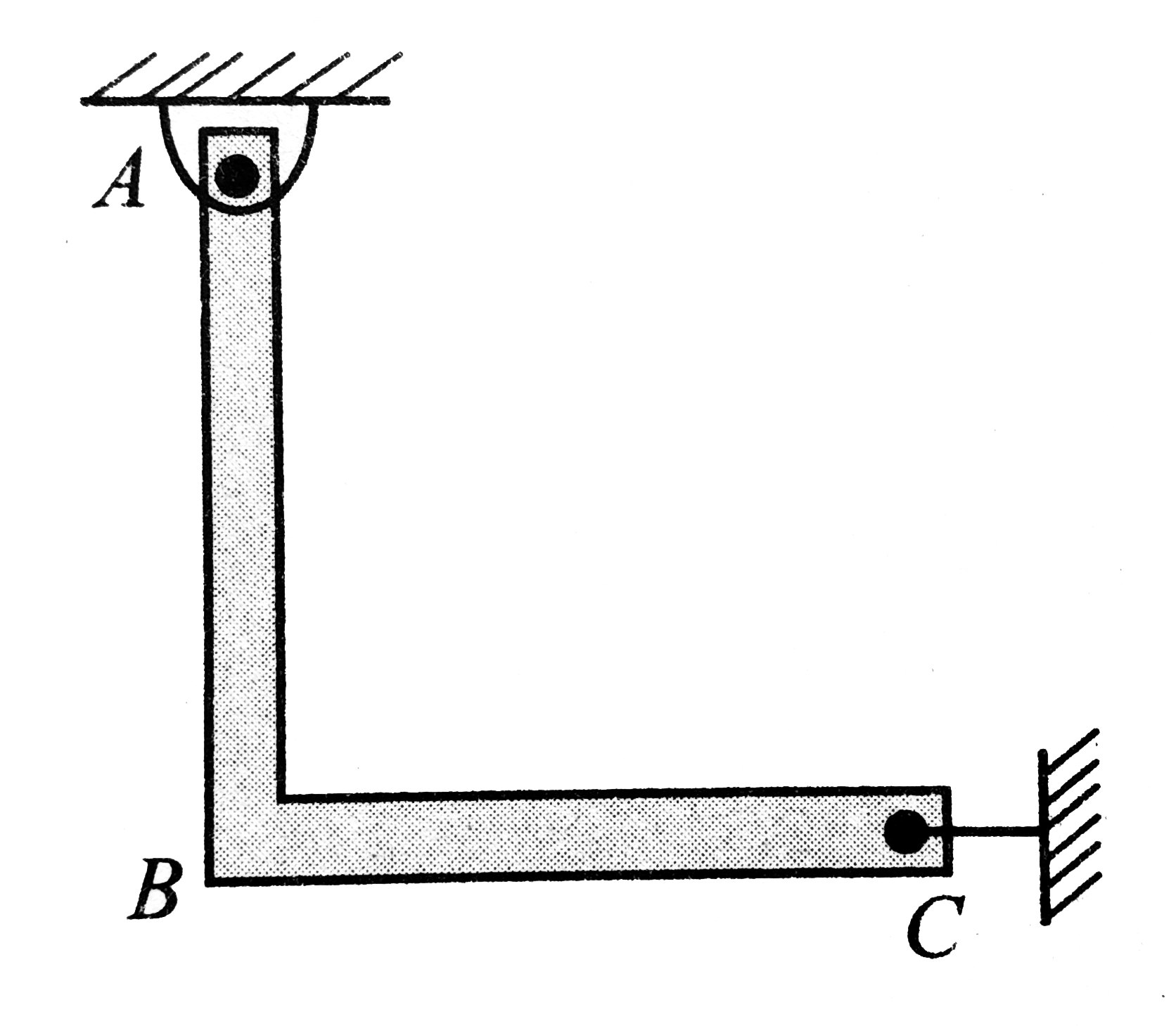
Find the tension in the stringView SolutionA body of mass m hangs at one end of a string of length l, the other and of which is fixed . It is given a horizontal velocity so that the string would just reach where it makes an angle of 30∘ with the vertical . The tension in the string at mean position is
View SolutionA mass M is suspended by a rope from a rigid support at A as shown in figure. Another rupe is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
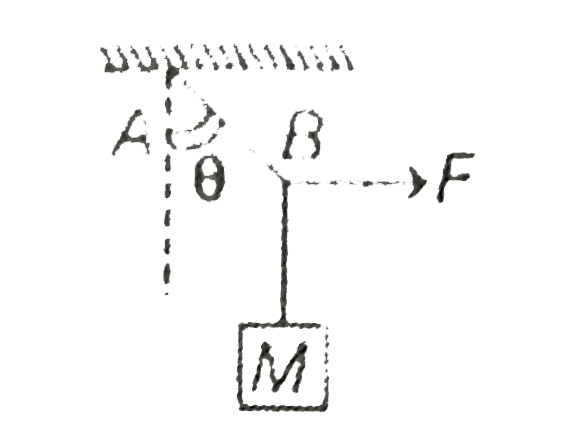
View Solution