A block is lying on the horizontal frictionless surface. One end of a uniform rope is fixed to the block which is pulled in the horizontal direction by applying a force F at the other end. If the mass of the rope is half the mass of the block. The tension in the middle of the rope will be
F
2F/3
3F/5
5F/6
The correct Answer is:D
The acceleration of block-rope system is a=F(M+m)
where M is the mass of block and m is the mass of rope.
So the tension in the middle of the rope will be
T={M+(m/2)}a=M+(m/2)FM+m
Given that m=M/2
∴T=[M+(M/4)M+(M/2)]=F=5F6.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Multiple Correct
Explore 11 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Assertion-reasoning
Explore 15 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Subjective
Explore 15 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point

View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force P is applied at the free end of the rope, the force exerted by the rope on the block will be
View Solution
Knowledge Check
A block of mass m is resting one a smooth horizontal surface. One end of a uniform rope of mass m/3 is fixed to the block, which is pulled in the horizontal direction by applying force F at the other end. The tension in the middle of the rope is
A86FB17FC18FD78FA block of mass m is resting one a smooth horizontal surface. One end of a uniform rope of mass m/3 is fixed to the block, which is pulled in the horizontal direction by applying force F at the other end. The tension in the middle of the rope is
A87SB17FC18FD78FA block of mass M is resting on a smooth horizontal plane. One end of a uniform rope of mass M4 is fixed to the block , which pulled it in the horizontal direction by applying a force F at the other ends . The tension in the middle of the rope is
AF2BF5C910FDF
A block of mass M is attached to a uniform rope of mass m. This arrangement is pulled by applying a force F at the rope as shown. Find the tension in the rope (a) at the junction of the rope and the block (b) at the mid point of the rope.
View SolutionA block rests on a horizontal surface. A horizontal force F is applied to the block. The acceleration (a) produced in the block as a function of applied force (F) has been plotted in a graph (see figure). Find the mass of the block.
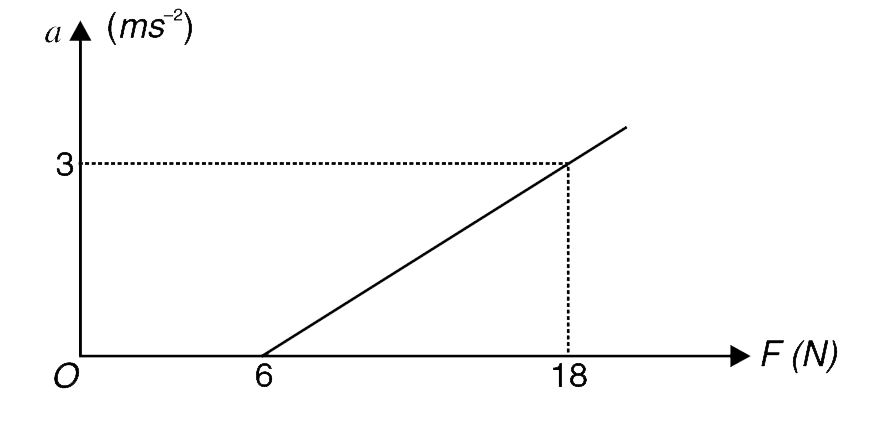
View SolutionThe block is placed on a frictionless surface in gravity free space. A heavy string of a mass m is connected and force F is applied on the string, then the tension at the middle of rope is

View SolutionA block of mass m is pulled by a uniform chain of mass m tied to it by applying a force F at the other end of the chain. The tension at a point P which is at a distance of quarter of the length of the chain from the free end, will be
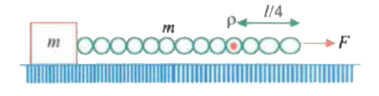
View SolutionA block of mass m is pulled by a uniform chain of mass m tied to it by applying a force F at the other end of the chain.The tension at a point P which is at a distance of quarter of the length of the chain from the free end,will be

View Solution

