A U-shaped smooth wire has a semi-circular bending between A and B as shown in fig. A bead of mass m moving with uniform speed v through the wire enters the semiculcular bent at A and leaves at B. Find the average force exerted by the bead on the part AB of the wire.

0
4mv2πd
2mv2πd
None of these
The correct Answer is:B
Choosing the position x-y axis as shown in the figure, the momentum of the bead at A is →Pi=+m→v.
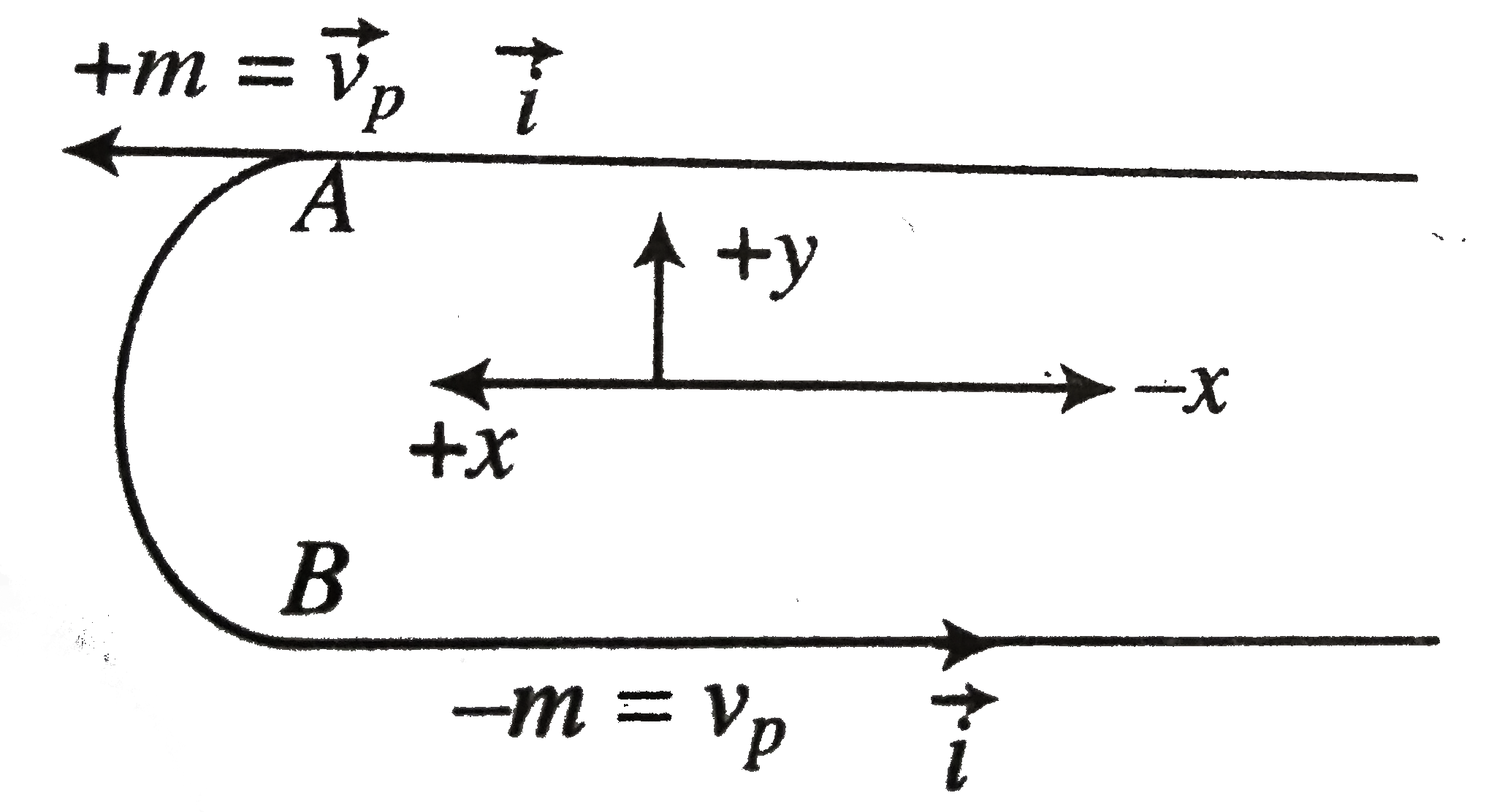 The momentum of the bead at B is →Pf=−m→v.
The momentum of the bead at B is →Pf=−m→v.
Therefore, the magnitude of the change in momentum between A and B is Δ→P=→Pf−→Pi=−2m→v,i.e.,Δ(p)=2mv along the positive x axis.
The time taken by the bead to reach from A and B is
Δt=π.d/2v=πd2v
Therefore, the average force exerted by the bead on the wire is
Fav=ΔpΔp=(2mv/πd2v)=4mv2πd.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Multiple Correct
Explore 11 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Assertion-reasoning
Explore 15 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Subjective
Explore 15 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
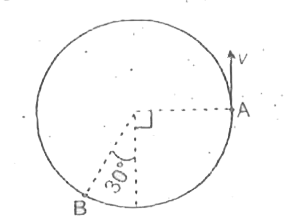
A particle of mass m moves with constant speed v on a circular path of radius r as shown in figure. The average force on it during its motion from A to B is
View SolutionA copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular ot the diameter joining free ends, (b) the velocity is parallel to this diameter.
View Solution
Knowledge Check
A fixed U-shaped smooth wire has a semi-circular bending between A and B as shown in the figure. A bead of mass 'm' moving with uniform speed v through the wire enters the semicircular bend at A and leaves at B. The magnitude of average force exerted by the bead on the part AB of the wire is
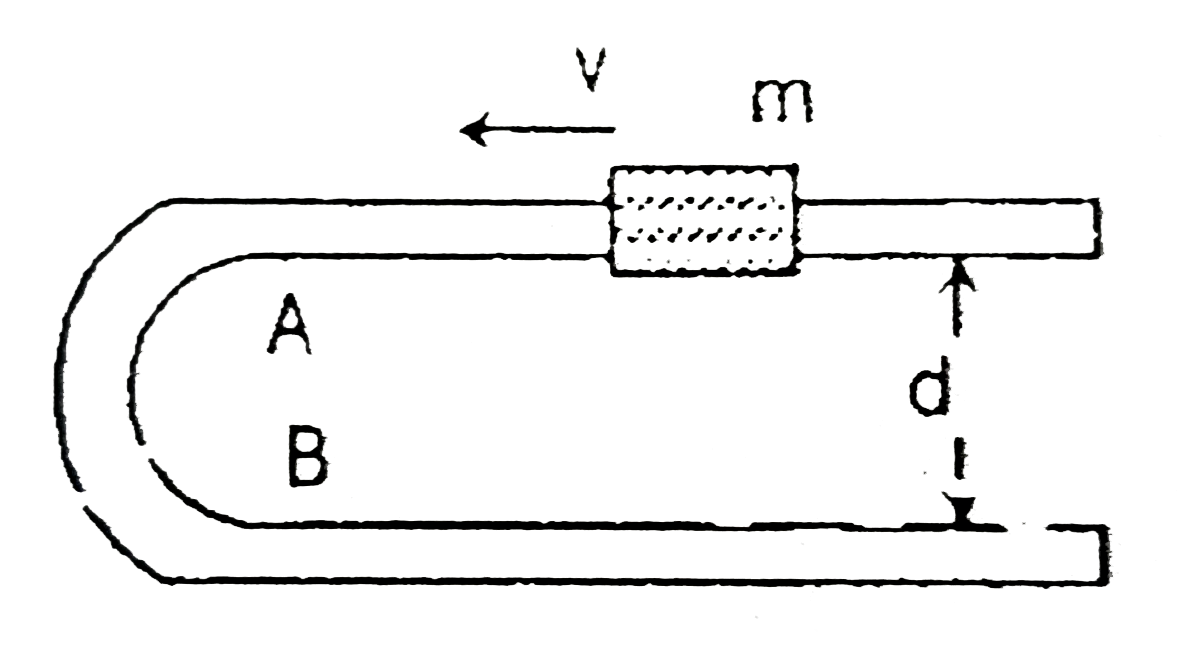 A0B4mv2πdC2mv2πdDNone of these
A0B4mv2πdC2mv2πdDNone of theseA U-shaped wire has a semicircular bending between A and B as shown in Fig. A bead of mass m moving with uniform speed v through a wire enters the semicircular bend at A and leaves at B with velocity v/2 after time T. The average force exerted by the bead on the part AB of the wire is
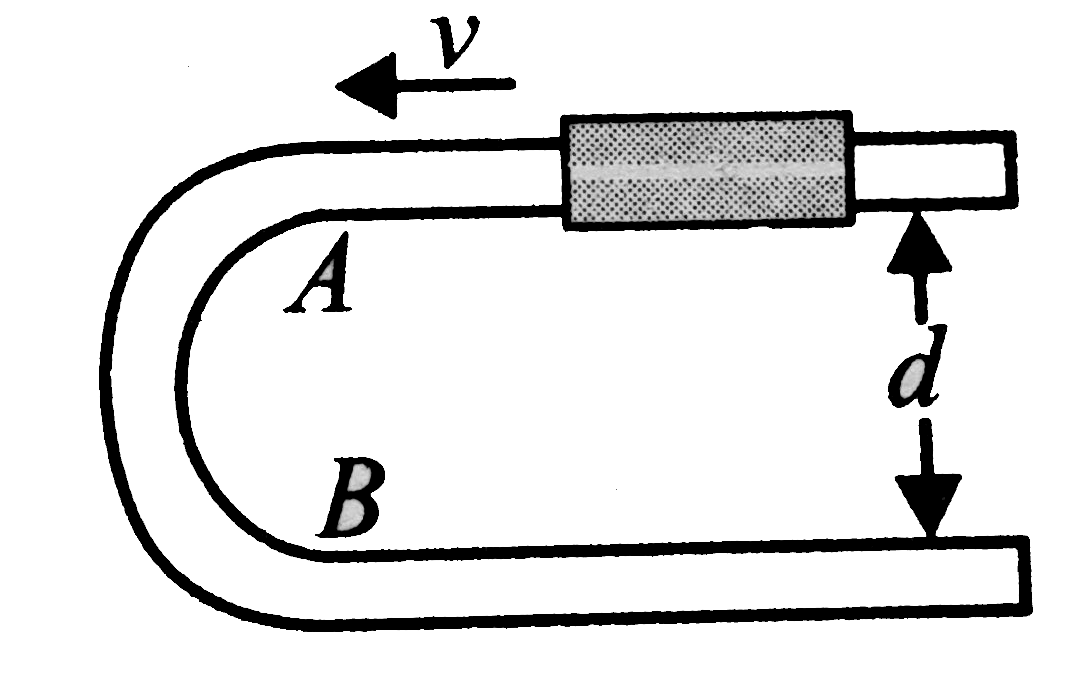 A0B3mv2TC3mvTDnone of these
A0B3mv2TC3mvTDnone of theseConsider a U- shaped fixed smooth wire over which a bead of mass (m) is thrown with speed v.

The bead enters semicircular part at A and leaves at B. What is the magnitude of average force exerted by the bead on the part AB of the wire ?Amv2πdB2mv2πdC4mv2πdD0
In a trapeze-shaped structure, two rigid wires of negligble mass support a conducting bar of mass m and length L as shown in Fig. A source of emf is applied to the wires so that a current I flows through the bar. A uniform magnetic field →B is perpendicular to the plane of the wires and bar.
a. Compute the current that the source of emf must provide so that there is no tension in the wires.
b. If the current is reduced to half the value computed in (a) and the plane of the structure is moved through an angle θ, compute the tension in the wires and the magnitude of the net unbalanced force on the bar at the instant it is released from this angle.

View SolutionA small, electrically charged bead can slide on a circular, frictionless, thin, insulating ring. Charge on the bead is Q and its mass is m . A small electric dipole, having dipole moment P is fixed at the centre of the circle with the dipole’s axis lying in the plane of the circle. Initially, the bead is held on the perpendicular bisector of the dipole (see fig.) Ignore gravity and answer the following questions.
(a) Write the speed of the bead when it reaches the position θ shown in the figure. (b) Find the normal force exerted by the ring on the bead at position θ. (c) How does the bead move after it is released? Where will the bead first stop after being released? (d) How would the bead move in the absence of the ring?

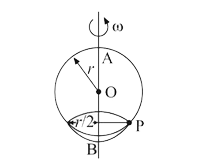
View SolutionA smooth wire of length 2πr is bent into a circle and kept in a vertical plane. A bead can slide smoothly on the wire. When the circle is rotating with angular speed about the vertical diameter AB, as shown in the figure, the bead is at rest with respect to the circular ring at potion P as shown. Then the value of ω2 is equal to:
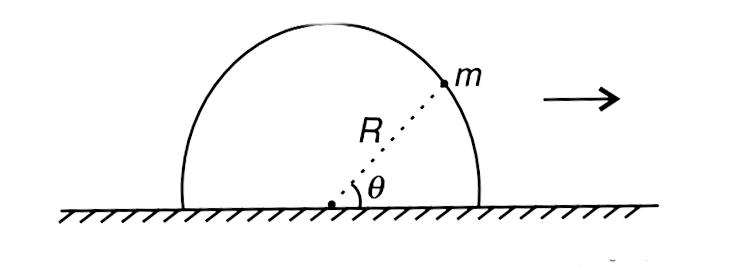
View SolutionA semicircular wire frame of radius R is standing vertical on a horizontal table. It is pulled horizontally towards right with a constant acceleration. A bead of mass m remain in equilibrium (relative to the semicircular wire) at a position where radius makes an angle q with horizontal. There is no friction between the wire and the bead. The bead is displaced a little bit in upward direction and released. Calculate the speed of the bead relative to the wire at the instant it strikes the table. Assume that all throughout the semicircular wire keeps moving with constant acceleration.
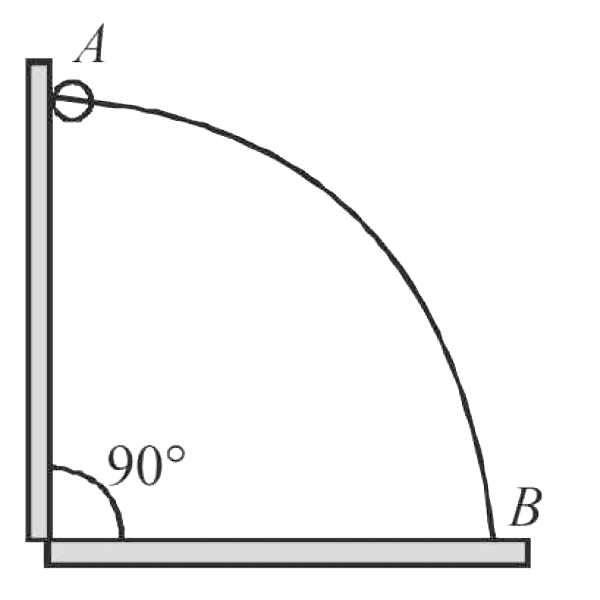
View SolutionA wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
View Solution

