A heavy particle is projected with a velocity at an angle with the horizontal into the uniform gravitational field. The slope of the trajectory of the particle varies as
A
 .
.
B
 .
.
C
 .
.
D
 .
.
Video Solution
Text Solution
The correct Answer is:B, C, D
(b.,c.,d.) If the particle is projected with velocity u at an angle θ, then equation of its trajectory will be
y=xtanθ−gx22u2cos2θ
We know slope is given by m=dydx
Therefore, slope m=tanθ−gxu2cos2θ
It implies that the graph between slope and x will be straight line having negative slope and a non - zero positive intercept on y - axis.
But x is directly proportional to the time t, therefore, the shape of graph between slope and time will be same as that of the graph between slope and x. Hence, only option (a) is correct, i.e., options (b),(c)and (d) are incorrect.
|
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Assertion - Reasoning
Explore 5 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Comprehension
Explore 21 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Single Correct
Explore 76 Videos
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
Knowledge Check
A heavy particle is projected with a velocity at an acure angle with the horizontal into a uniform gravitational field. The slope of the trajectory of the particle varies as
A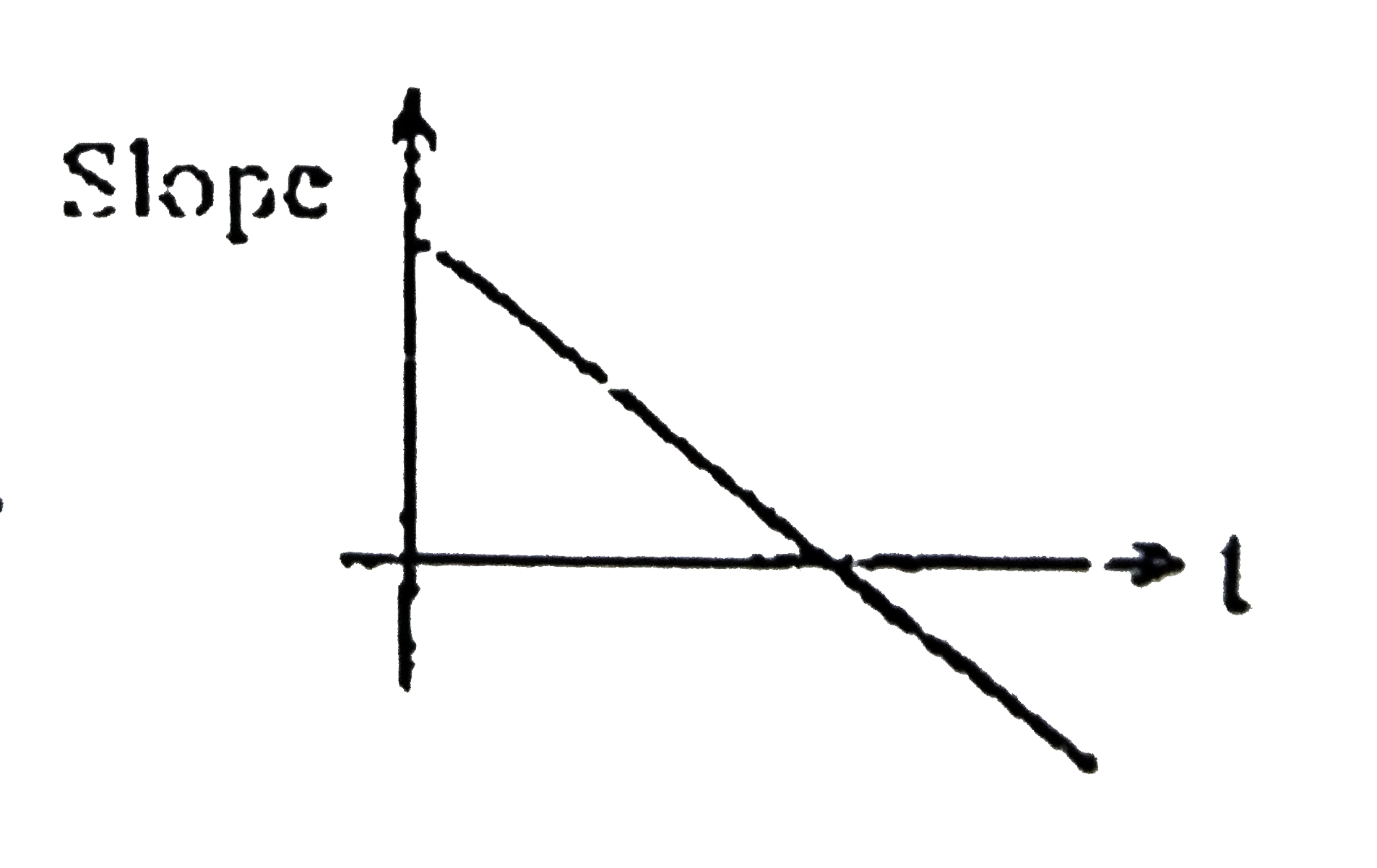 B
B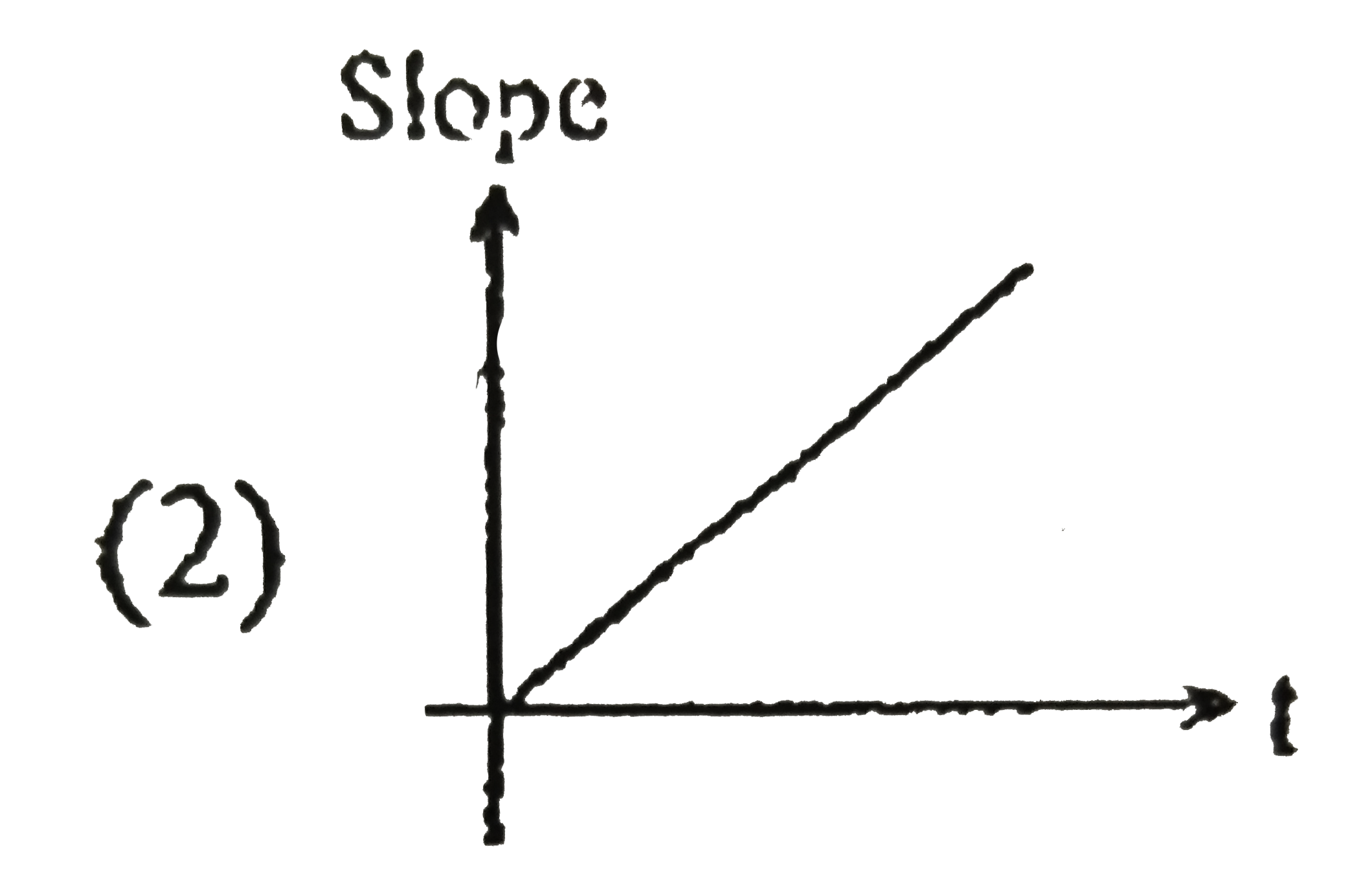 C
C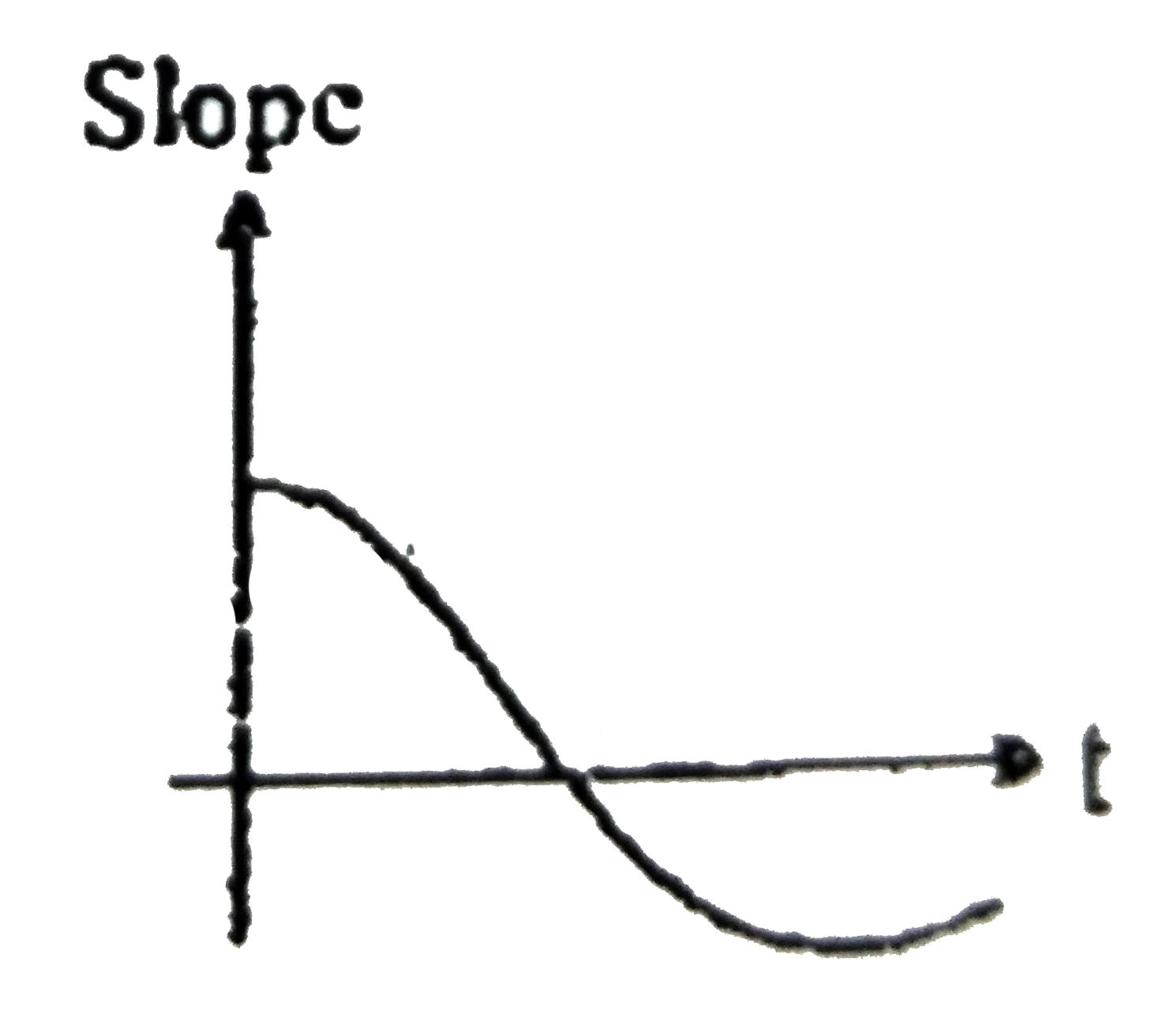 D
D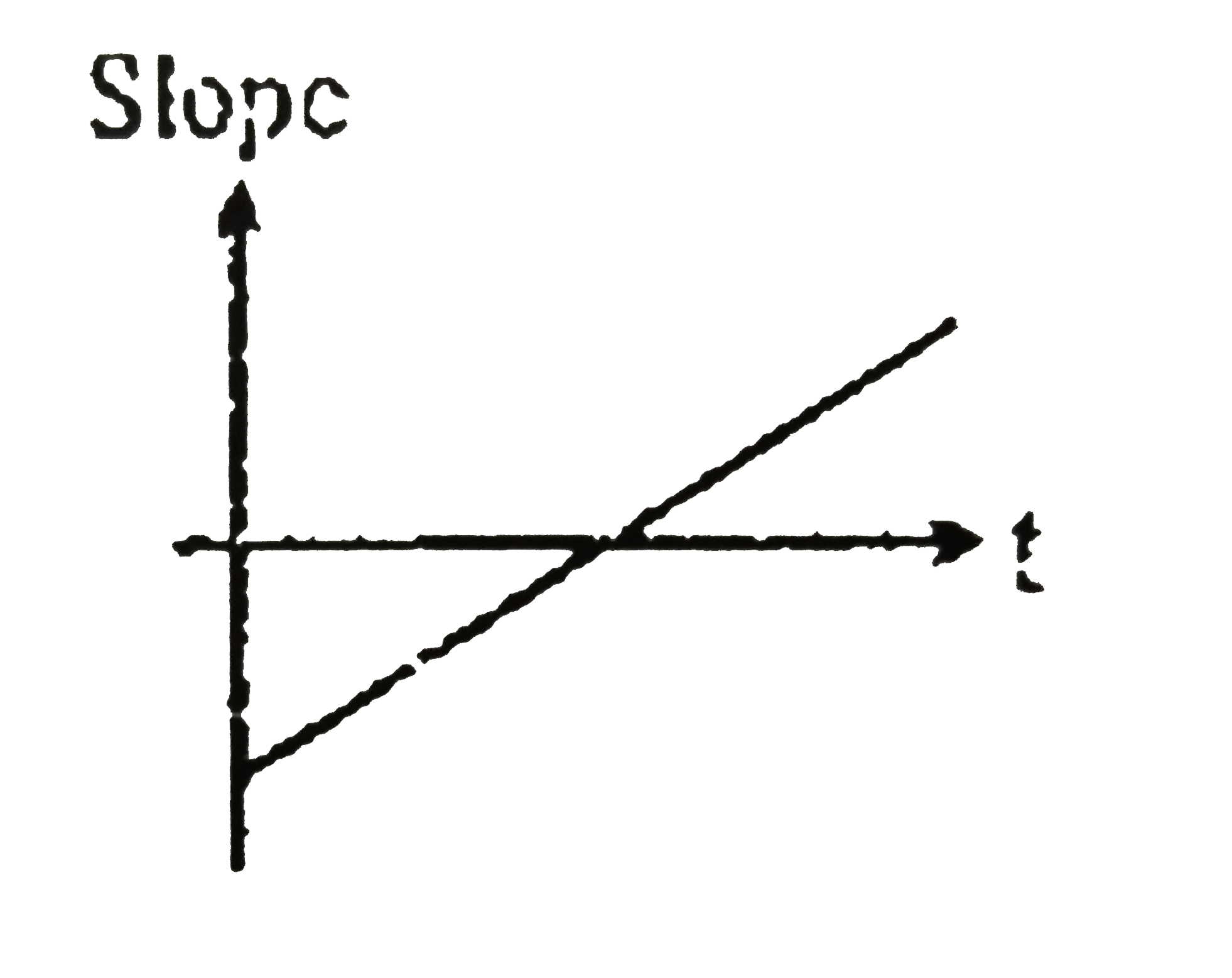
A particle is projected with a velocity '9m/sec' at an angle 450, with the horizontal.What is the radius of curvature of the trajectory of the particle at the position 'x=R/3' (R-Range of the projectile).
A3√20mB3√10C3√102mD34√10mA particle is projected with a velocity 8m/sec at an angle 450, with the horizontal.What is the radius of curvature of the trajectory of the particle at the instant of '14th' of the time of ascent.
A6.25mB12.5mC8mD10m
A particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View SolutionA particle is projeced with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View SolutionA particle is projected with initial velocity u making an angle α with the horizontal, its time of flight will be given by
View SolutionA particle is projected at angle θ with horizontal from ground. The slop (m) of the trajectory of the particle varies with time (t) as
View SolutionA particle is projected with speed u at angle θ to the horizontal. Find the radius of curvature at highest point of its trajectory
View Solution

