A diwali rocket moves vertically up with a constant acceleration a1=20//3ms−2. After sometives, its fuel gers exhausted ad then if falls freely with an acceleration a2=10ms−2, If themaximum height attained by the diwalin rocket is (h), using graphicalmerhod, find its speed when the fuel is just exausted. Assume h=50m.
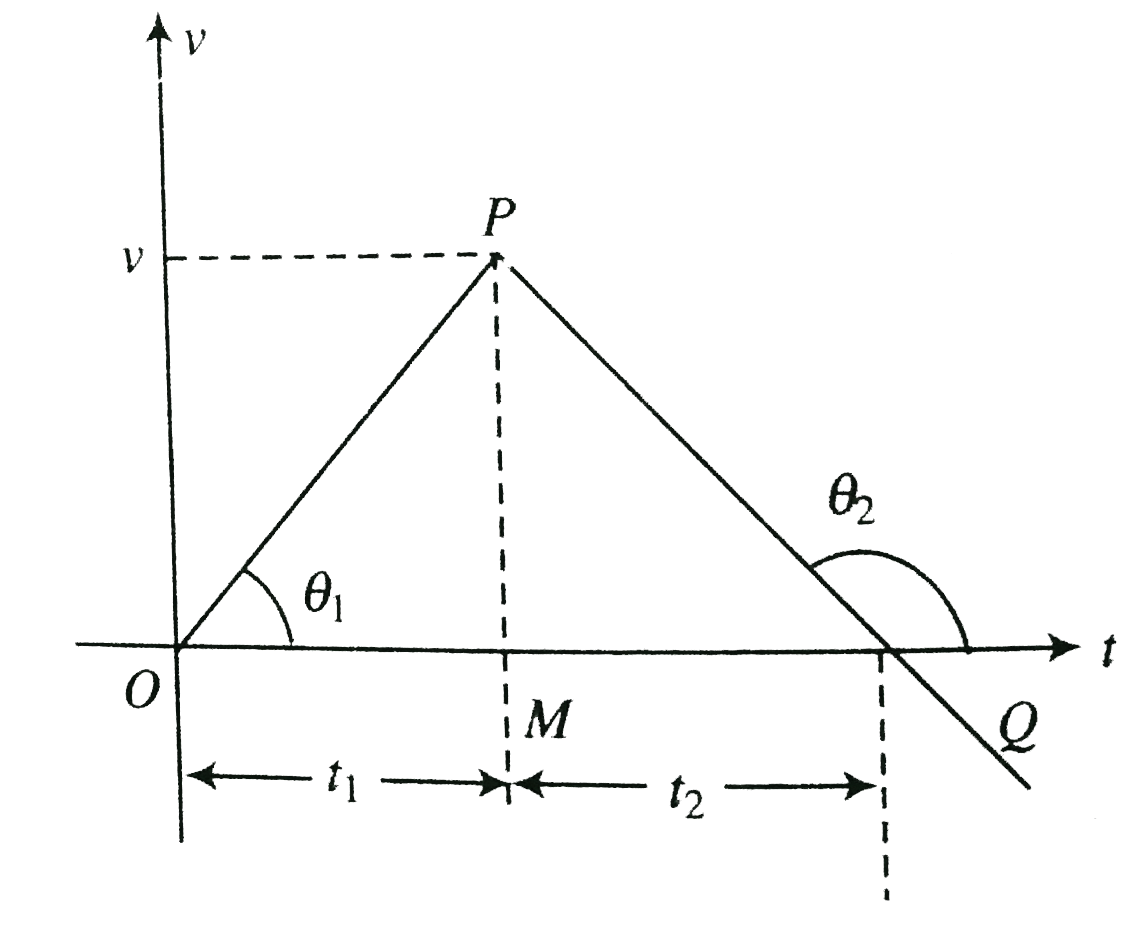
Let the rocket acquire a speed v at the time when all its fuel gets exhausted. Referring to the v−t graph in Fig. the slope of OP gives the acceleration a1.
 .
.
The slope of OP gives the acceleration a1=tanθ1=vt1
The slope of PQ gives the acceleraion
(−a2)=tanθ2=−vt(2)
From (i) and (ii), we have
v=a1t1=a2t2.
The area under v−t graph=Area ΔOPQ=12OQ.PM=s
Susbstituting OQ=t1+t2 and (t1+t2
Substituting t12=va1 and t2va2 from (iii) in (iv), we have
s=v2(va1+va2) Finally substituting s=+h (as the area is positive), a1=203ms−2
and a2=10ms−2, we have <br>v=sqrt((2a_(1)a_(2)h)/(a_(1)+a_(2)))=sqrt((2xx(20)/(3)xx10xx50)/((20)/(3)+10))<br>Thissieldsv=20 m s^(-1).
Topper's Solved these Questions
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Exercise 4.1
Explore 17 Videos
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Exercise 4.2
Explore 12 Videos
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Integer
Explore 9 Videos
Similar Questions
A rocket is fired vertically from the ground. It moves upwards with a constant acceleration 10m/s2 after 30 sec the fuel is finished. After what time from the instant of firing the rocket will attain the maximum height? g=10m/s2:-
View SolutionA rocket is fired upwards such that its engine takes 10 s to explods fully. Its velocity- time graph is as shown in the figure. Acceleration due to gravity is 10m/s2.

The maximum height attained by the rocket is
View Solution
Knowledge Check
A rocket is fired and ascends with constant vertical acceleration of 10m/s2 for 1 minute. Its fuel is exhausted and it continues as a free particle. The maximum altitude reached is (g=10m/s2)
A18 kmB36 kmC72 kmD108 kmA particle moves rectilinearly with a constant acceleration 1m/s2. Its speed after 10 seconds is 5m/s. The distance covered by the particle in this duration is.
A20 mB25 mC30 mD50 mA rocket is fired vertically upwards and moves with net acceleration of 10m/s2. After 1 min the fuel is exhausted. The time taken by it to reach the highest point after the fuel is exhausted will be:
A10 secB20 secC30 secD60 sec
A rocket is fired vertically up from the ground with an acceleration 10 m/s2. If its fuel is finished after 1 minute then calculate -
(a) Maximum velocity attained by rocket in ascending motion.
(b) Height attained by rocket fuel is finished.
(c ) Time taken by the rocket in the whole motion.
(d) Maximum height attained by rocket.
View SolutionA body moves from rest with a constant acceleration of 5m/s2. Its instantaneous speed (in m/s) at the end of 10 sec is
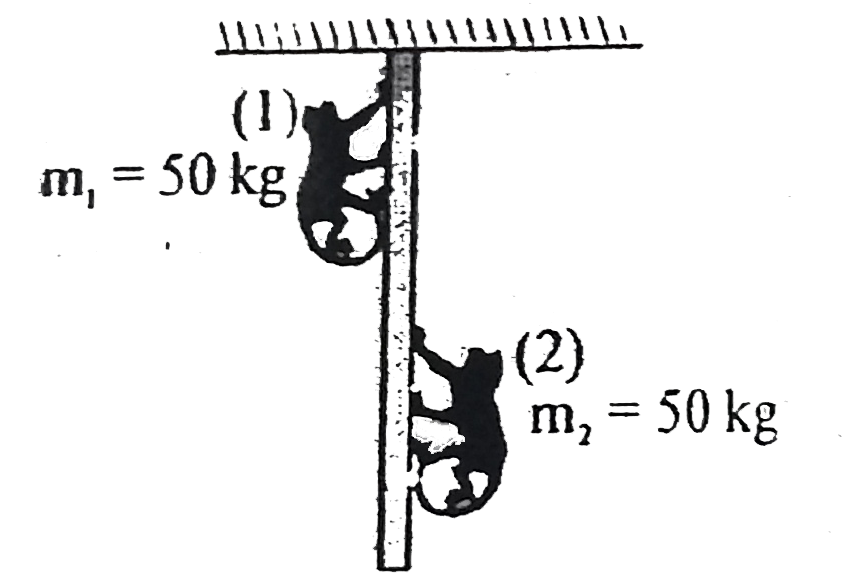
View SolutionMonkey (1) is climbing up a light rope with acceleration of a1=2m/s2 and monkey (2) is climbing upto the same rope with acceleration of a2m/s2 Choose incorrect options.
View SolutionA bus moving along a straight line at 20 m/s undergoes an acceleration of 4 m/s2. After 2 seconds, its speed will be :
View SolutionThe exhaust velocity of gases with respect to a small rocket of mass 25 kg. is 28×102m/s. At what rate the fuel must burn so that it may rise up with an acceleration of 9.8m/s2?
View Solution

