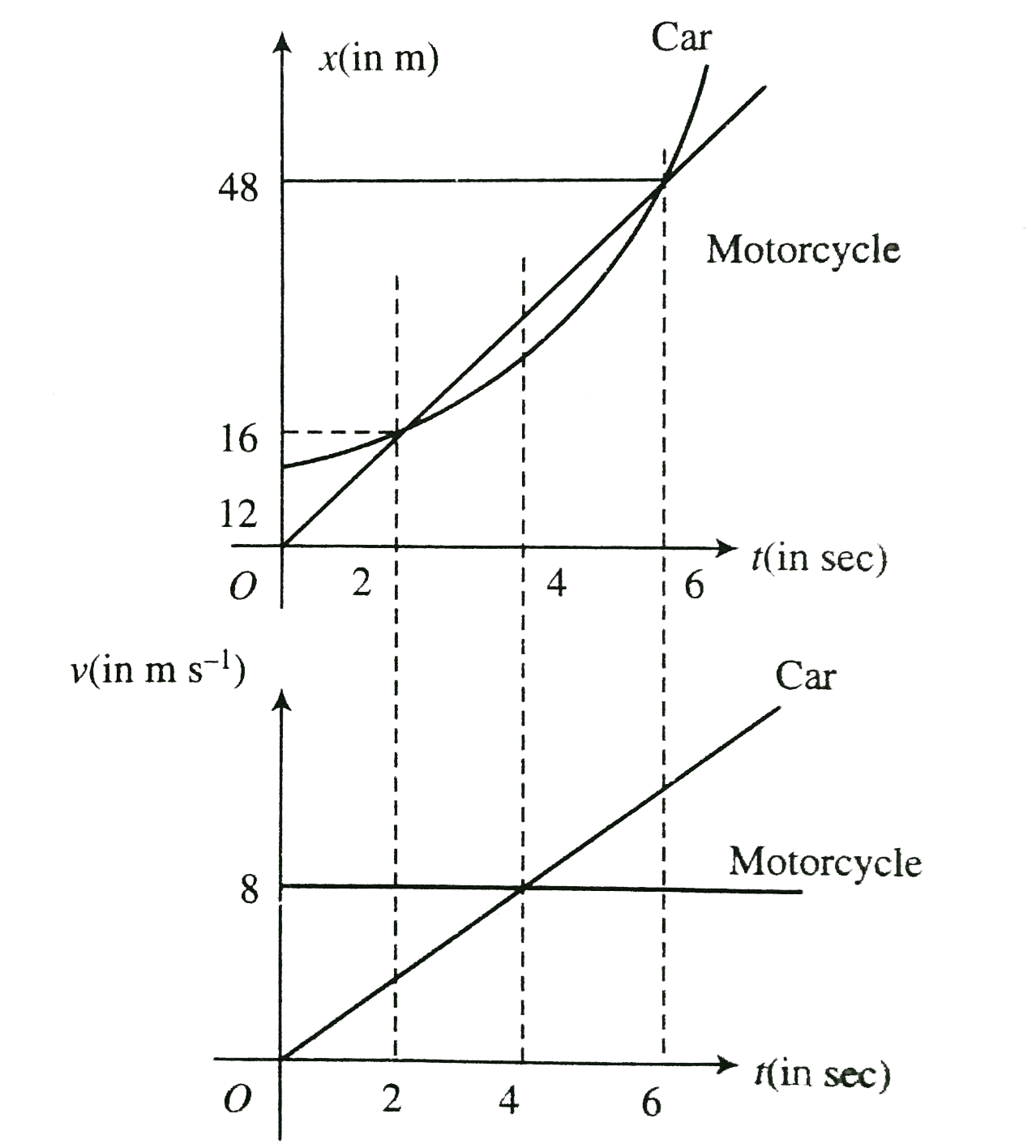
A motorcyclist situated at origin is located at a distance $12 m$ . Behind a car (Fig. 4.150).
.
At $t = 0$ the motorcyclist stars moving with a constant velocity $v = 8 m s^{- 1}$ and same time the car starts acceleration from rest with $a = 2 m s & (- 2)$ , (a) When and wher do they meet?

Video Solution

Text Solution

Verified by Experts

Let the car and motorcycle meet, after a time $t$ . During the time, the motorcycle comers a distance $d_{m}$ say. Position of motorcycle, $x_{m} = d_{m} = v t$ ..(i)
During the time $t$ the car moves through a distance
$d_{c} = \frac{1}{2} a t^{2}$
Position of car, $x_{c} = 12 + d_{c} = 12 + \frac{1}{2} a t^{2}$ ...(ii)
When both motorcycle and car meet their positions will be same.
From (i) and (ii) $x_{m} = x_{c}$ .
We have $v t = 12 + \frac{1}{2} a t^{2}$
Then substituting $v = 8 m s^{- 1}$ and $a = 2 m s^{- 2}$ , We have
$r^{2} - 8 t + 12 = 0$
.
This yields two real values of time, i.e., $t - 2 s$ and $6 s$ .
The following conclusion can be made from the above mathematical proceedings.
At t=2 s $t h e m o \to r c y c \leq a p p r o a c h e s t h e c a r . < b r > T h e p o s i t i o n o f m o \to r c y c l i s t < b r >$ (x_(m))_(t=2s)=8 xx2 =16 m $< b r > A t$ t=6 s $, t h e c a r o v e r t a k e s t h e m o \to r c y c \leq . < b r > A t$ t=2 s $, t h e m o \to r c y c \leq o v e r t a k e s t h e c a r . T h e i t \div e r \geq s (m o v e s a w a y o m t h e c a r) t i l l t h e a c q u i r e s a v e l o c i t y e q u a l \to t ˆ o f m o \to r c y c \leq a t$ t=4 s. Then the distance jof separation will gradually decreases as the car moves faster than the motorcycle. After that, the car will take a lead leaving the motorcyle behind it.

Updated on:21/07/2023

A cyclist starts from rest and moves with a constant acceleration of 1 $m / s^{2}$ . A boy who is 48 m behind the cyclist starts moving with a constant velocity of $10 m / s$ . After how much time the boy meets the cyclist?
A $8 s$
B $12 s$
C $10 s$
Dboth 1 and (2)
Two cars A and B are at rest at the origin O. If A starts with a uniform velocity of $20 m /$ s and $B$ starts in the same direction with a constant acceleration of $2 m / s^{2}$ , then the cars will meet after time
A $10 s$
B $20 s$
C $30 s$
D $40 s$
In the previous problem if the car is moving with a constant acceleration of $2 m / s^{2}$ , the ball will fall behind the person at a distance
A $32 m$
B $64 m$
C $96 m$
D $16 m$