(a) Show that the velocity acquired by a particle in sliding down an inclined plane is the same as that acquired by a particle falling freely from frst though a distance equal to the height of the inclined plane. (b) Find the time taken in sliding a particle down the whole length of the incline.
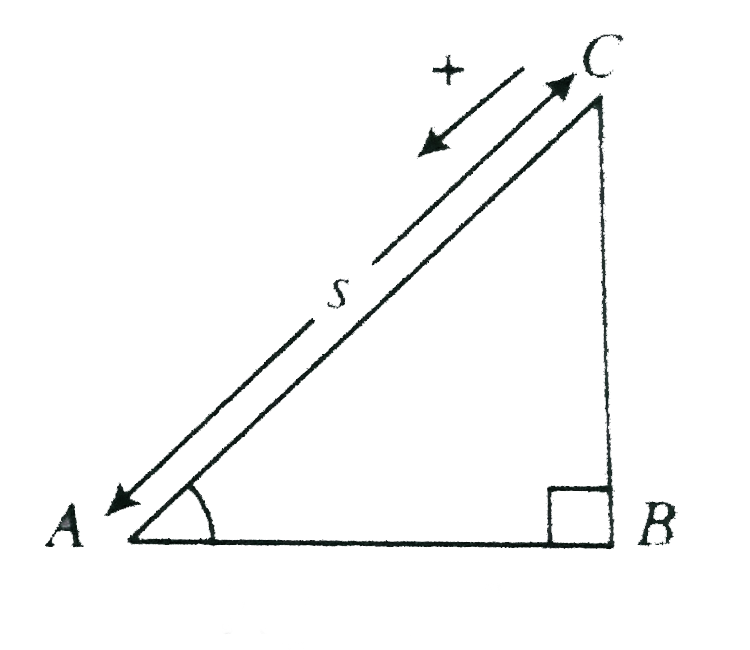
Let a particle sliding from c to A along the inclined planceCA acquire a final velocity v1, comering a distance s .
If θ is the angle of inlination, then
sinθ=hs
 .
.
Now for the sliding particle, s=s,u=0,a=gsinθ,v=v1.
[Taking the direction C to A as positive]
Using, v2u2+2as
⇒v21=2(gsinrhη)s=2g[hs]s=2gh
becuasev1=√2gh
Again, let aparticle fall from rest along a distance h and acquire a velocity v2, then from v2=u2+2as,
v22=0+2gh⇒v2=√2gh (ii)<br>From(i)and(ii),we≥tthesamerest–.<br>b.Timetake∈slgapartic≤downtheentire≤n>hofthe∈cl∈e:<br>Forthemotionofpartic≤omC→Au=0,<br>s=s, a=g sin theta, t=?.<br>Usings=ut+(1)/(2) a t^(2),we≥ts=(1)/(2)(g sin theta) t^(2)<br>rArr (t^(2)=(2s)/(g sin theta)=(2h)/(g sin^(2) theta)[becuasesinθ=hs]<br>becuase t= sqrt(2h)/(g) cos theta<br>Thus,thetimetakevariesdirectlyadthecosecantofthe∠of∈cliation.Now,sincecosecantisadectrasingfunction∈thefirst rantwithan∈crease∈thetatimet would decrease.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Solved Examples
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A particle slides down a smooth in clined plane of elevation θ fixed in an elevastor going up with an accelerationa0. The base of the incline has a length L.Find the time taken by the particle to reach the bottom.
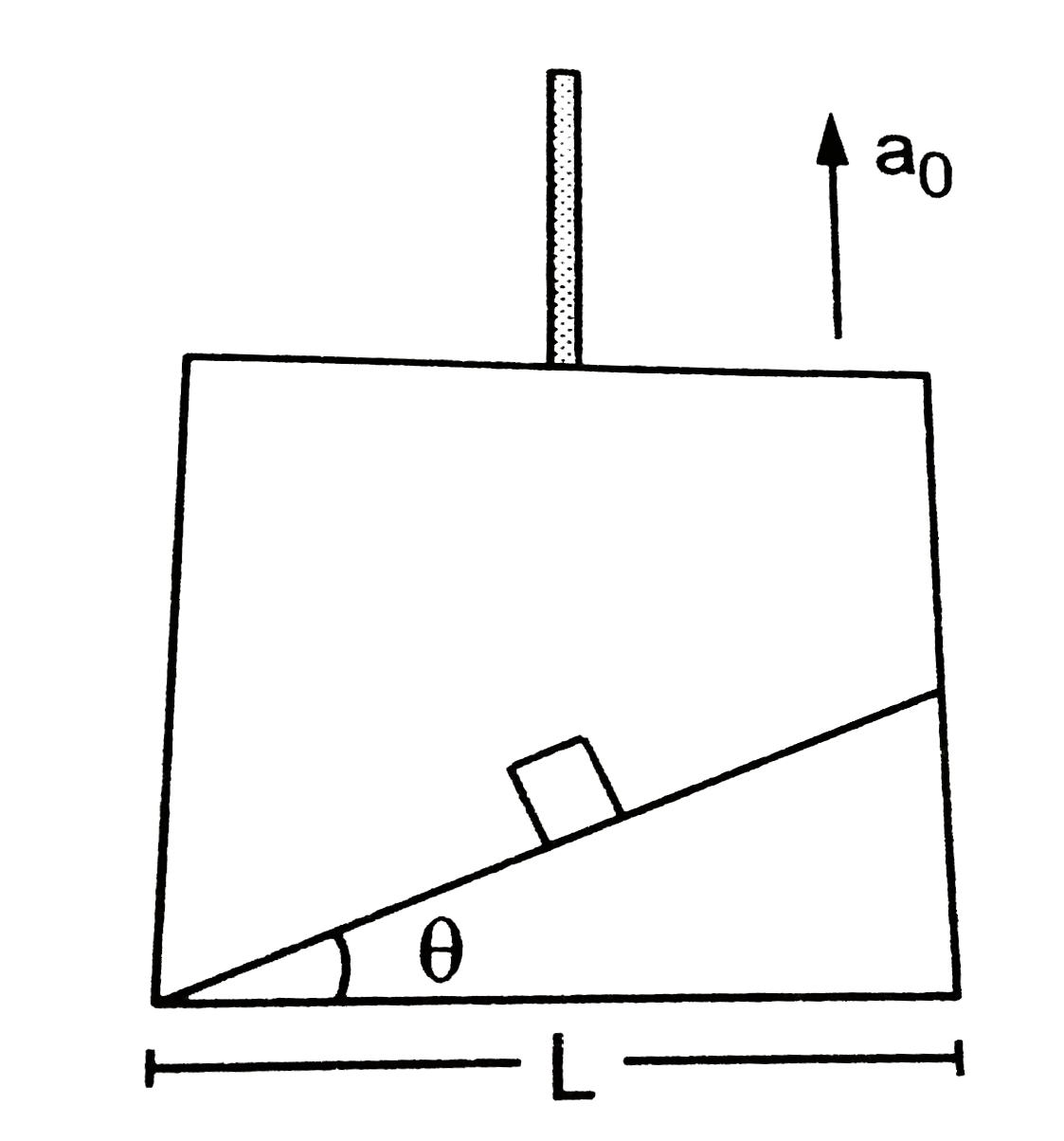
View SolutionA particle slides down a smooth inclined plane of elevation θ fixed in a elevator going up with an acceleration a0. The base of the inline has a length L.
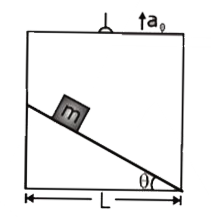
View Solution
Knowledge Check
The time taken by a particle to slide down a smooth inclined plane is double the time it would take in falling down through a height equal to the vertical height of the plane. The inclination of the plane with horizontal is :
A30∘B45∘C60∘D90∘An object start sliding on a frictionless inclined plane and from same height another object start falling freely
ABoth will reach with same speedBBoth will reach with same accelerationCBoth will reach in same timeDNone of aboveA block slides down a smooth inclined plane when released from the top, while another falls freely from the same point :
Asliding block will reach the ground first with greater speedBfreely falling block will reach the ground first with greater speedCboth the blocks will reach the ground at the same time but with different speedsDboth the blocks will reach the ground with same speed but the freely falling block first
A body sliding down on a smooth inclined plane slides down 1/4th distane in 2s. I will slide down the complete plane in
View SolutionA body is sliding down an inclined plane having coefficient of friction 0.5. If the normal reaction is twice that of resultant downward force along the inclined plane, then find the angle between the inclined plane and the horizontal .
View SolutionA particle slides down a smooth inclined plane of elevation , fixed in an elevator going up with an acceleration a0 (figure). The base of the incline has a length L. Find the time taken by the particle to reach to the bottom -

View SolutionA body is sliding down an inclined plane (μ=12). If the normal reaction is twice that of the resultant downward force along the incline , the inclination of plane is
View SolutionStarting from rest a body slides down a 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of the body and the inclined plane is :
View Solution
