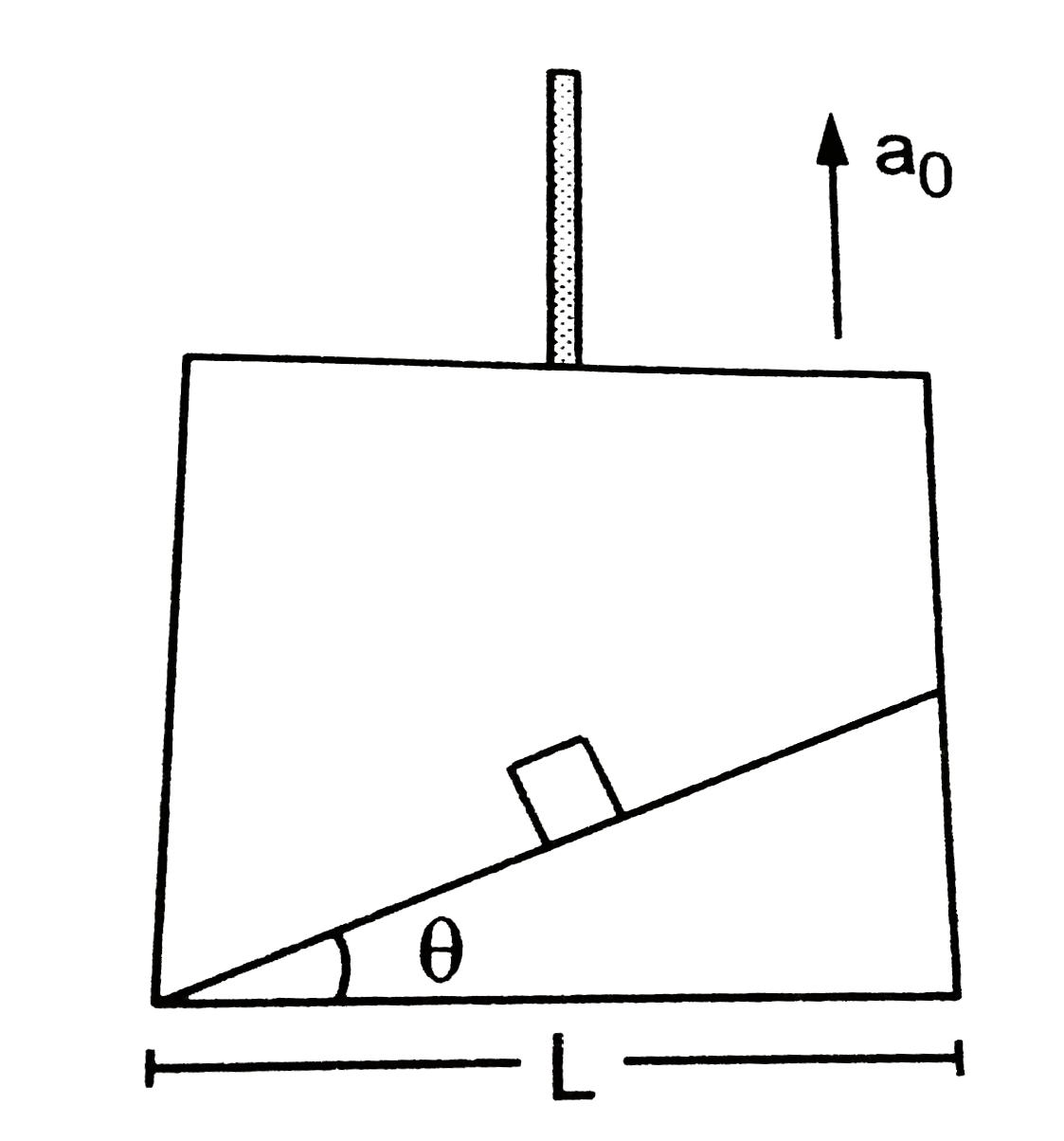
A particle slides down a smooth inclined plane of elevation , fixed in an elevator going up with an acceleration a0 (figure). The base of the incline has a length L. Find the time taken by the particle to reach to the bottom -

[2Lgsinθcosθ]1/2
[2L(g−a0)sinθcosθ]1/2
[2L(g+a0)cosθ]1/2
[2L(g+a0)sinθcosθ]1/2
The correct Answer is:D
Step by step video, text & image solution for A particle slides down a smooth inclined plane of elevation , fixed in an elevator going up with an acceleration a0 (figure). The base of the incline has a length L. Find the time taken by the particle to reach to the bottom - by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle slides down a smooth in clined plane of elevation θ fixed in an elevastor going up with an accelerationa0. The base of the incline has a length L.Find the time taken by the particle to reach the bottom.
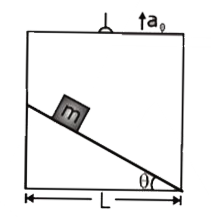
View SolutionA particle slides down a smooth inclined plane of elevation θ fixed in a elevator going up with an acceleration a0. The base of the inline has a length L.
View Solution
Knowledge Check
A particle slides down on a smooth incline of inclination 30∘, fixed in an elevator going up with an acceleration 2m/s2. The box of incline has width 4m. The time taken by the particle to reach the bottom will be
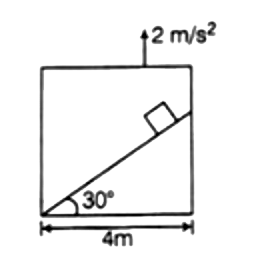 A89√3sB98√3sC43√√32sD34√√32s
A89√3sB98√3sC43√√32sD34√√32sA particle slides down a smooth inclined plane of elevation fixed in an elevator going with an acceleration a as shown in the figure. The base of the incline has a length L.
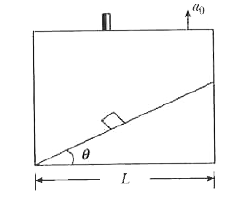
If the elevator going up with constant velocity, the time taken by the particle to reach the bottom isA(2L(gsinθcosθ))1/2B(2Lgsinθ)1/2C(2Lgcosθ)1/2DNone of theseA body of mass m is placed over a smooth inclined plane of inclination θ, which is placed over a lift which is moving up with an acceleration a0 . Base length of the inclined plane is L. Calculate the velocity of the block with respect to lift at the bottom, if it is allowed to slide down from the top of the plane from rest :-
A√2(a0+g)LsinθB√2(a0+g)LcosθC√2(a0+g)LtanθD√2(a0+g)Lcotθ
A particle slides down a smooth incline of inclination 37∘, fixed in an elevator going up with an acceleration (g)/3. The base of incline has a length 5m. Find the time taken by the particle to reach the bottom.
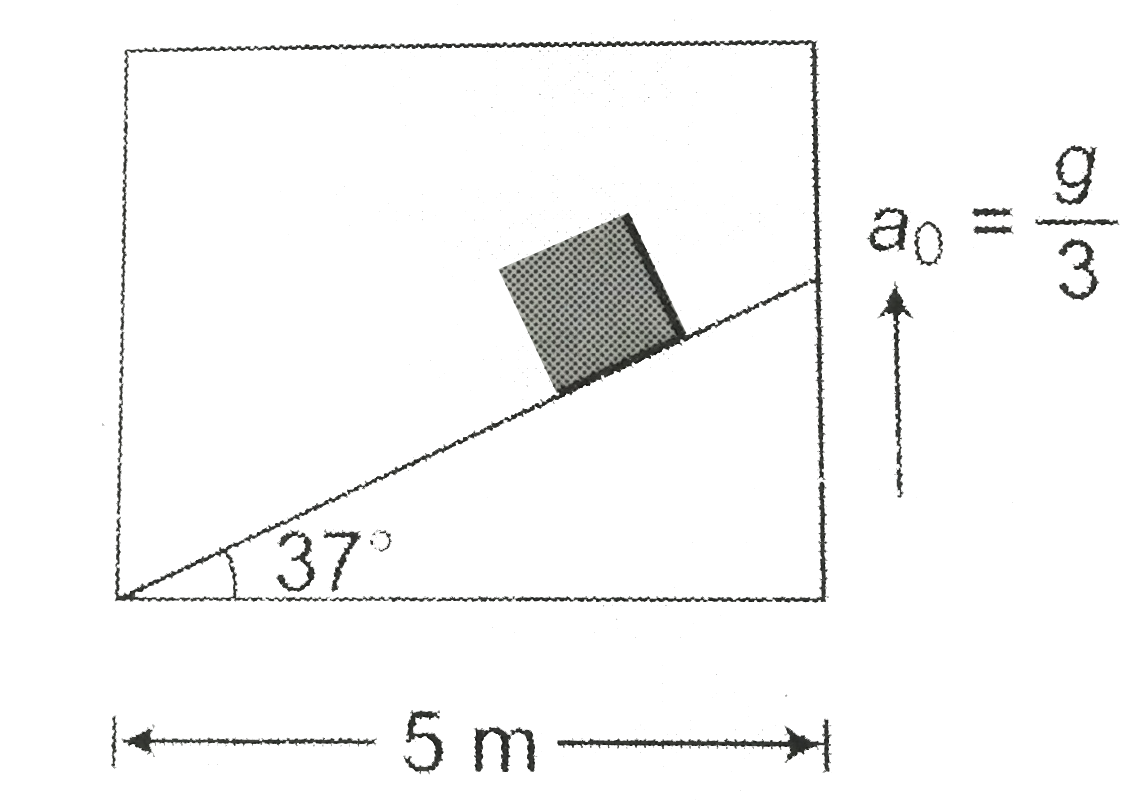
View SolutionA block slides down from top of a smooth inclined plane of elevation ● fixed in an elevator going up with an acceleration a0 The base of incline hs length L Find the time taken by the block to reach the bottom
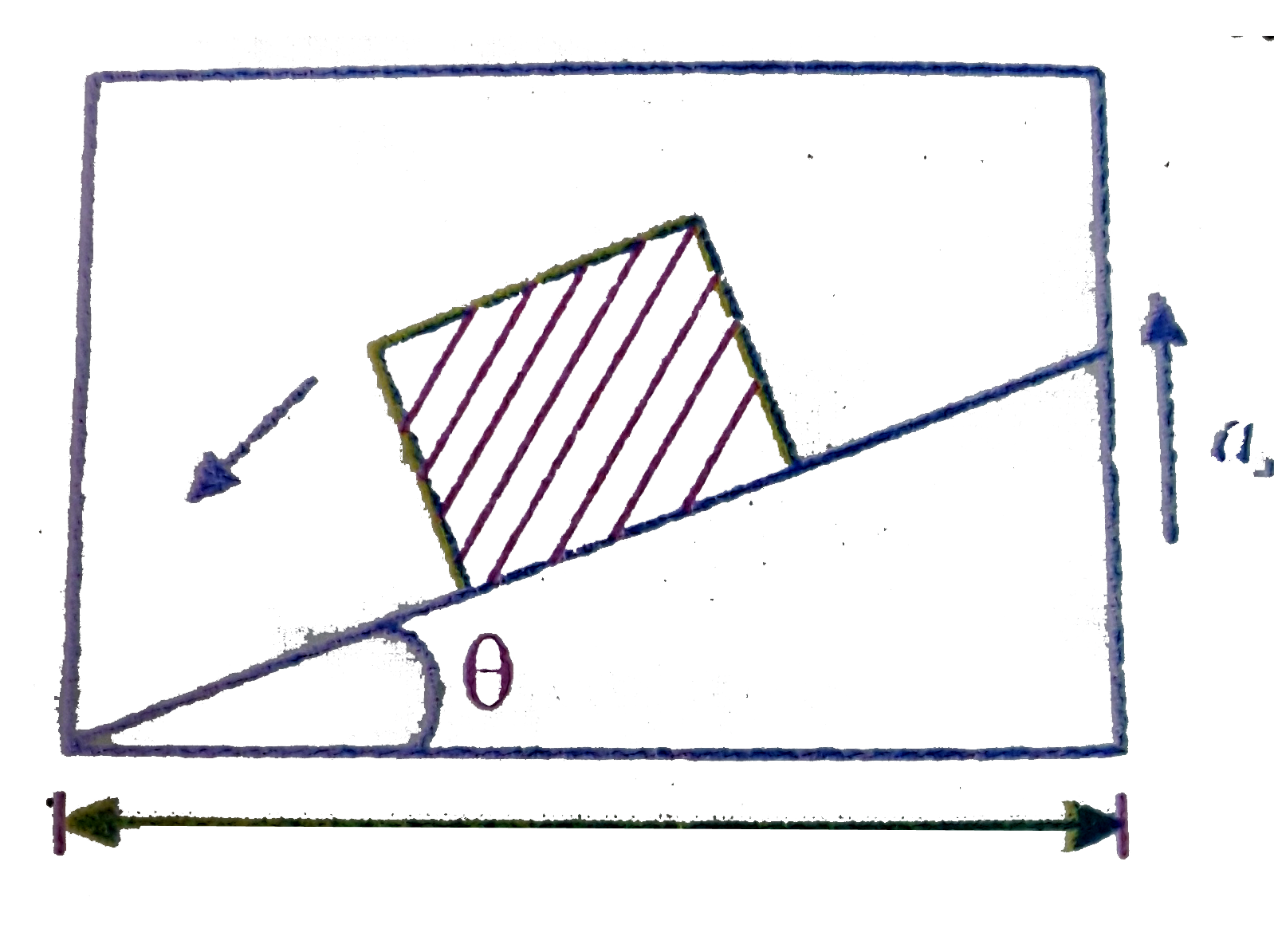 .
.
View SolutionA smooth wedge with elevation θ is fixed in an elevator moving up with uniform acceleration a0=g/2. The base of the wedge has a length L. Find the time taken by a particle sliding down the incline to reach the base.
View SolutionA block is placed on an inclined plane moving towards right with an acceleration a0=g The length of the inclined plane is l0. All the surfaces are smooth Find the time taken by the block to reach from bottom to top.
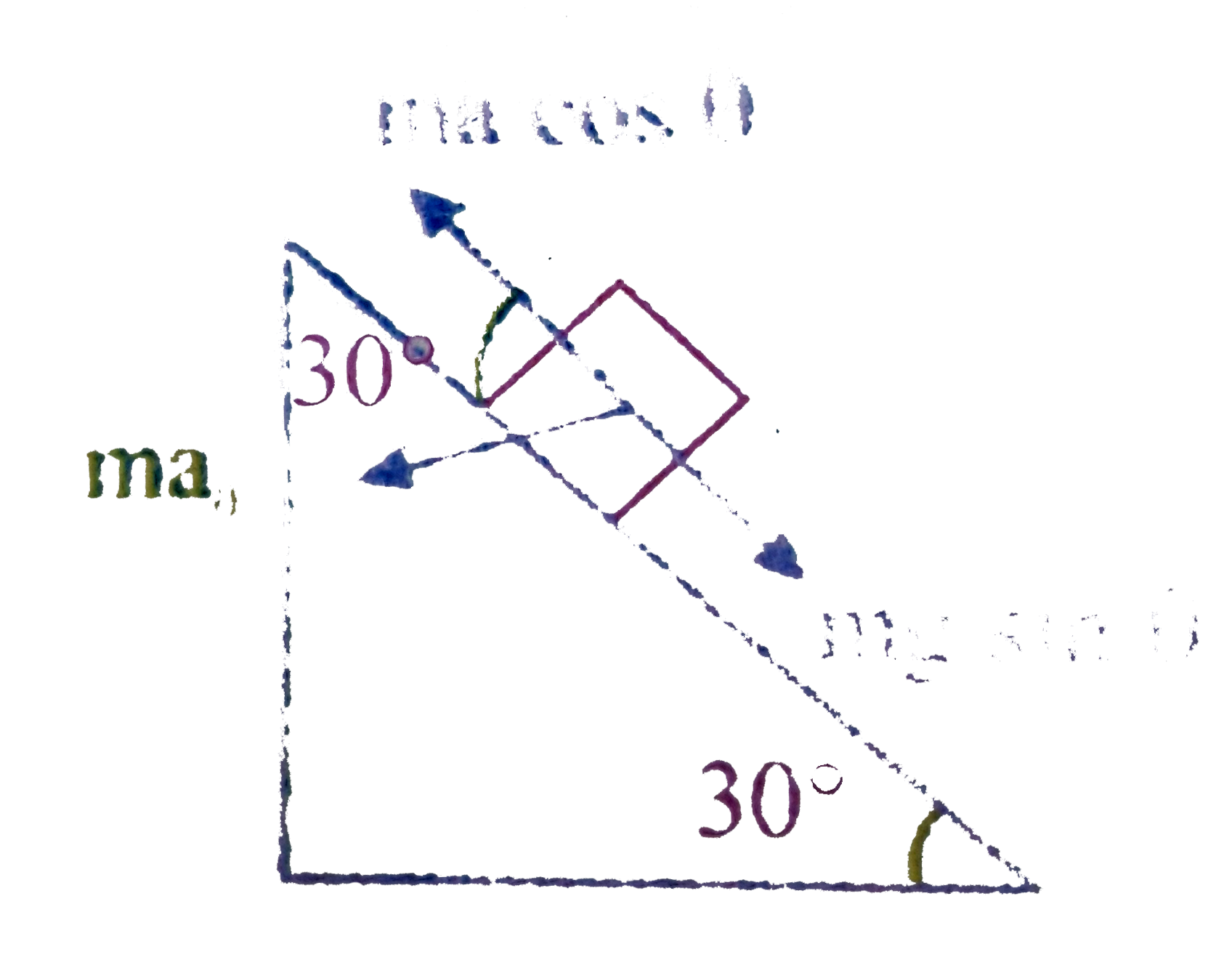 .
.
View SolutionA body of mass m is placed over a smooth inclined plane of inclination theta. Which iis placed over a lift which is moving up with an acceleration a0 . Base length o f the inclined plane is L . Calculate the velocity of the block with respect to lift at the bottom, if it is allowed to slide down from the top o fthe plane from rest.
View Solution

