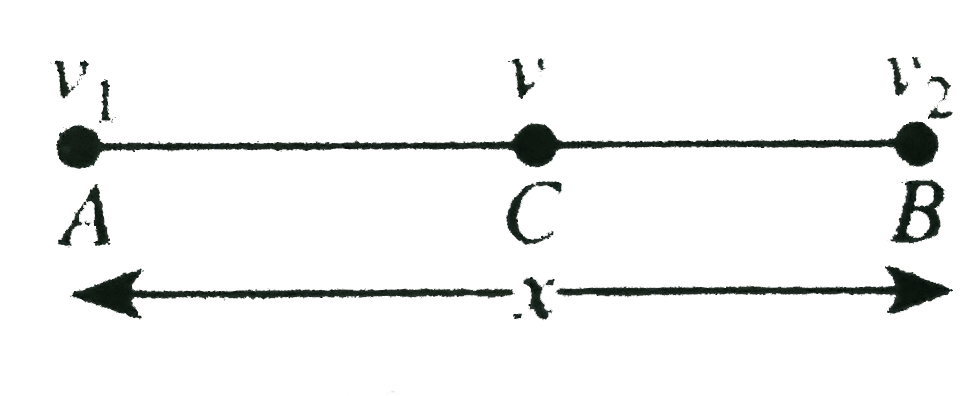
A particle moving with uniform acceleration from A to B along a straight line has velcities v1 and v2 at A and B respectively. If C is the mid-point between A and B then determine the velocity of the particle at C .
 .
.
Let v be the velocity of the particle at c. Assume the acceleration of the particle to be A and distance between A and B be x. To find the velocity c, consider the motion from Aand C:
Applying v2−u2=2 as, we get v2−v21=2ax2
⇒v2−v21=ax........ (i)
Appying the same equation from C to B. we get<br>V_(2)^(2)=2a(x)/(2) rArr v_(2)^(2)-v^(2)=ax......(ii)<br>From(i)and(ii),we≥tv=sqrt(v_(1)^(2)+v_(2)^(2))/(2).
Topper's Solved these Questions
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Solved Examples
Explore 9 Videos
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Exercise 4.1
Explore 17 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Integer
Explore 9 Videos
Similar Questions
(a) A particle moving with constant acceleration from A to B in a straight line AB has velocities u and v at A and B respectively. Find the velocity of the particle at the midpoint of AB.
(b) If the time taken by the particle to go from A to the midpoint of AB is two times that from the midpoint of AB to B then find the value of v/u.
View SolutionA particle is moving with uniform acceleration along a straight line "ABC" .Its velocity at A and B are 6m/s" and "9m/s respectively. If AB:BC=5:16" then its velocity at C is
View Solution
Knowledge Check
A particle is moving with uniform acceleration along a straight line ABC. Its velocity at A and B are 6 m/s and 9 m/s respectively if AB:BC=5:16 then its velocity at C is
A9.6m/s2B12m/sC15m/sD21.5m/sA body is moving with constant acceleration, a=5ms2 from A to B in straight line AB. The velocity of particle at A and B are 5 m/s and 15 m/s respectively. The velocity at mid-point of AB is
A√125msB√250msC√550msD√600msFor a body moving with uniform acceleration along straight line, the variation of its velocity (v) with position (x) is best represented by
A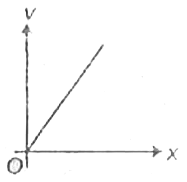 B
B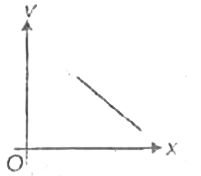 C
C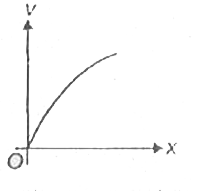 D
D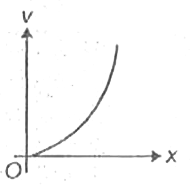
A point moving with constant acceleration from A to B in the straight line AB has velocities u and v at and B respectively. Find its velocity at C, the mid point of AB. Also show that if the time from A to C is twice that from C to B, then v=7u.
View SolutionA particle moving with a uniform acceleration along a straight line covers distances a and b in successive intervals of p and q second. The acceleration of the particle is
View SolutionA particle is executing SHM along a straight line. Its velocities at distances x1 and x2 from the mean position are v1 and v2, respectively. Its time period is
View SolutionA particle moves from A to B with a uniform velocity v1 and from B to A with a velocity v2. If it moves along a straight line between A and B, then the average velocity of the particle is
View Solutiona particle moving along a straight line with uniform acceleration has velocities 7m/s at A and 17m/s at C. B is the mid point of AC. Then :-
View Solution

