(a) A particle moving with constant acceleration from $A$ to $B$ in a straight line $A B$ has velocities $u$ and $v$ at $A$ and $B$ respectively. Find the velocity of the particle at the midpoint of $A B$ .
(b) If the time taken by the particle to go from $A$ to the midpoint of $A B$ is two times that from the midpoint of $A B$ to $B$ then find the value of $v / u$ .

Video Solution

Text Solution

Verified by Experts

(a)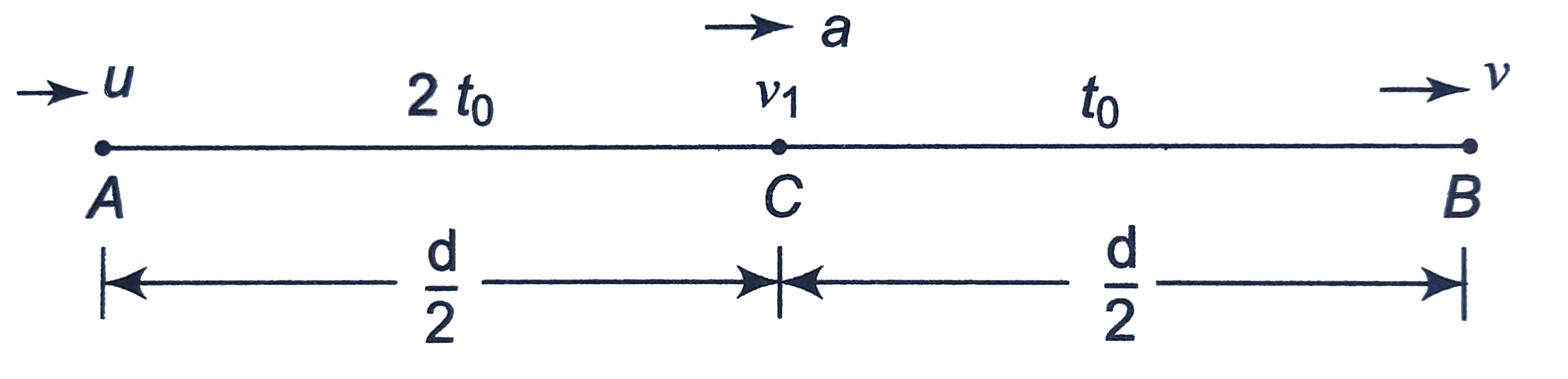
C: Midpoint of $A B$
$v_{1}$ : Velocity at $C$
$A$ to $C : v_{1}^{2} = u^{2} + 2 a . \frac{d}{2} \dots (i)$
$A$ to $B : v^{2} = u^{2} + 2 a d (i i)$
From (i) and (ii), we get
$\frac{v_{1}^{2} - u^{2}}{v^{2} - u^{2}} = \frac{a d}{2 a d} = \frac{1}{2}$
$2 v_{1}^{2} = v^{2} + u^{2}$
$v_{1} = \sqrt{\frac{v^{2} + u^{2}}{2}}$
(b) $A$ to $C : v_{1} = u + a .2 t_{0} \Rightarrow v_{1} - u = 2 a t_{0} ... (i)$
Ato $B : v = u + a .3 t_{0} \Rightarrow v - u = 3 a t_{0} ... (i i)$
Dividing (i) by (ii), we get
$\frac{v_{1} - u}{v - u} = \frac{2}{3} \Rightarrow 3 v_{1} - 3 u = 2 v - 2 u$
$v_{1} = \frac{2 v + u}{3} \Rightarrow \sqrt{\frac{v^{2} + u^{2}}{2}} = \frac{2 v + u}{3}$
squaring we get
$\frac{v^{2} + u^{2}}{2} = \frac{4 v^{2} + u^{2} + 4 v u}{9}$
$9 v^{2} + 9 u^{2} = 8 v^{2} + 2 u^{2} + 8 u v$
$v^{2} - 8 u v + 7 u^{2} = 0$
$(v - u) (v - 7 u) = 0 \Rightarrow v = u$ , not possible
$v = 7 u \Rightarrow \frac{v}{u} = 7$

Updated on:21/07/2023

A body is moving with constant acceleration, $a = 5 \frac{m}{s^{2}}$ from A to B in straight line AB. The velocity of particle at A and B are 5 m/s and 15 m/s respectively. The velocity at mid-point of AB is
A $\sqrt{125} \frac{m}{s}$
B $\sqrt{250} \frac{m}{s}$
C $\sqrt{550} \frac{m}{s}$
D $\sqrt{600} \frac{m}{s}$
A particle is moving with uniform acceleration along a straight line ABC. Its velocity at A and B are 6 m/s and 9 m/s respectively if $A B : B C = 5 : 16$ then its velocity at C is
A $9.6 m / s^{2}$
B $12 m / s$
C $15 m / s$
D $21.5 m / s$
Time taken by the particle to reach from $A$ to $B$ is $t$ . Then the distance $A B$ is equal to

A $\frac{u t}{\sqrt{3}}$
B $\frac{\sqrt{3} u t}{2}$
C $\sqrt{3} u t$
D $2 u t$