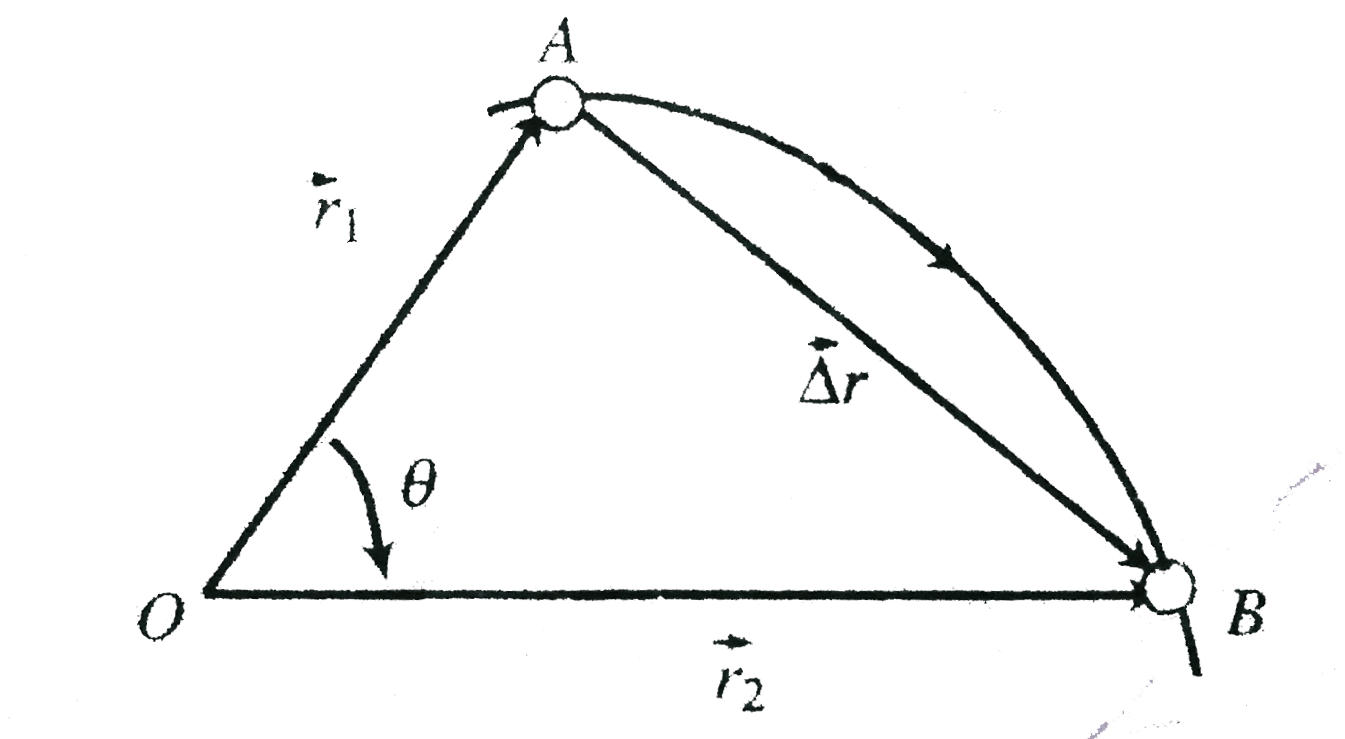
A particle moves from position to position in a path as shown in If the poit vectors and making an angle between them are give, find the magnitude of displacement.
 .
.
From triangle OAB:
Hence,
Topper's Solved these Questions
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Solved Examples
Explore 9 Videos
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Exercise 4.1
Explore 17 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Integer
Explore 9 Videos
Similar Questions
Find the magnitude of each of the two vectors →a and →b having the same magnitude such that the angle between them is 60∘ and their scalar product is 9/2.
View SolutionFind the magnitude of two vectors →a and →b having the same magnitude and such that the angle between them is 600 and their scalar product is .
View Solution
Knowledge Check
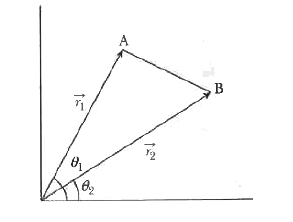
In a two-dimensional motion of a particle, the particle moves from point A of position vector →r1, to point B of vectors are , respectively, r1=3andr2=4 and the angles they make with the x axis are θ1=75∘andθ2=15∘, respectively, then find the magnitude of the displacement vector.
 A15B√13C17D√15
A15B√13C17D√15If →e1 and →e2 are two unit vectors and θ is the angle between them, then sin(θ2) is:
A12|→e1+→e2|B12|→e1−→e2|C→e1.→e22D|→e1×→e2|2|→e1||→e2|In a two diamensional motion of a particle, the particle moves from point A, with position vector →r1 to point B, with position vector →r2. If the magnitudes of these vectors are, respectively, r1=3 and r2=4 and the angles they make with the x-axis are θ1=75∘ and θ2=15∘, respectively, then find the magnitude of the displacement vector.
 A15B√13C17D√15
A15B√13C17D√15
Two particles 1and2 move with velocities →v1 and →v2 making the angles θ1andθ2 with the line joining them, respectively. Find angular velocity of relative→1.
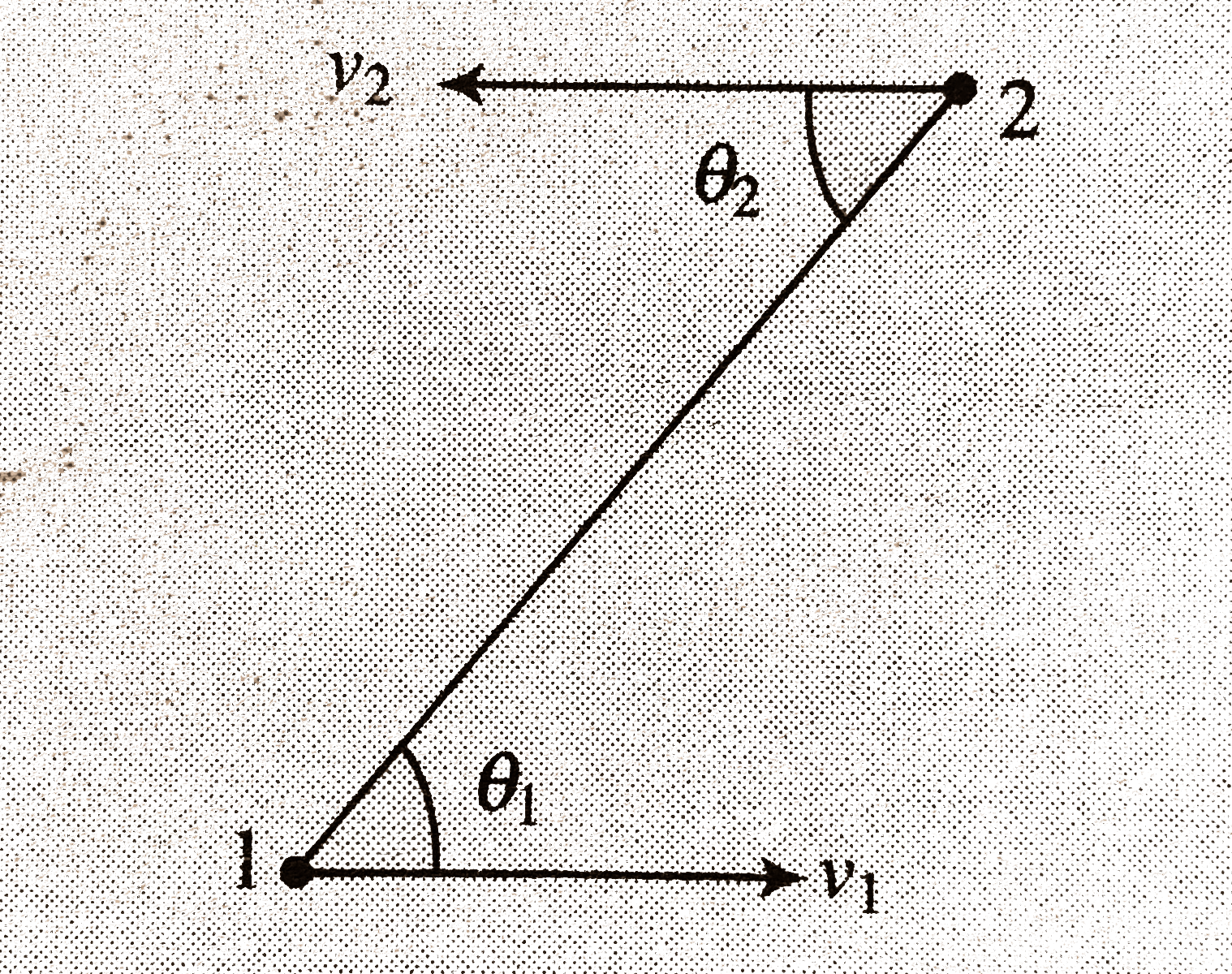 .
.
View SolutionA vector →r is inclined at equal angle to the three axes. If the magnitude of →r is 2√3, find →r.
View SolutionIf →a and →b are unit vectors, and θ is the angle between them, then ∣∣→a−→b∣∣ =
View SolutionFind the position vector of a point which divides the join of points with position vectors →a−2→b and 2→a+→b externally in the ration 2:1.
View SolutionA particle moves from A to B in a circular path of radius R covering an angle θ as shown in figure. Find the ratio of magnitude of distance and magnitude of displacement of the particle.

View Solution

