If the measured value of resistance R=1.05Ω, wire diameter d=0.60mm , and length l=75.3cm, then find the maximum permissible error in resistivity ,
ρ=R(πd2/4)l.
(dρρ)max=ΔRR+2Δdd+Δll
R=1.05Ω→ΔR=0.01Ω( least count)
Δd=0.60mm→Δd=0.01mm( least count)
l=75.3→Δl=0.1cm ( least count )
(dρρ)max=0.01Ω1.05Ω+2(0.01mm0.60mm)+0.1cm75.3cm
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Exercise 1.1
Explore 16 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Exercise 1.2
Explore 6 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
If measured value of resistance R=1.05Ω wire diameter d=0.60mm and length l=75.3cm If maximum error in resistance measurment is 0.01Ω and least count of diameter and length measuring device are 0.01mm and 0.1cm respectively then find max permissible error in resistiviry ρ=R(πd24)l .
View SolutionIn the experiment of Ohm's law, when potential difference of 10.0 V is applied, current measured is 1.00 A. If length of wire is found to be 10.0cm and diameter of wire 2.50 mm, then find maximum permissible percentage error in resistivity.
View Solution
Knowledge Check
The relative error in resistivity of a material where
resistance = 1.05 + 0.01 W
diameter = 0.60 + 0.01 mm
length = 75.3 + 0.1 cm isA0.04B0.40C0.08D0.01A wire of length l=6±0.06cm and radius r=0.5±0.005cm and m=0.3±0.003g. Maximum percentage error in density is:
A4B2C1D6A wire of length l=6±0.06cm and radius r=0.5±0.005cm and mass m=0.3±0.003g. Maximum percentage error in density is :
A4%B2%C1%D6.8%
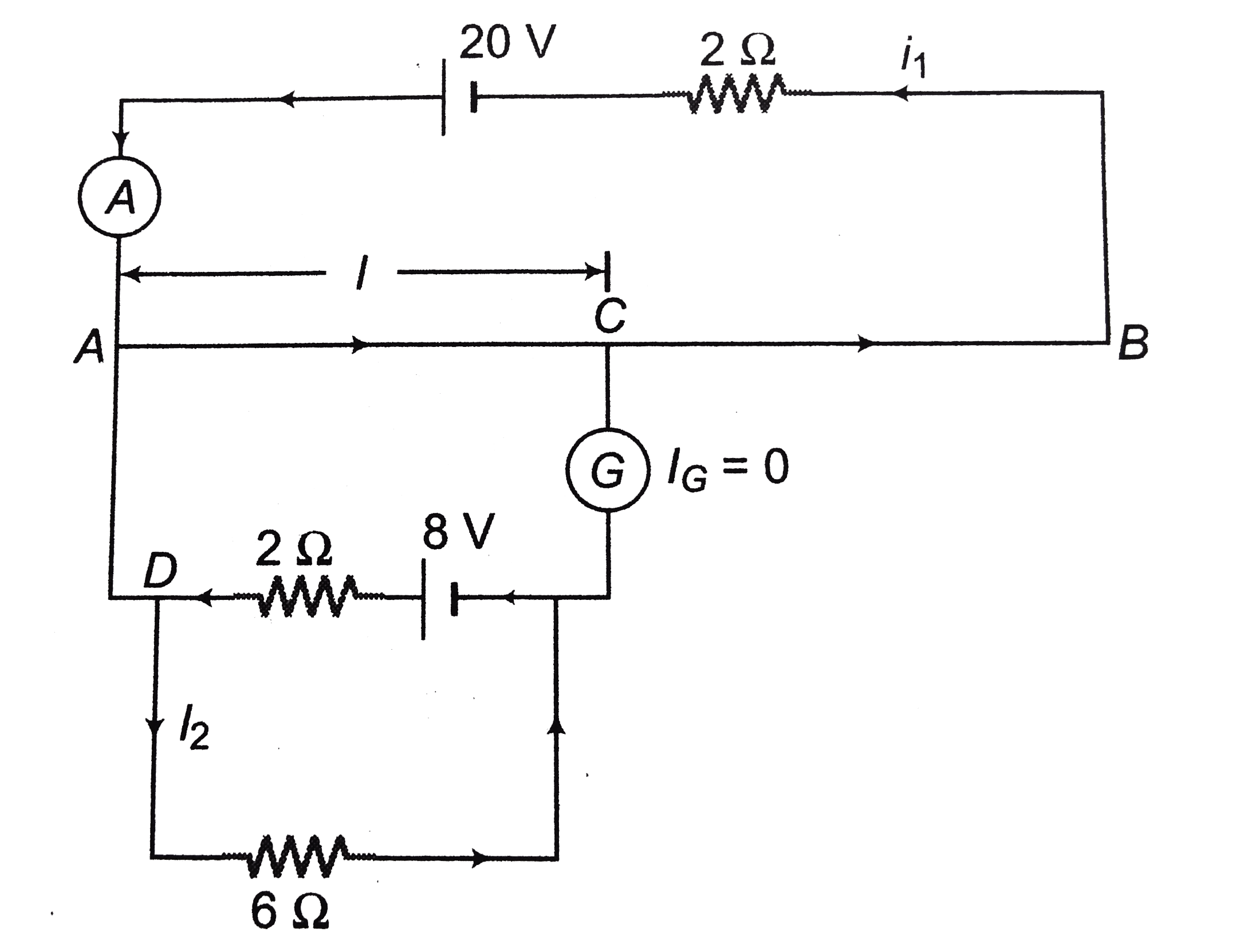
In the figure shown wire AB has a length of 100cm and resistance 8Ω. Find the balance point length l.
View SolutionThe resistance of a wire of uniform diameter d and length L is R . The resistance of another wire of the same material but diameter 2d and length 4L will be
View SolutionFor finding the specific resistance of a wire, a student took the following readings by using a metre scale, a micrometer and a resistance box.
Length of the wire (L) = 100.0 cm
Radius (r ) = 0.100 cm and R = 10Ω
What is the maximum possible percentage error in the value of the specific resistance?
View SolutionThe inductance L of a solenoid of length l, whose windings are made of material of density D and resistivity ρ, is (the winding resistance isR)
View SolutionIn Searle's exp to find Young's modulus, the diameter of wire is mesured as D=0.05cm length of wire is L=125cm, and when a weight, m=20.0kg is put, extension in wire was found to be 0.100cm. Find maximum permissible percentage error in Young's modulus (Y)
View Solution

