The resistance of a wire of uniform diameter d and length L is R . The resistance of another wire of the same material but diameter 2d and length 4L will be
2R
R
R/2
R/4
The correct Answer is:B
To find the resistance of the second wire, we can use the formula for resistance:
R=ρLA
where:
- R is the resistance,
- ρ is the resistivity of the material (constant for the same material),
- L is the length of the wire,
- A is the cross-sectional area of the wire.
Step 1: Identify the parameters for both wires
- For the first wire:
- Length L1=L
- Diameter d1=d
- Cross-sectional area A1=π(d2)2=πd24
- For the second wire:
- Length L2=4L
- Diameter d2=2d
- Cross-sectional area A2=π(2d2)2=πd2
Step 2: Write the resistance formulas for both wires
- Resistance of the first wire:
R1=ρL1A1=ρLπd24=4ρLπd2
- Resistance of the second wire:
R2=ρL2A2=ρ(4L)πd2=4ρLπd2
Step 3: Compare the resistances
From the calculations, we see that:
R1=4ρLπd2
R2=4ρLπd2
Step 4: Conclusion
Since R1=R2, we conclude that the resistance of the second wire is the same as that of the first wire:
R2=R
Final Answer
The resistance of the second wire is R.
---
- R is the resistance,
- ρ is the resistivity of the material (constant for the same material),
- L is the length of the wire,
- A is the cross-sectional area of the wire.
- For the first wire:
- Length L1=L
- Diameter d1=d
- Cross-sectional area A1=π(d2)2=πd24
- Length L2=4L
- Diameter d2=2d
- Cross-sectional area A2=π(2d2)2=πd2
- Resistance of the first wire:
R1=ρL1A1=ρLπd24=4ρLπd2
R2=ρL2A2=ρ(4L)πd2=4ρLπd2
From the calculations, we see that:
R1=4ρLπd2
R2=4ρLπd2
Since R1=R2, we conclude that the resistance of the second wire is the same as that of the first wire:
R2=R
The resistance of the second wire is R.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ERRORLESS CHAPTER - CURRENT ELECTRICITYEXERCISE - Kirchhoff s Law, cells
8 Videos
- CURRENT ELECTRICITYBOOK - ERRORLESS CHAPTER - CURRENT ELECTRICITYEXERCISE - Different Measuring Instruments
1 Videos
- COMMUNICATION SYSTEMBOOK - ERRORLESS CHAPTER - COMMUNICATION SYSTEMEXERCISE - S E T
14 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - ERRORLESS CHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - SET
20 Videos
Similar Questions
A cylindrical wire of length L and radius r has a resistance R. The resistance of another wire of the same material but half its length and half its radius will be:
View SolutionThe resistivity of wire made up of copper having length L and radius r is x.If another wire made up of same material but length 2L and radius r2 then its resistivity will be
View Solution
Knowledge Check
The breaking force for a wire of diameter D of a material is F. The breaking force for a wire of the same material of radius D is
AFB2FCF4D4FA mete bridge is used to determine the resistance of an unknown wire by measuring the balance point length l. If the wire is replaced by another wire of same material but with double the length and half the thickness the balancing point is expected to be
A18lB14lC8lD16lThe resistance of a wire of length l and diameter d is R. The wire is stretched to double its length. The resistance of the wire will now be
AR2B2RC4RD16R
A wire 50cm long and 0.12mm diameter has a resistance of 4.0Ω find the resistance of another wire of the same material whose length is 1.5m and diameter is 0.15mm
View SolutionA certain wire has a resistance R . The resistance of another wire identical with the first except having twice its diameter is
View SolutionA force F is applied on the wire of radius r and length L and change in the length of wire is l. If the same force F is applied on the wire of the same material and radius 2r and length 2L. Then the change in length of the other wire is
View SolutionThe resistance of a wire is 10−6Ω per metre. It is bend in the form of a circle of diameter m 2 . A wire of the same material is connected across its diameter. The total resistance across its diameter AB will be
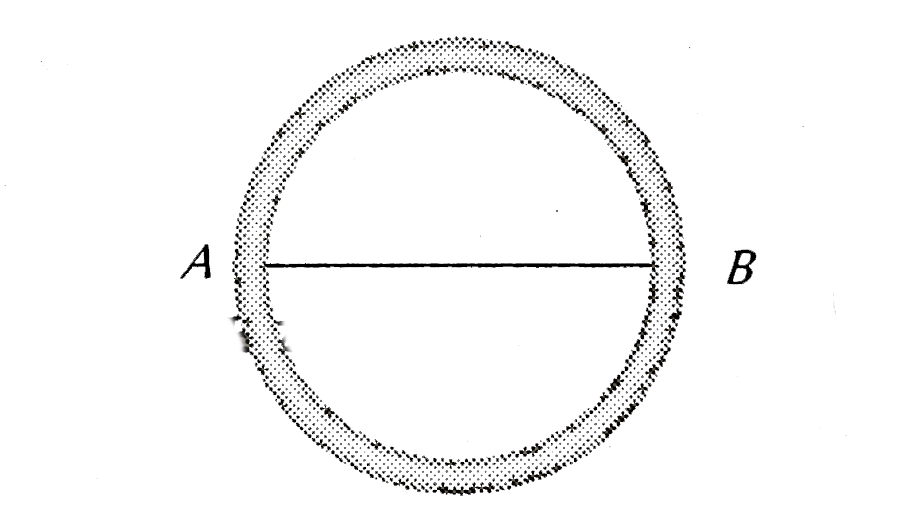
View SolutionThe resistance of a wire is 10 ohm. The resistance of a wire whose length is twice and the radius is half, if it is made of same material is
View Solution
