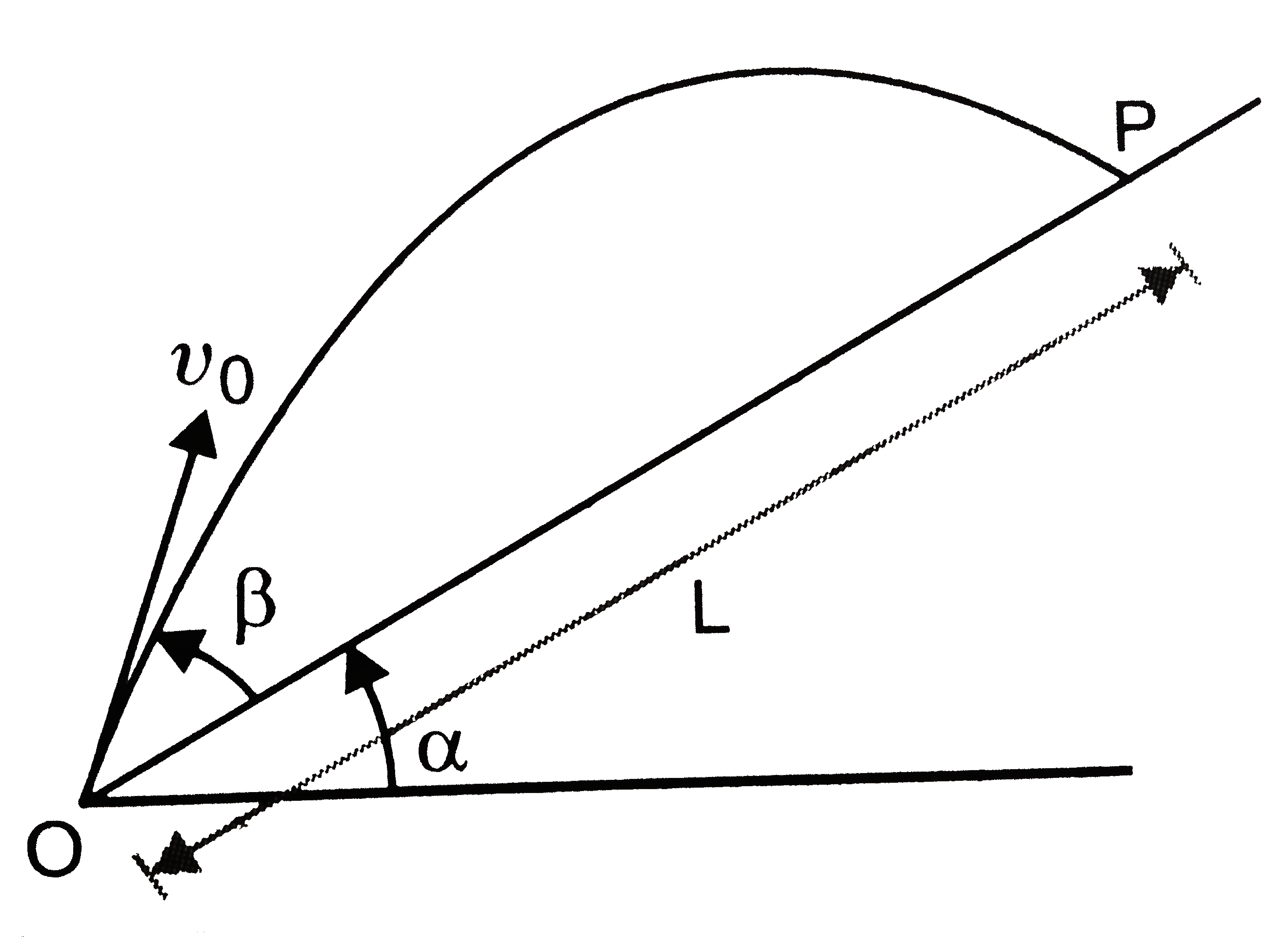
A particle is projected in aIr an angle β to a surface which itself is inclined at an angle α to the horizontal (Fig. 2 (EP). 26)
(a) Find an expression for range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface). (b) Time of flight. 9c ) β at which range will be maximum.
2u2sinαcos(α+β)gcos2α
2u2sinβcos(α+β)gcos2β
2u2sinβcos(α+β)gcos2α
2u2sinαcos(α+β)gcos2β
The correct Answer is:C
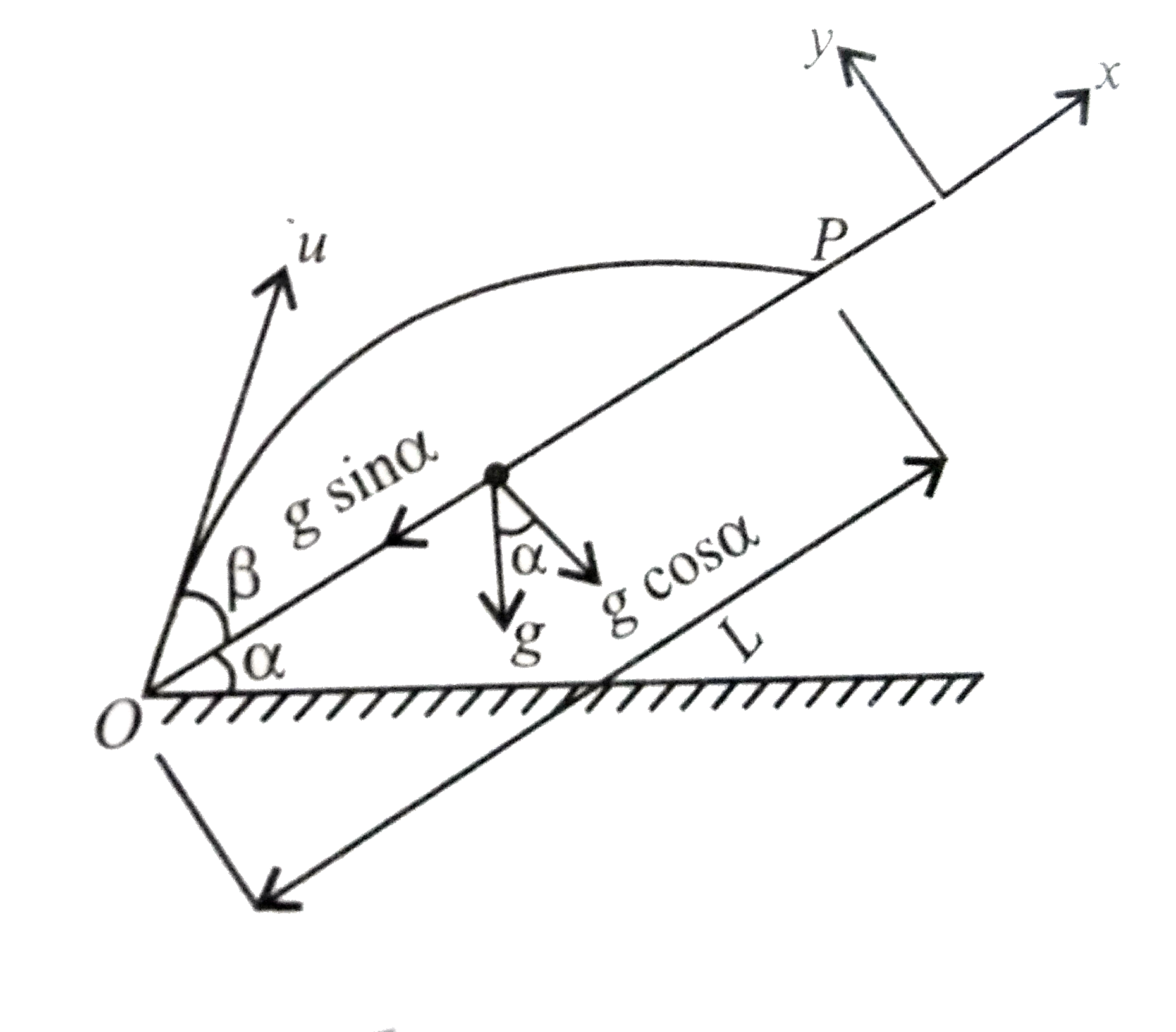
Take the x-axis along the incline and y-axis perpendicular to the plane.
∴uxucosβ
uy=usinβ
ax=−gsinα
ay=−gcosα
When the particle lands at P its y coordinate becomes zero.
∴0=uyt+12ayt2
0=usinβt−12gcosαt2ort=2usinβgcosα ......(i)
For motion along inclined plane, x=uxt+12axt2
∴L=ucosβt−12gsinαt2
Substituting the value of t from eq. (i), we get
L=ucosβ(2usinβgcosα)−12gsinα(2usinβgcosα)2
=2u2sinβcosβgcosα−2u2sinαsin2βgcos2α
=2u2sinβcosβgcosα−2u2sinαsin2βgcos2α
=2u2sinβgcos2α[cosβcosα−sinαsinβ]=2u2sinβcos(α+β)gcos2α
Topper's Solved these Questions
- MOTION IN A PLANE Book:NCERT FINGERTIPSChapter:MOTION IN A PLANE Exercise:Uniform Circular Motion
Explore 14 Videos
- MOTION IN A PLANE Book:NCERT FINGERTIPSChapter:MOTION IN A PLANE Exercise:Miscellaneous Questions
Explore 14 Videos
- MOTION IN A PLANE Book:NCERT FINGERTIPSChapter:MOTION IN A PLANE Exercise:Relative Velocity In Two Dimensions
Explore 4 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTIPSChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assertion And Reason
Explore 15 Videos
- MOTION IN A STRAIGHT LINEBook:NCERT FINGERTIPSChapter:MOTION IN A STRAIGHT LINEExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
A particle is projected in aer an angle β to a surface which itself is inclined at an angle α to the horixonta (Fig. 2 (EP). 26)
(a) Find an ecxpression for range on the plane surface (distanc eon the plance from the point of projection at which particle will hit the surface). (b) Time of flight. 9c ) β at which range will be maximum.

View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View Solution
Knowledge Check
A particle I projected at an angle of elevation α after time t it makes an angle βwith horizontal. The velocity of projection is
A2gtcosβsin(α−β)Bgtcosβsin(α−β)Cgt2sin(α−β)D4gtsin(α−β)A particle is projected at an angle α with the horizontal from the foot of an inclined plane making an angle β with horizontal . Which of the following expressions holds good if the particle strikes the inclined plane normally?
Acotβ=−tan(α−β)Bcotβ=2tan(α−β)Ccotα=tan(α−β)Dcotα=2tan(α−β)A particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)
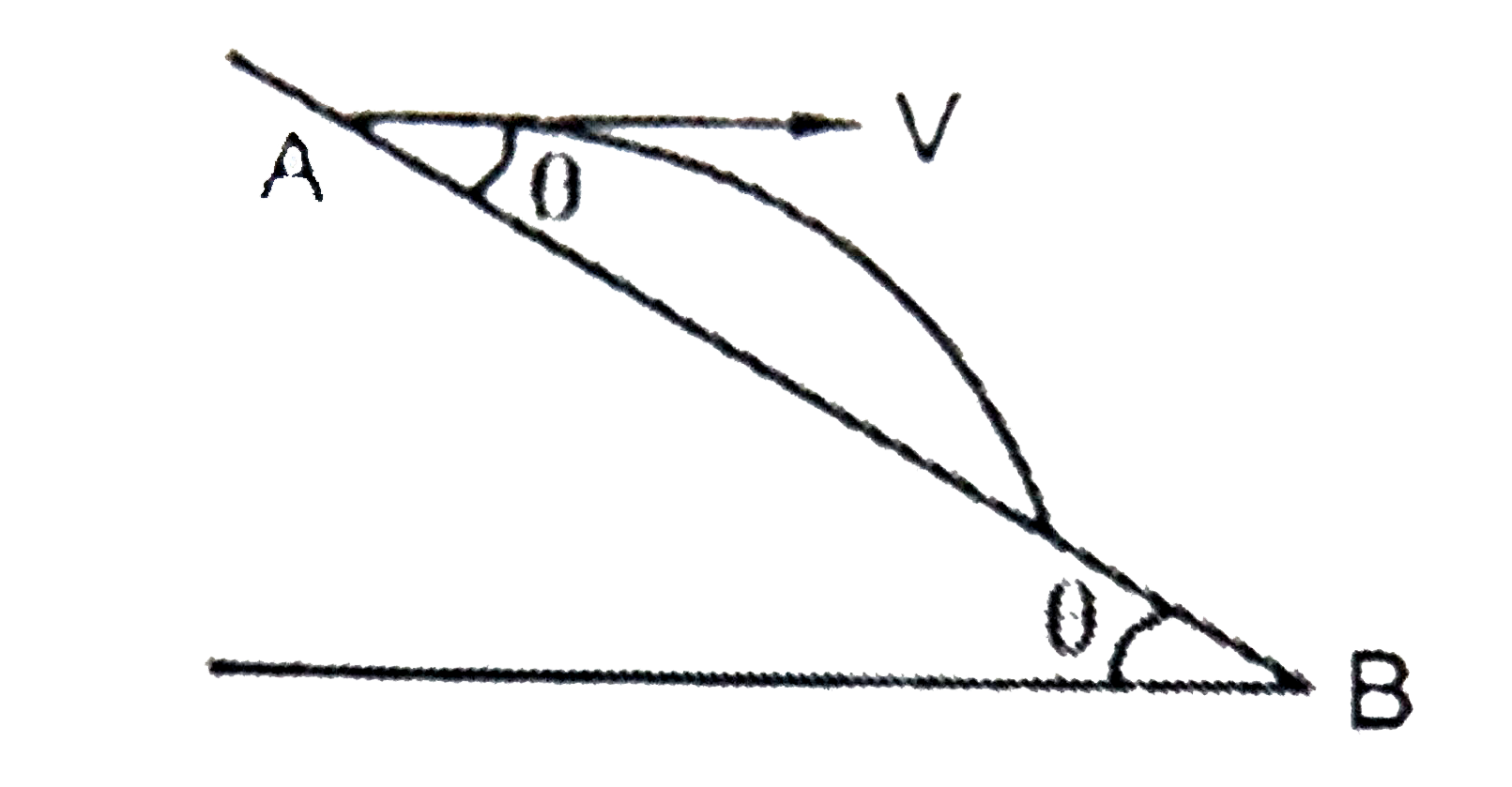
Find the time taken by the particle to hit the plane.A34sB3sC4sD43s
A particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
View SolutionA particle is projected at an angle α with the horizontal.Show that if α is greater than cos−113=70.5∘, the distance of the projectile from the point of projection increases to a maximum above the horizontal plane.
View SolutionThe ratio of the greatest range up an inclined plane through the point of projection and the distance through which a particle falls freely during the corresponding time of flight is
View SolutionA particle is projected at an angle with horizontal. If T is the time of flight and R is a horizontal range, then θ is
View SolutionAn object is projected from A and reaches B on the same horizontal surface. A plane mirror inclined at an angle θ to the horizontal is placed on the ground as shown in the figure. Which of the following best describes the path of the image?

View Solution

