The equation of motion of a projectile is y=ax−bx2, where a and b are constants of motion. Match the quantities in Column I with the relations in Column II.
A
A−p,B−q,C−r,D−s
B
A−s,B−p,C−q,D−r
C
A−s,B−p,C−r,D−q
D
A−p,B−s,C−r,D−q
Video Solution
Text Solution
The correct Answer is:C
Comparing given equation, y=ax−bx2 With the equation of projectile motion y=xtanθ−gx22u2cos2θ
we get, tanθ=a .......(i)
and g2u2cos2θ=b ......(ii)
∴gsec2θ2u2=borg(1+tan2θ)2u2=b
or u2=g(1+tan2θ)2b= (Using(i))
or u=
⎷[g(1+a2)2b],A−s
(B) Horizontal range, R=u2sin2θg=2u2sinθcosθg
R=2u2cos2θg×tanθ=ab (Using (i) and (ii))
B-p
(C) Maximum height, H=u2sin2θ2g
H=u2cos2θ2g×tan2θ=2u2cos2θ4g×tan2thet=a24b
C−r (Using (i) and (ii))
(D) From eqn. (ii),
u2cos2θ=g2borucosθ=√g2b .......(iii)
Time of flight =2usinθg=2ucosθg×tanθ (Using (i) and (iii))
D-q
|
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Uniform Circular Motion
14 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Miscellaneous Questions
14 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Relative Velocity In Two Dimensions
4 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
Match the physical quantity in column I with SI unit in column II.
 A
A B
B C
C D
D
Match the quantities of column I with the corresponding quantities in column II
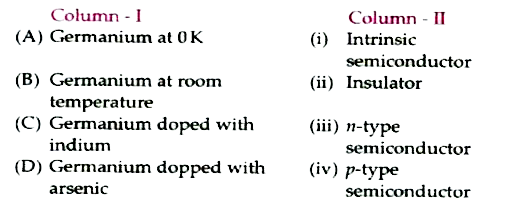 AABCD(i)(ii)(iii)(iv)BABCD(ii)(i)(iv)(iii)CABCD(ii)(i)(iii)(iv)DABCD(i)(ii)(iv)(iii)
AABCD(i)(ii)(iii)(iv)BABCD(ii)(i)(iv)(iii)CABCD(ii)(i)(iii)(iv)DABCD(i)(ii)(iv)(iii)
Match the quantity of Column I with the quantity of Column II

View SolutionMatch the physical quantities in Column I with the units given in Column II.


View SolutionMatch the quantity of column I with the quantity of column II:

View SolutionMatch the quantity of column I with the quantity of column II:

View SolutionMatch the physical quantities in Column -I with their dimensional formula in Column -II

View SolutionMatch each of the equation in Column I with the appropriate entries in Column II.

View Solution


