In an inductor of self-inductance L=2 mH, current changes with time according to relation i=t2e−t. At what time emf is zero ?
4s
3s
2s
1s
The correct Answer is:C
L=2mH=2×10−3H
I=t2e−t
dIdt=t2e−t(−1)+e−t(2t)=te−t(−t+2)
Emf=LdIdt=2×10−3te−1(−t+2)
Now, emf=0, when (−t+2)=0 or t=2s
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:NCERT FINGERTIPSChapter:ELECTROMAGNETIC INDUCTIONExercise:Ac Generator
Explore 4 Videos
- ELECTROMAGNETIC INDUCTIONBook:NCERT FINGERTIPSChapter:ELECTROMAGNETIC INDUCTIONExercise:HIGHER ORDER THINKING SKILLS
Explore 8 Videos
- ELECTROMAGNETIC INDUCTIONBook:NCERT FINGERTIPSChapter:ELECTROMAGNETIC INDUCTIONExercise:Eddy Currents
Explore 4 Videos
- ELECTRIC CHARGES AND FIELDSBook:NCERT FINGERTIPSChapter:ELECTRIC CHARGES AND FIELDSExercise:Assertion And Reason
Explore 15 Videos
- ELECTROMAGNETIC WAVESBook:NCERT FINGERTIPSChapter:ELECTROMAGNETIC WAVESExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
The position vector of a particle changes with time according to the relation →r(t)=15t2ˆi+(4−20t2)ˆj What is the magnitude of the acceleration at t = 1?
View SolutionThe current in a coil of self-inductance 2.0 H is increasing according to I=2sint2 ampere. Find the amount of energy spent during the period when the current charges from zero to 2A.
View Solution
Knowledge Check
In an inductor of inductance L=100mH, a current of I=10A is flowing. The energy stored in the inductor is
A5JB10JC100JD1000JThe inductors of self inductance L1 and L2 are put in series .
AL1+L2onlyBL1−L2onlyCMay be in between L1−L2 and L1+L2DL1+2L2In a certain circuit current changes with time according to i=2√t RMS value of current between t=2s to t=4s will be
A3AB3√3AC2√3AD(2−√2)A
The current in a coil of self inductance 2.0 henry is increasing according to i=2sint2 ampere. Find the amount of energy spent during the period when the current changes from 0 to 2 apere.
View SolutionIn Fig, the mutual inductance of a coil and a very long straight wire is M, coil has resistance R and self-inductance L. The current in the wire varies according to the law I=at, where a is a constant and t is the time, the time dependence of current in the coil is
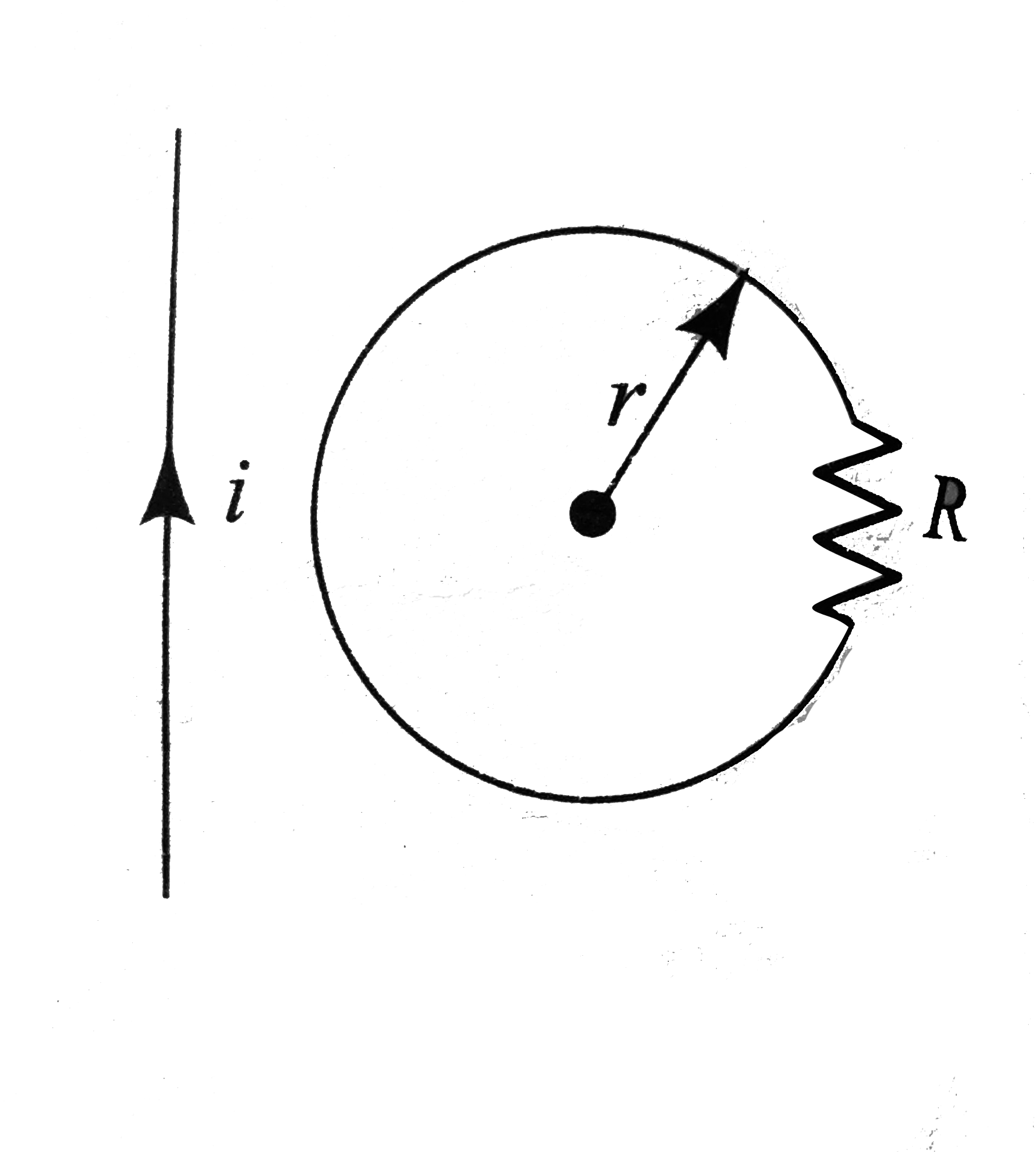
View SolutionFor a coil having L=4 mH , current flow through it is I=t3.e−t then the time at which emf becomes zero
View SolutionTwo identical inductance carry currents that vary with time according to linear laws (as shown in figure). In which of two inductance is the self induction emf greater?

View SolutionWhen a battery is connected across a series combination of self-inductance L and resistance R, the variation in the current I with time t is the best represented by
View Solution

