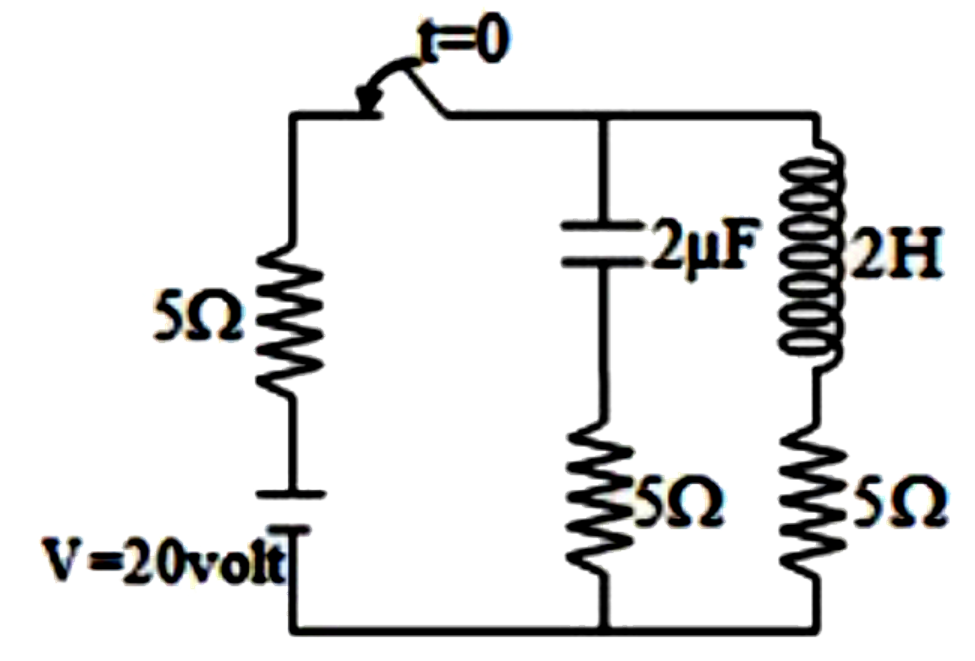
For a coil having L=4 mH , current flow through it is I=t3.e−t then the time at which emf becomes zero
2 sec
1 sec
4 sec
3 sec
The correct Answer is:D
To solve the problem, we need to determine the time at which the induced electromotive force (emf) in a coil becomes zero. The given parameters are:
- Inductance of the coil, L=4mH=4×10−3H
- Current flowing through the coil, I(t)=t3e−t
1. Understand the formula for induced emf:
The induced emf (E) in a coil is given by:
E=−LdIdt
where L is the inductance and dIdt is the rate of change of current with respect to time.
2. Differentiate the current function:
We need to find dIdt for the given current function I(t)=t3e−t. We will use the product rule for differentiation:
dIdt=ddt(t3)⋅e−t+t3⋅ddt(e−t)
Calculating each derivative:
- ddt(t3)=3t2
- ddt(e−t)=−e−t
Therefore,
dIdt=3t2e−t−t3e−t
Simplifying this, we get:
dIdt=e−t(3t2−t3)
3. Substitute dIdt into the emf equation:
Now we substitute dIdt into the emf equation:
E=−L⋅e−t(3t2−t3)
Substituting L=4×10−3:
E=−4×10−3e−t(3t2−t3)
4. Set the emf to zero:
To find the time when the emf becomes zero, we set the equation to zero:
−4×10−3e−t(3t2−t3)=0
Since e−t is never zero for any real t, we can simplify to:
3t2−t3=0
5. Factor the equation:
Factoring out t2:
t2(3−t)=0
This gives us two solutions:
t2=0or3−t=0
Thus,
t=0ort=3
6. Determine the relevant time:
Since we are interested in the time after the current starts flowing, we discard t=0 and take:
t=3seconds
Final Answer:
The time at which the emf becomes zero is t=3seconds.
- Current flowing through the coil, I(t)=t3e−t
The induced emf (E) in a coil is given by:
E=−LdIdt
where L is the inductance and dIdt is the rate of change of current with respect to time.
We need to find dIdt for the given current function I(t)=t3e−t. We will use the product rule for differentiation:
dIdt=ddt(t3)⋅e−t+t3⋅ddt(e−t)
Calculating each derivative:
- ddt(t3)=3t2
- ddt(e−t)=−e−t
dIdt=3t2e−t−t3e−t
Simplifying this, we get:
dIdt=e−t(3t2−t3)
Now we substitute dIdt into the emf equation:
E=−L⋅e−t(3t2−t3)
Substituting L=4×10−3:
E=−4×10−3e−t(3t2−t3)
To find the time when the emf becomes zero, we set the equation to zero:
−4×10−3e−t(3t2−t3)=0
Since e−t is never zero for any real t, we can simplify to:
3t2−t3=0
Factoring out t2:
t2(3−t)=0
This gives us two solutions:
t2=0or3−t=0
Thus,
t=0ort=3
Since we are interested in the time after the current starts flowing, we discard t=0 and take:
t=3seconds
The time at which the emf becomes zero is t=3seconds.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE-2 (C.W)
Explore 22 Videos
- ELECTROMAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE-2 (H.W)
Explore 16 Videos
- ELECTROMAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE-1 (C.W)
Explore 58 Videos
- ELECTRO MAGNETIC WAVESBook:NARAYNAChapter:ELECTRO MAGNETIC WAVESExercise:LEVEL-II(H.W)
Explore 14 Videos
- ELECTROMAGNETIC WAVES Book:NARAYNAChapter:ELECTROMAGNETIC WAVES Exercise:EXERCISE -4
Explore 15 Videos
Similar Questions
Knowledge Check
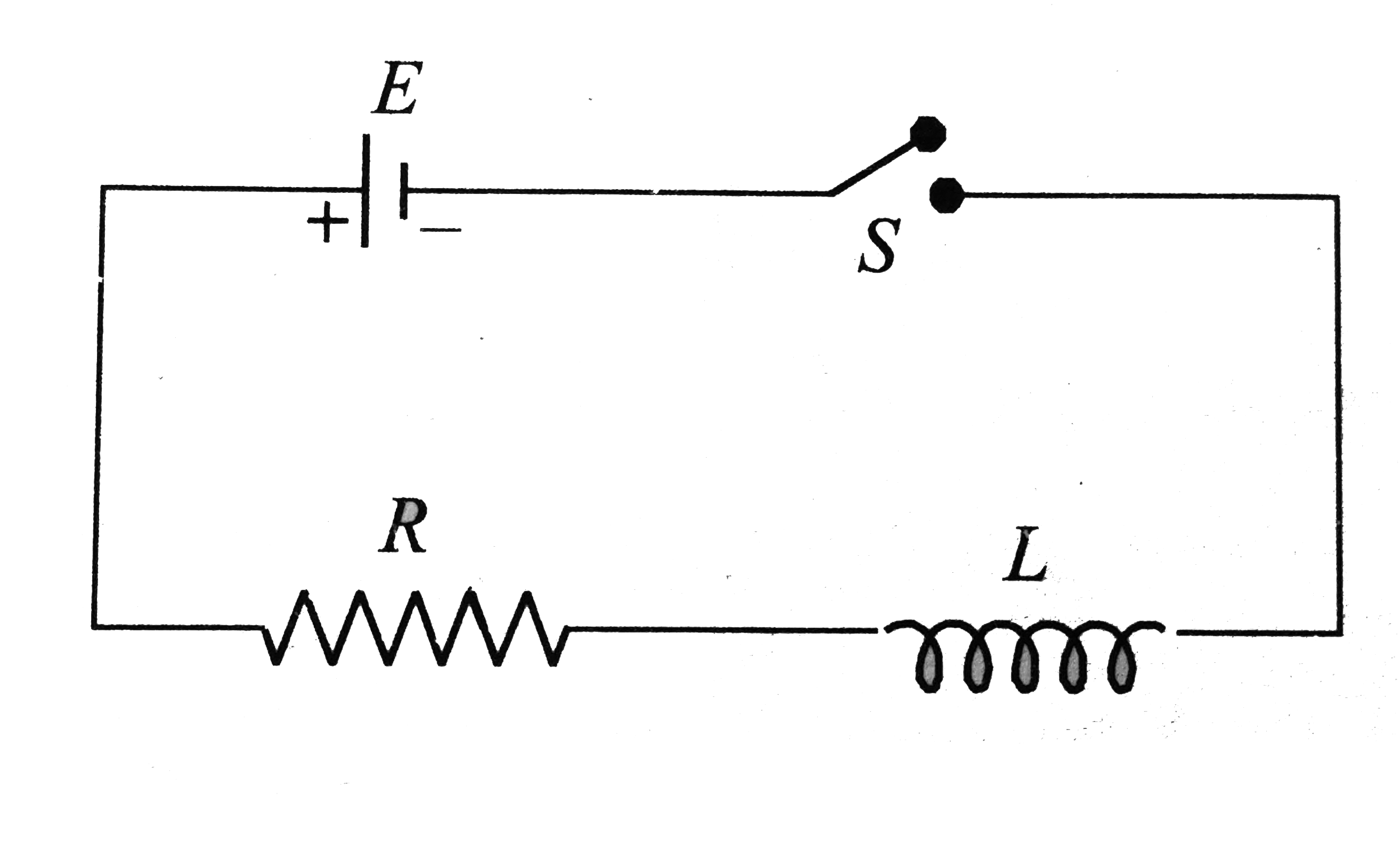
Switch S of the circuit shows in Fig is closed at t=0. If e denotes the induced emf in L and I is the current flowing through the circuit the circuit at time t, which of the following graphs is//are correct?
 A
A B
B C
C D
D
Switch S of the circuit shows in Fig. is closed at t=0. If e denotes the induced emf in L and i the current flowing through the circuit at time t, then which of the following graphs correctly represents the variation of e with i?
 A
A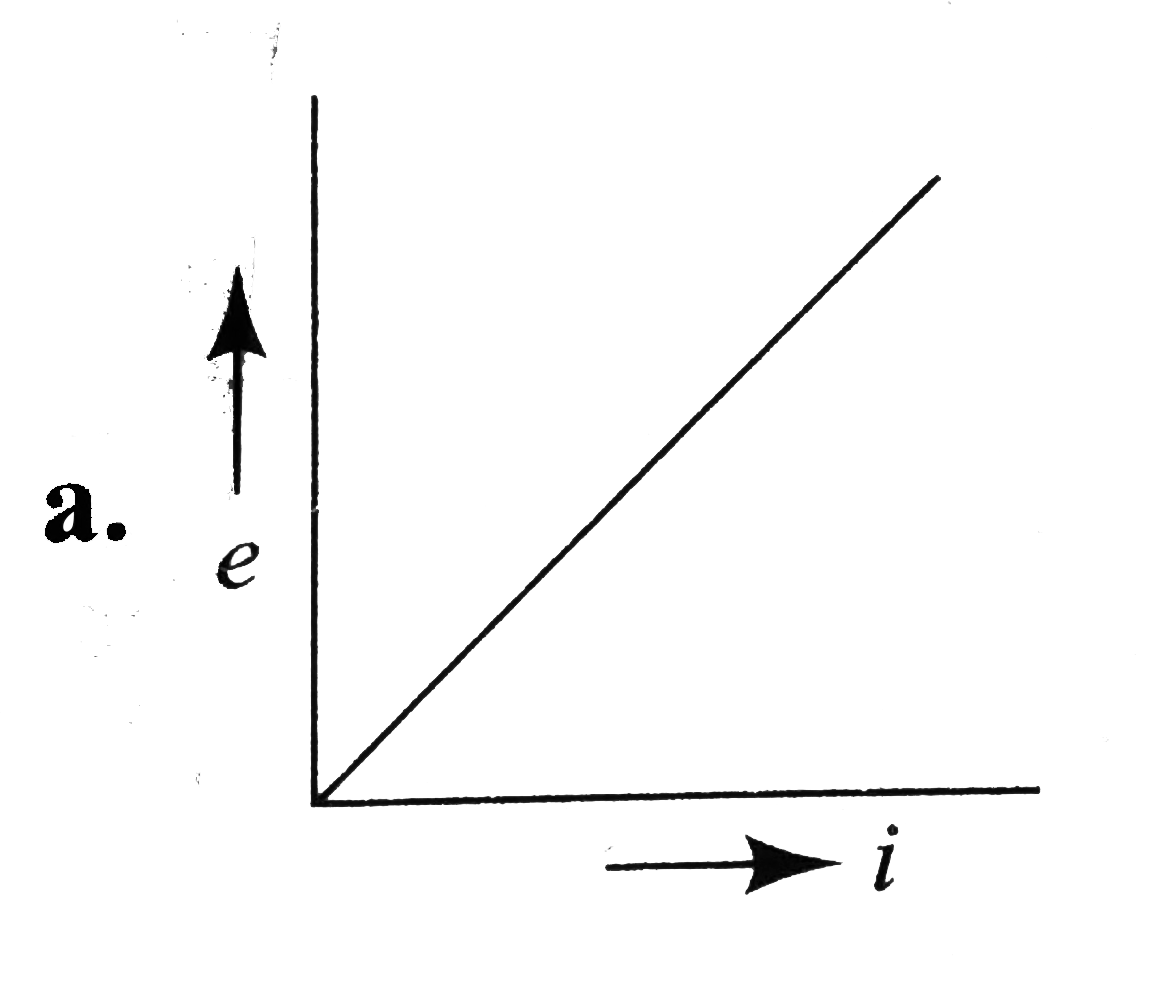 B
B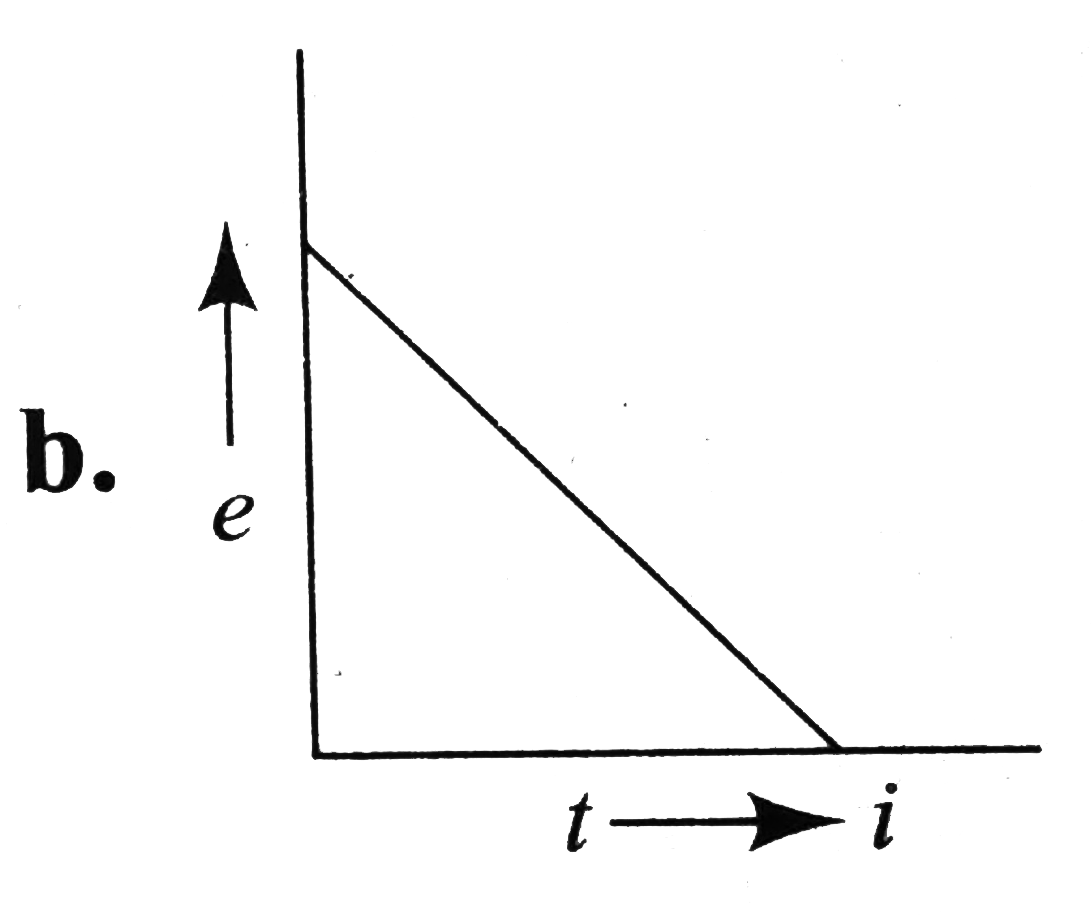 C
C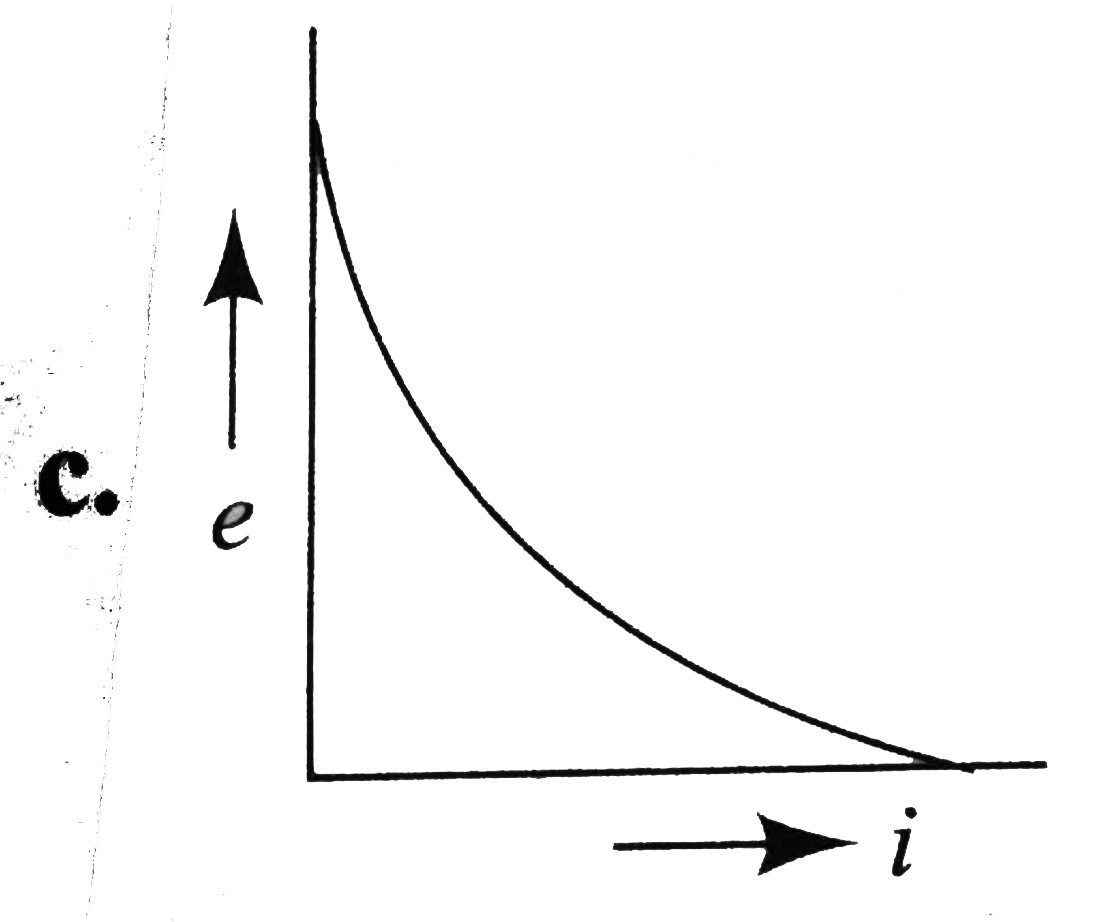 D
D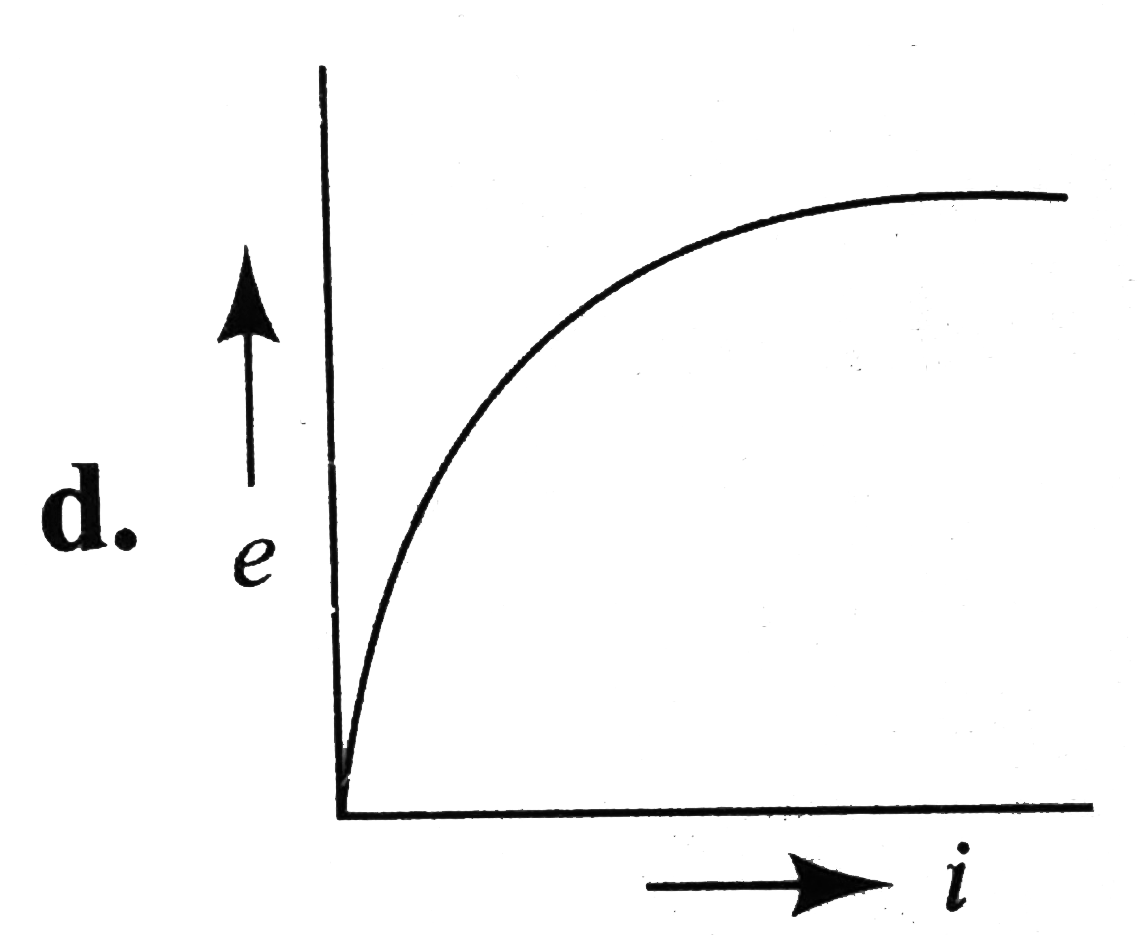
The coefficient of mutual inductance of two coils is 10 mH. IF the current flowing in one coil is 4A then the induced e.m.f in the second coil will be
A40 mVB20 mVCzeroD10 mV
Two neighbouring coils A and B have a mutual inductance of 20 mH. The current flowing through A is given by i=3t2−4t+6. The induced emf at t = 2s is
View SolutionThe coefficient of mutual inductance of two coils is 6mH. If the current flowing in one is 2 ampere, then the induced e.m.f. in the second coil will be
View SolutionSelf-inductance of a coil is 50mH. A current of 1 A passing through the coil reduces to zero at steady rate in 0.1 s, the self-induced emf is
View SolutionTwo neighbouring coils A and B have a mutual inductance of 20 mH. The current flowing through A is given by, i=3t2−4t+6. The induced eml at t=2s is
View SolutionThe current through a coil self inductance L = 2 mH is given by I=t2e−1 at time t. How long it will take to make the e.m.f. zero ?
View Solution