Solve the equation
$2^{| x + 1 |} - 2^{x} = | 2^{x} - 1 | + 1$

Video Solution

Text Solution

Verified by Experts

Find the critical points:brgt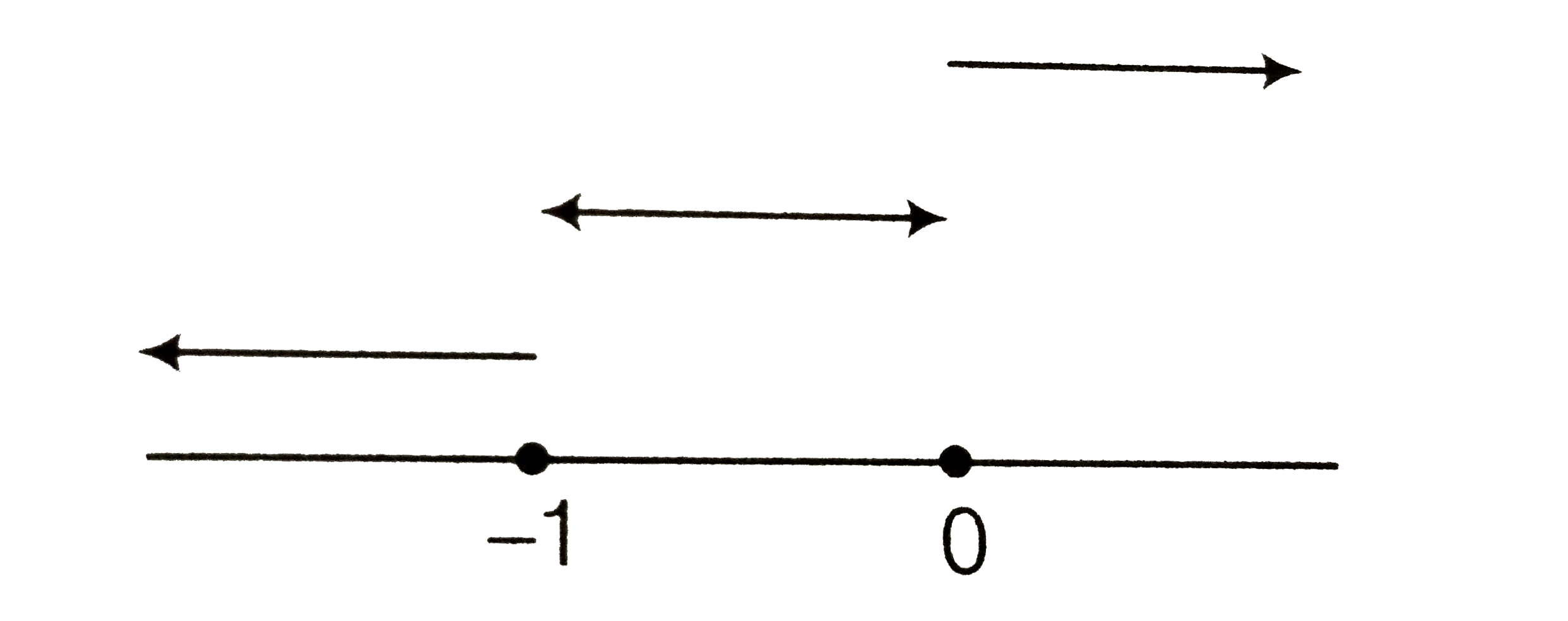
$x + 1 = 0, 2^{x} - 1 = 0$
$∴ x = - 1, x = 0$
Now consider the following cases,
$x < - 1$
$2^{- (x + 1)} - 2^{x} = - (2^{x} - 1) + 1$
$\Rightarrow 2^{- (x + 1)} = 2$
$∴ - (x + 1) = 1$
$∴ x = - 2$ ..i
$- 1 \leq x < 0$ ltbr $2^{x + 1} - 2^{x} = - (2^{x} - 1) + 1$
$\Rightarrow 2^{x + 1} = 2$
$∴ x + 1 = 1$
$∴ x = 0$
$x \neq [∵ - 1 \leq x < 0]$
$x \geq 0$
$2^{x + 1} - 2^{x} = 2^{x} - 1 + 1$
$\Rightarrow 2^{x + 1} = {2.2}^{x}$
$\Rightarrow 2^{x + 1} = 2^{x + 1}$
which is true for $x \geq 0$ ..............ii
Now, combining all cases we have the final solution as
$x ε [0, \infty) \cup {- 2}$

|

Updated on:21/07/2023

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

ARIHANT MATHS-THEORY OF EQUATIONS-Exercise (Questions Asked In Previous 13 Years Exam)

Home
Ask Doubt
Profile