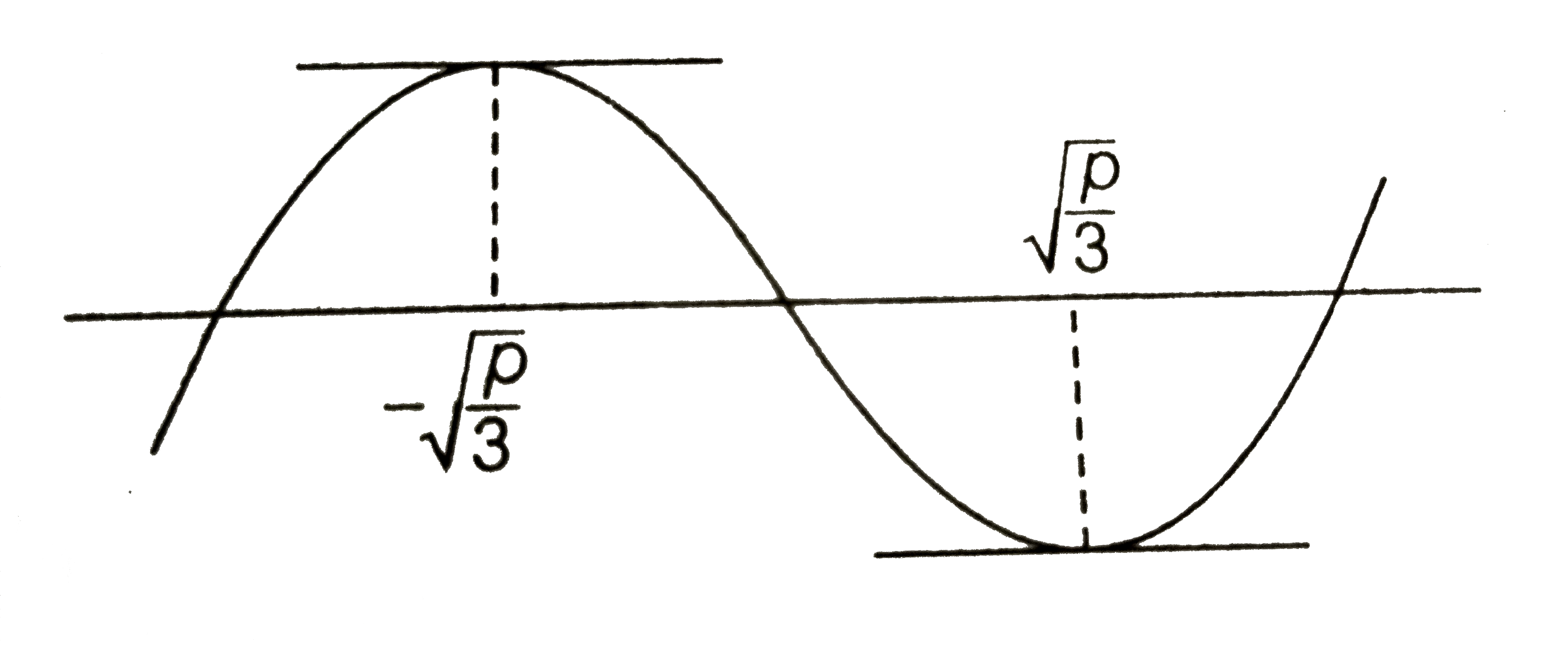
Suppose the cubic $x^{3} - p x + q$ has three distinct real roots, where $p > 0$ and $q > 0$ . Then which one of the following holds?

A

The cubic has minima at $(- \sqrt{\frac{p}{3}})$ and maxima at $\sqrt{\frac{p}{3}}$

B

The cubic has minima at both $\sqrt{\frac{p}{3}}$ and $(- \sqrt{\frac{p}{3}})$

C

The cubic has maxima at both $\sqrt{\frac{p}{3}}$ and $(- \sqrt{\frac{p}{3}})$

D

The cubic has minima at $\sqrt{\frac{p}{3}}$ and maxima at $(- \sqrt{\frac{p}{3}})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Let $f (x) = x^{3} - p x + q$
$∴ f' (x) = 3 x^{2} - p$
$\Rightarrow f'' (x) = 6 x$

For maxima or minima $f' (x) = 0$
$∴ x = \pm \sqrt{\frac{p}{3}}$
$\Rightarrow f'' (\sqrt{\frac{p}{3}}) = 6 \sqrt{(\frac{p}{3})} > 0$
and $f'' (- \sqrt{\frac{p}{3}} = - 6 \sqrt{\frac{p}{3}} < 0$
Hence given cubic minima at $x = \sqrt{\frac{p}{3}}$ and maxima at $x = - \sqrt{\frac{p}{3}}$

|

Updated on:21/07/2023

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Suppose the cubic $x^{3} - p x + q$ has three real roots where $p > 0$ and $q > 0$ . Then which one of the following holds ?
AThe cubic has minimum at both $\sqrt{\frac{p}{3}}$ and - $\sqrt{\frac{p}{3}}$
BThe cubic has maximum at both $\sqrt{\frac{p}{3}}$ and - $\sqrt{\frac{p}{3}}$
CThe cubic has minimum at $\sqrt{\frac{p}{3}}$ and maximum at $- \sqrt{\frac{p}{3}}$
DThe cubic has minimum at $- \sqrt{\frac{p}{3}}$ and maximum at $\sqrt{\frac{p}{3}}$
Question 2 - Select One
If $x^{2} - p x + q = 0$ has equal integral roots, then
Ap and q are even integers
Bp and q are odd integers
Cp an even integer and q is a perfect square of a positive integer
Dnone of these
Question 3 - Select One
The equal $x^{2} - p x + q = 0, p, q, \in R$ has no real roots if :
A $p^{2} > 4 p$
B $p^{2} < 4 q$
C $p^{2} = 4 q$
Dnone of these

ARIHANT MATHS-THEORY OF EQUATIONS-Exercise (Questions Asked In Previous 13 Years Exam)

Home
Ask Doubt
Profile