The smallest value of k, for which both the roots of the equation, $x^{2} - 8 k x + 16 (k^{2} - k + 1) = 0$ are real, distinct and have values at least 4, is

A

6

B

4

C

2

D

0

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Let $f (x) = x^{2} - 8 k x + 16 (k^{2} - k + 1)$ brgt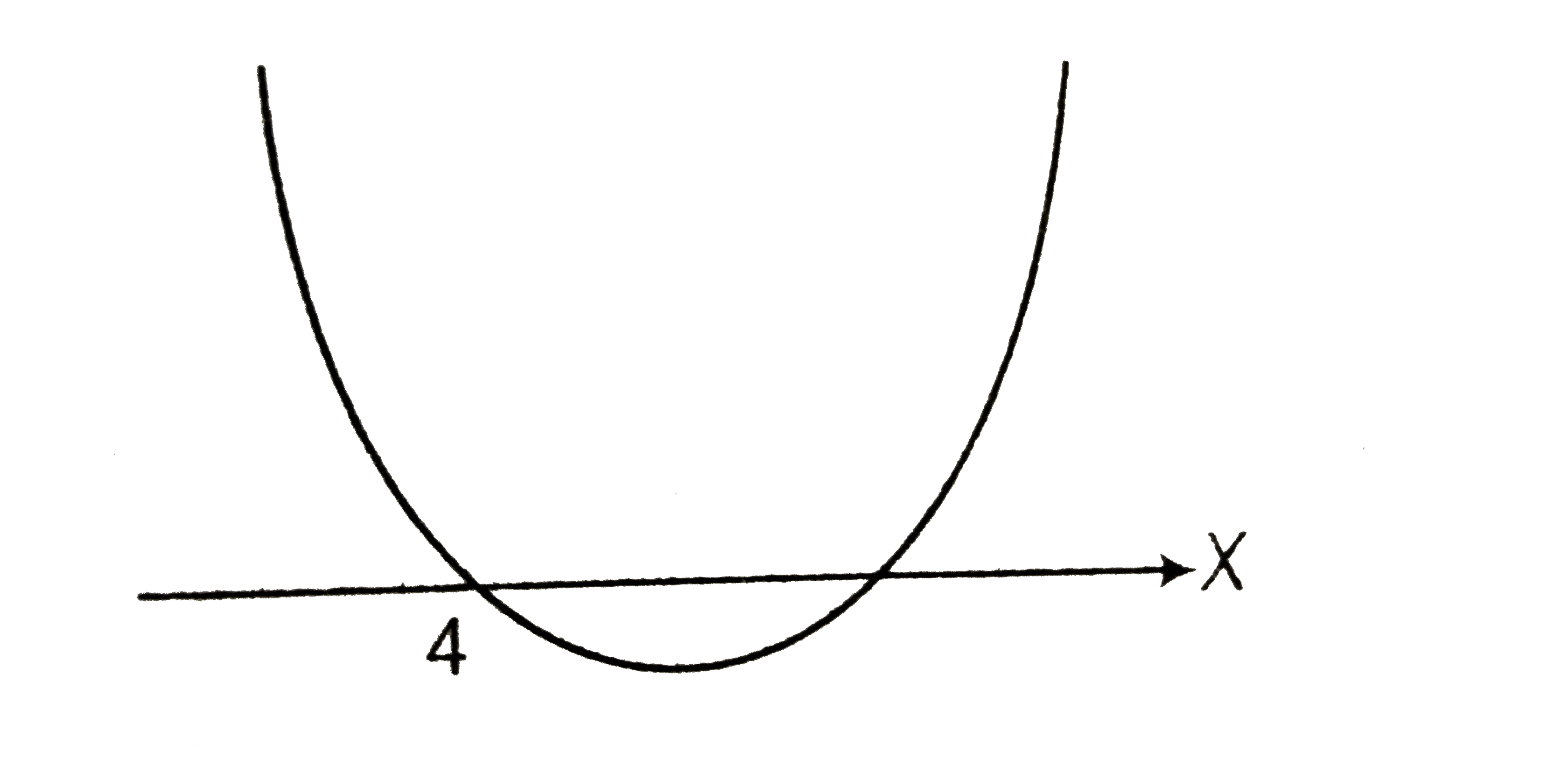
$∴ D > 0$
$\Rightarrow 64 k^{2} - 4.16 (k^{2} - k + 1) > 0$
$\Rightarrow k > 1$ …….i
$\Rightarrow \frac{- b}{2 a} > 4 \Rightarrow \frac{8 k}{2} > 4$
$\Rightarrow k > 1$ ………….ii
and $f (4) \geq 0$
$\Rightarrow 16 - 32 k + 16 (k^{2} - k + 1) \geq 0$
$\Rightarrow k^{2} - 3 k + 2 \geq 0$
$\Rightarrow (k - 1) (k - 2) \geq 0$
$k \leq 1$ or $k \geq 2$ ...........iii
From Eqs i, ii and iii we get
$k \geq 2$
$k_{min} = 2$

Updated on:21/07/2023

|

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The value of k for which both the roots of the equation $4 x^{2} - 20 k x + (25 k^{2} + 15 k - 66) = 0$ are less than 2, lies in
A(4/5,2)
B(2,0)
C(-1,-4/5)
D $(- \infty, - 1)$
The value of k for which the equation $(k - 2) x^{2} + 8 x + k + 4 = 0$ has both roots real, distinct and negative, is
A0
B2
C3
D-4

ARIHANT MATHS-THEORY OF EQUATIONS-Exercise (Questions Asked In Previous 13 Years Exam)

Home
Ask Doubt
Profile