Solve the inequation log(x−3)(2(x2−10x+24)≥lolg(x−3)(x2−9)
Video Solution
Text Solution
This inequation is equivalent to the collection of systems
⎧⎪⎨⎪⎩2(x2−10x+24)≥x2−9x2−9>0x−3>1
⎧⎪
⎪⎨⎪
⎪⎩2(x2−10x+24)≤x2−92(x2−10x+24)>00<x−3<1
On solving the first system, we have
⎧⎪⎨⎪⎩x2−20x+57≥0(x+3)(x−3)>0x>4
⇔⎧⎪
⎪
⎪⎨⎪
⎪
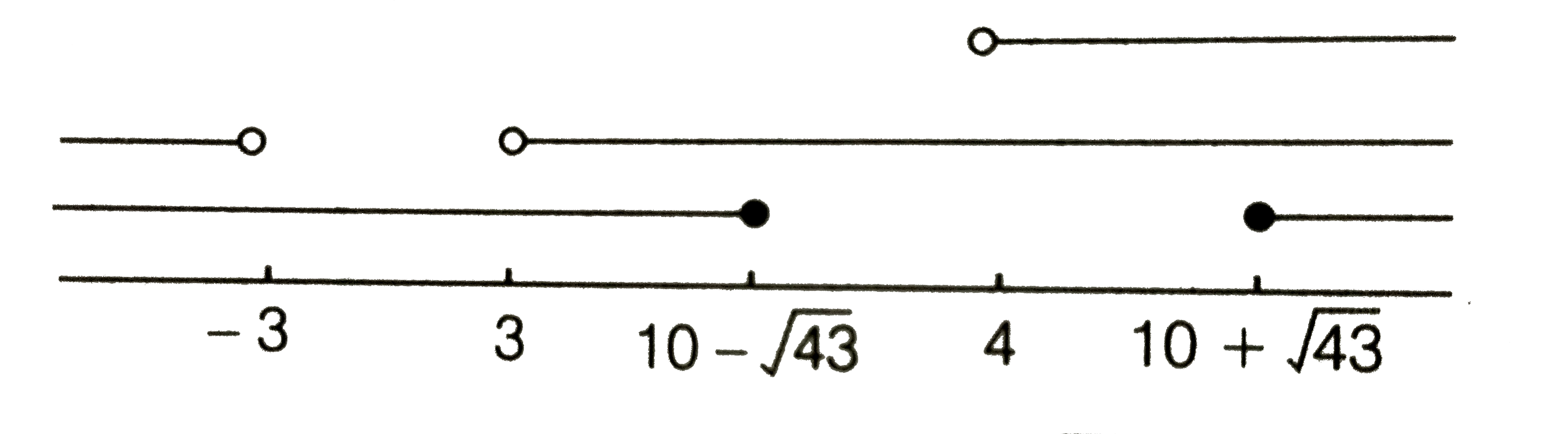
⎪⎩xε(−∞,10−√43]∪[10+√43,∞)xε(−∞,−3)∪(3,∞)xε(4,∞)
Therefore, the system has solution
x≥10+√43
i.e. xε[10+√43,∞)

|
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise For Session 1
11 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise For Session 2
10 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
44 Videos
Similar Questions
Solve the inequation log|x|(√(9−x2)−x−1)≥1
View SolutionSolve the inequation: |x+3|+xx+2>1
View SolutionSolve the inequation log2x+3x2<log2x+3(2x+3)
View SolutionSolve the inequation log(x2−12x+3010)(log2(2x5))>0
View SolutionSolve the inequation logx2+2x−3(|x+4|−|x|x−1∣>0
View SolutionSolve the equation: log2x+3x2<log2x(2x+3)
View SolutionSolve the inequality √(log)2(2x−3x−1)<1
View SolutionSolve the inequality : xlogx>10.
View SolutionSolve the inequality: logx−2(2x−3)>logx−2(24−6x)
View SolutionSolve the inequation 3x+2>(19)1/x.
View Solution
