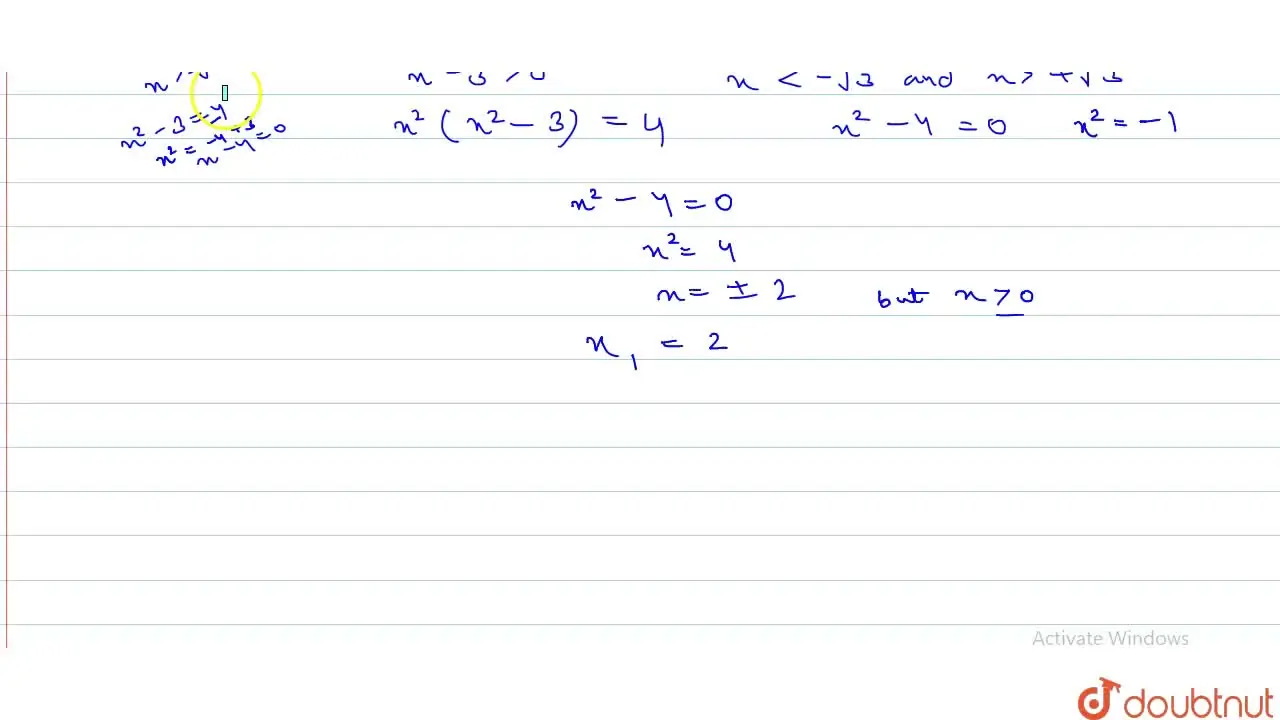Solve the equation 2log3x+log3(x2−3)=log30.5+5log5(log38)
This equation can be written as
log3x2+log3(x2−3)=log30.5+log38
log3x2+log3(x2−3)=log3(4)
This is equivalent to the system
⎧⎪
⎪⎨⎪
⎪⎩x2>0x2−3>0x2(x2−3)=4⇒⎧⎪
⎪⎨⎪
⎪⎩x<0andx>0x<−√3andx>√3(x2−4)(x2=1)=0
⇒x2−4=0∴x=±2, but x>0
Consequently x1=2 is only root of the original equation.
Related Playlists
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise For Session 111videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise For Session 210videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)18videos
THE STRAIGHT LINES
- BOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)44videos
THREE DIMENSIONAL COORDINATE SYSTEM
Similar Questions
Solve the equation log3(5+4log3(x−1))=2
View SolutionSolve the equation: log2x+3x2<log2x(2x+3)
View SolutionFind positive no. x which satisfy the equation log3x⋅log4x(log5x−1)=log5x⋅(log4x+log3x)
View SolutionFind the square of the sum of the roots of the equation log3x⋅log4x⋅log5x=log3x⋅log4x+log5x⋅log3x.
View SolutionThe set of all solutions of the equation log3xlog4xlog3x=log3xlog4x+log4xlog5x+log5xlog3x is
View SolutionThe equation log5x+(log(x2+3)25)−1=log2510 has
View SolutionThe set of all solutions of the equation log3xlog4xlog5x=log3xlog4x+log4xlog5x+log5x+log3x is
View SolutionThe number of solutions of equation log3xlog4xlog5x=log3xlog4x+log5x
View Solutionlog3(5+x)+log88=22
View SolutionFind the square of the sum of the roots of the equation
log3x.log4x.log5x=log3x.log4x+log4x.log5x+log5x.log3xView Solution