Find the values of 'a' for which $- 3 < \frac{x^{2} + a x - 2}{x^{2} + x + 1} < 2$ is valid for all real $x .$

Video Solution

Text Solution

Verified by Experts

The system is equivalent to
$⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ \begin{matrix} \frac{x^{2} - (a + 2) x + 4}{x^{2} - x + 1} > 0 \frac{4 x^{2} + (a - 3) x + 1}{x^{2} - x + 1} > 0 \end{matrix}$
since $x^{2} - x + 1 = {(x - \frac{1}{2})}^{2} + \frac{3}{4} > 0$ , this system is
equivalent to ${\begin{matrix} x^{2} - (a + 2) x + 4 > 0 4 x^{2} + (a - 3) x + 1 > 0 \end{matrix}$
Hence the discriminants of the both equations of this system are negative.
i.e. ${\begin{matrix} {(a + 2)}^{2} - 16 < 0 {(a - 3)}^{2} - 16 < 0 \end{matrix} \Rightarrow (a + 6) (a - 2) < 0$

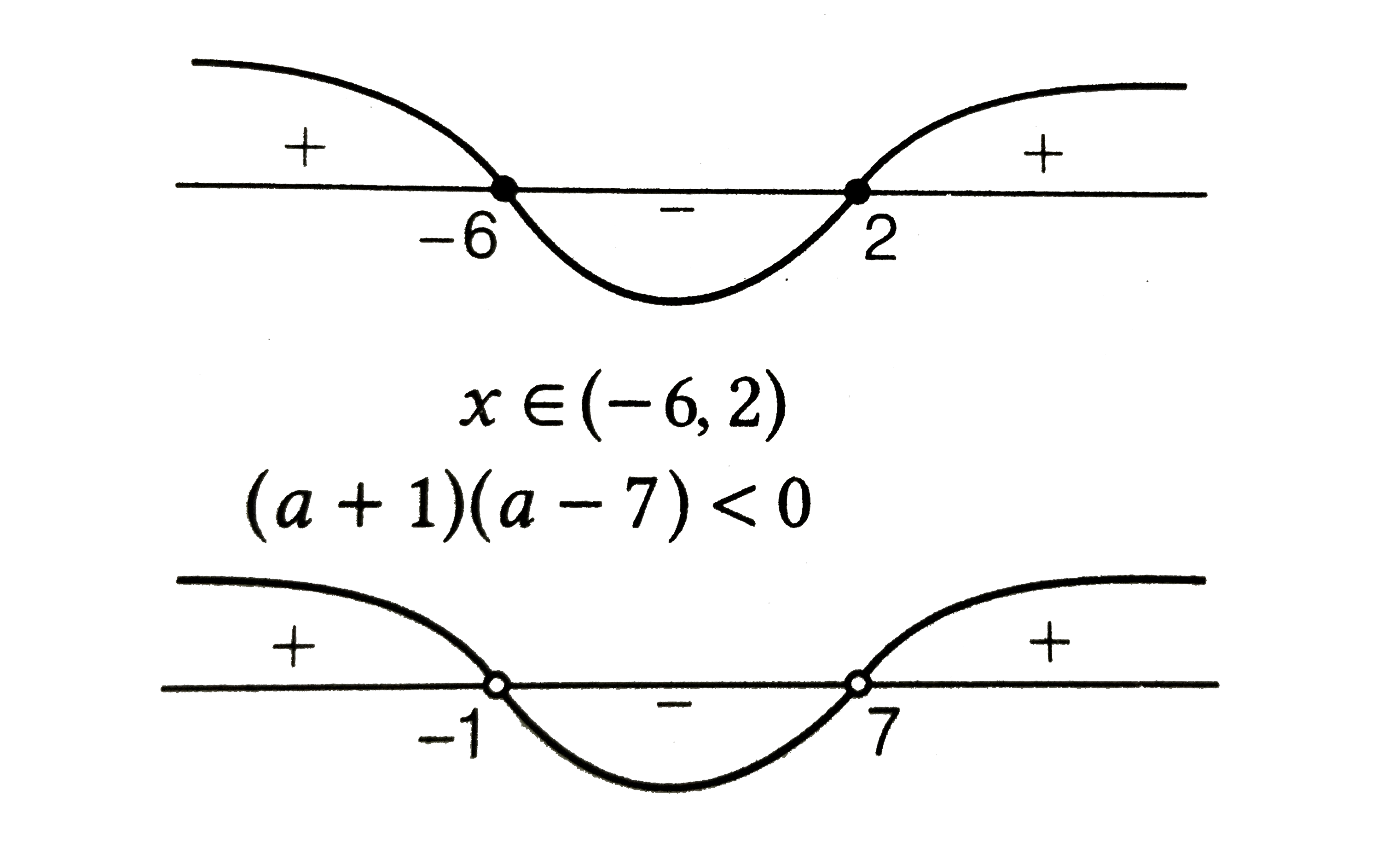
i.e. $x ε (- 1, 7)$
Hence, from Eqs i and ii we get
$x ε (- 1, 2)$

Updated on:21/07/2023

Find the value of 'a' for which $x^{2} + \sqrt{3} x + \frac{a^{2}}{4}$ is a perfect square.
A $\sqrt{3}$
B $2 \sqrt{3}$
C $3 \sqrt{3}$
D $4 \sqrt{3}$
Find the value of $λ$ for which $3 ˆ i + 4 ˆ j - ˆ k and - 2 ˆ i + λ ˆ j + 10 ˆ k$ are perpendicular?
A1
B2
C3
D4
Find the value of $m$ so that ${(- 3)}^{m}^(+ 1) \times {(- 3)}^{5} = {(- 3)}^{7}$
A1
B $- 1$
C0
D4