Let f(x)=(x−3)(x+2)(x+6)(x+1)(x−5) Find intervals where f(x) is positive or negative
Video Solution
Text Solution
We have f(x)=(x−3)(x+2)(x+6)(x+1)(x−5)
The critical points are (−6),(−2),(−1),3,5
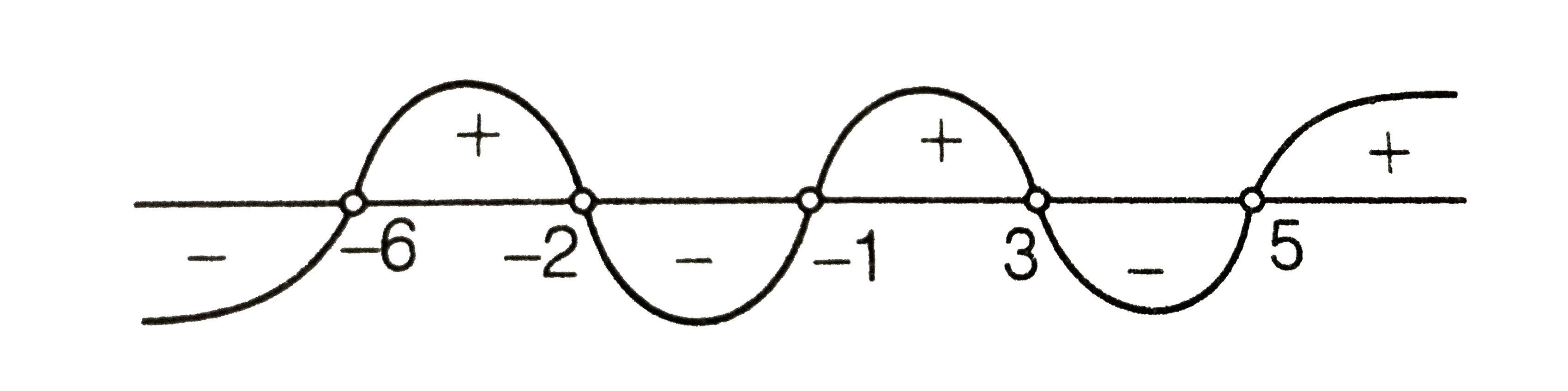
For f(x)>0,Aaxε(−6,−2)∪(−1,3)∪(5,∞)
Fro f(x)<0,∀xε(−∞,−6)∪(−2,−1)∪(3,5)
|
Topper's Solved these Questions
- THEORY OF EQUATIONSBook:ARIHANT MATHSChapter:THEORY OF EQUATIONSExercise:Exercise For Session 1
Explore 11 Videos
- THEORY OF EQUATIONSBook:ARIHANT MATHSChapter:THEORY OF EQUATIONSExercise:Exercise For Session 2
Explore 10 Videos
- THE STRAIGHT LINESBook:ARIHANT MATHSChapter:THE STRAIGHT LINESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 18 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBook:ARIHANT MATHSChapter:THREE DIMENSIONAL COORDINATE SYSTEMExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 44 Videos
Similar Questions
Knowledge Check
Let f(x−1x)=x2+1x2, find the remainder when f(x) is divided by x−3.
A829B83C10D11Let f(x)=∫ex(x−1)(x−2)dx, then f(x) decrease in the interval
A(−∞,−2)B(-2,-1)C(1,2)D(2,∞)Let f(x)=(3x−7)x23. The interval in which f(x) is increasing.
A(0,1415)B(−∞,0)∪(1415,∞)C(−∞,1415)D(0,∞)
Let f(x)=2x+1x , x≠0, where
View SolutionLet f(x)=x2−2xandg(x)=f(f(x)−1)+f(5−f(x)), then
View SolutionLet f(x)=||x|−1|, then points where, f(x) is not differentiable is/are
View SolutionConsider a quadratic expression f(x)=tx2−(2t−1)x+(5x−1)
If f(x) can take both positive and negative values then t must lie in the interval
View SolutionLet f(x)=∫ex(x−1)(x−2)dx. Then f decreases in the interval
View Solution