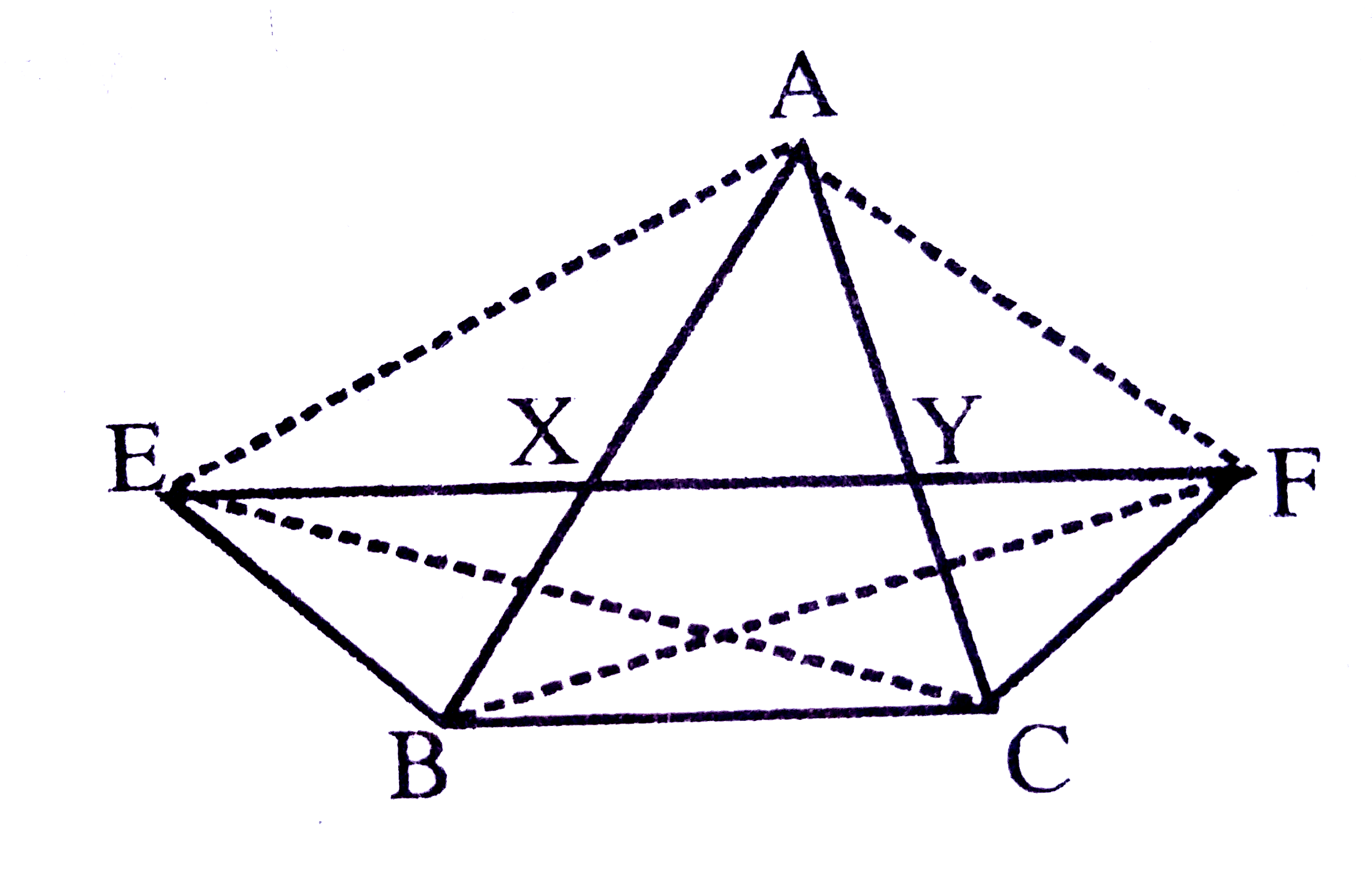
XY त्रिभुज ABC की भुजा BC के समांतर एक रेखा है| यदि BE∣∣AC और CF∣∣AB रेखा XY ar(ABE)=ar(ACF)
BF और CF को मिलाया
प्रमाण : ΔABE और ΔEBC एक ही आधार EB तथा दो समांतर रेखाओ EB और AC के बीच स्थित है|
∴ ar(ΔABE)=ar(ΔEBC) ...(i)
पुनः ΔACF और ΔFBC एक ही आधार CF पर स्थित है तथा दो समांतर रेखाओं AB और CF के बीच स्थित है ltbr gt ∴ ar(ΔACF)=ar(ΔFBC) ....(ii)
हम जानते है की किसी समांतर चतुर्भुज कर्ण उसे दो सर्वांगसम त्रिभुजों में बांटता है
∴समांतर चतुर्भुज EBCY में ar(ΔEBC)=12ar(EBCY) ...(iii)
तथा समांतर चतुर्भुज XBCF में, ar(ΔFBC)=12ar(XBCF) ...(iv)
लेकिन समांतर चतुर्भुज EBCY तथा XBCF एक ही आधार BC पर स्थित है तथा एक ही समांतर रेखाओं BC और XY के बीच स्थित है|
∴ ar(EBCY)=ar(XBCF)
∴ समीकरण (iii ) और (iv ) से, ar(ΔEBC)=ar(ΔFBC)
अतः समीकरण (i ) और (ii ) से ar(ΔABE)=ar(ΔACF)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 11.1
24 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - वस्तुनिष्ट प्रश्न
7 Videos
- समांतर चतुर्भुजBOOK - KC SINHACHAPTER - समांतर चतुर्भुजEXERCISE - वस्तुनिष्ठ प्रश्न
9 Videos
- हीरोन का सूत्र BOOK - KC SINHACHAPTER - हीरोन का सूत्र EXERCISE - वस्तुनिष्ठ प्रश्न
13 Videos
Similar Questions
रिक्त स्थान को भरें :
(i) सर्वांगसम आयतों के क्षेत्रफल ...........होते है|
(ii) किसी समचतुर्भुज का क्षेत्रफल उसके विकर्णों की लम्बाइयों के गुणनफल का .....होता है
(iii) समलम्ब का क्षेत्रफल उसके समांतर भुजाओं के बीच की दुरी तथा समांतर भुजाओं के योग के गुणनफल का ......होता है|
(iv) सर्वांगसम त्रिभुजों के क्षेत्रफल ........होते है|
(v) एक ही आधार तथा एक ही समांतर रेखाओं के मध्य बने त्रिभुज क्षेत्रफल में ...........होते है|
View Solutionसमचतुर्भुज के विकर्णों का गुणनफल समचतुर्भुज के क्षेत्रफल का कितना गुना होता है ?
View Solutionचतुर्भुज के चारों कोणों का योग कितना समकोण होता है?
View Solutionयदि किसी ΔABC में BC=a,CA=b AB=c हो तो ΔABC की अर्धपरिमिति है
View Solutionत्रिभुज ABC की भुजा BC के समांतर एक रेखा XY है। यदि BE ।। AC तथा CF ।। AB रेखा XY को क्रमशः E तथा F पर मिलते है तो सिद्ध कीजिए कि ar(ΔABE)=ar(ΔACF).
View SolutionXY त्रिभुज ABC की भुजा BC के समान्तर एक रेखा है। यदि BE || AC और CF || AB रेखा XY से क्रमशः E और F पर मिलती है, तो दर्शाइए कि :
ar(ABE) = ar(ACF)
View SolutionΔABC कि भुजा BC के समांतर XY रेखा है, BE∣∣AC और CF∣∣AB खींचे जो XY को क्रमश : E और F पर काटती है । सिद्ध करे कि ar(ΔABE)=ar(ΔACF).
View Solutionएक रेखा AB के कार्तीय समीकरण 2x−1√3=y+22=z−33 है। AB के समांतर रेखा की दिक् कोज्याएं ज्ञात कीजिए।
View Solutionएक रेखा AB के समीकरण 3−x1=y+2−2=z−54 है। AB के समांतर रेखा दिक्-अनुपात लिखिए।
View SolutionXY is a line parallel to side BC of a triangle ABC. If BF ||AC and CF || AB meet XY at E and F respectively, show that ar (ABE) = ar (ACF)
View SolutionXY is a line parallel to side BC of a triangle ABC. If BE||AC and CF ||AB meet XY at E and F respectively , show that ar(ABE)=ar(ACF)

View SolutionXY is a line parallel to side BC of triangle ABC. If BEIIAC and CFIIAB meet XY at E and F respectively,show that ar (ABE) = ar (ACF).
View SolutionXY ਤ੍ਰਿਭੁਜ ABC ਦੀ ਭੁਜਾ BC ਦੇ ਸਮਾਂਤਰ ਇੱਕ ਰੇਖਾ ਹੈ। ਜੇਕਰ BE || AC ਅਤੇ CF || AB ਰੇਖਾ XY ਨੂੰ ਕ੍ਰਮਵਾਰ E ਅਤੇ F 'ਤੇ ਮਿਲਦੀ ਹੈ, ਤਾਂ ਦਰਸਾਓ ਕਿ:-ar (ABE) = ar (ACF)
View Solutionरेखाएँ एवं कोण|समांतर रेखा और तिर्यक रेखा#!#समांतर रेखा और तिर्यक रेखा पर आधारित प्रश्न
View SolutionIn triangle ABC a straight line parallel to BC intersects AB and AC at D and E respectively. If AB = 2AD, then DE : BC is - त्रिभुज ABC में BC के समांतर एक सरल रेखा AB और AC को क्रमशः D और E पर काटती है । यदि AB= 2AD, तो DE : BC कितना होगा ।
View SolutionA circle is inscribed in triangle ABC , touching AB at P, BC at Q and AC at R. If AR=5 cm, RC= 6 cm and AB=12 cm, then perimeter of triangle ABC is: एक वृत्त किसी त्रिभुज ABC में समाहित है जो AB को P पर, BC को Q पर तथा AC को R पर स्पर्श करता है | यदि AR =5 सेमी और AB = 12 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
View Solution
