त्रिभुज ABC की भुजा BC के समांतर एक रेखा XY है। यदि BE ।। AC तथा CF ।। AB रेखा XY को क्रमशः E तथा F पर मिलते है तो सिद्ध कीजिए कि ar(ΔABE)=ar(ΔACF).
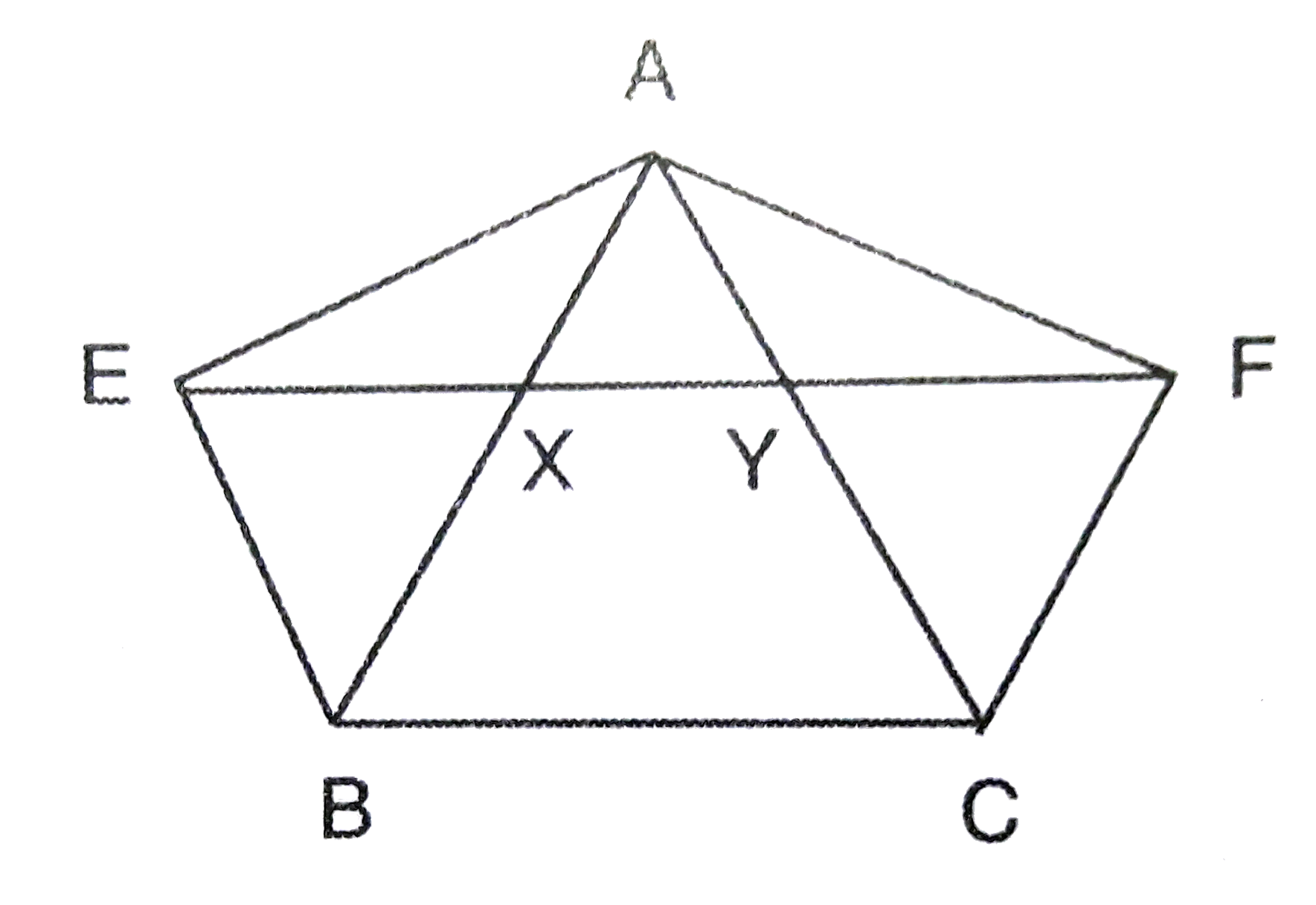
चूँकि XY ।। BC तथा BE ।। CY अतः, BCYE एक समांतर है।
क्योंकि ΔABE तथा ।।gmBCYE एक ही आधार BE तथा समान समांतर रेखाओं BE तथा AC के बीच स्थित है।
∴ar(ΔABE)=12ar (समांतर चतुर्भुज BCYE ) ... (i )
अब CF ।। AB तथा XY ।। BC
⇒ CF ।। AB तथा XF ।। BC
⇒ BCFX एक समांतर चतुर्भुज है।
चूँकि ΔACF तथा ।।gmBCFX एक आधार CF तथा समान समांतर रेखाओं AB तथा FC के बीच स्थित हैं।
∴ar(ΔACF)=12ar(।।gmBCFX) ... (ii)
परन्तु ।।gmBCFX एक ही आधार BC तथा समान समांतर रेखाओं BC तथा EF के बीच स्थित हैं।
∴ar(।।gmBCFX)=ar(।।gmBCYE) ...(iii)
(i), (ii) तथा (iii ) से,
ar(ΔABE)=ar(ΔACF)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - व्याख्यात्मक उदाहरण
1 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 15.1
6 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण BOOK - RD SHARMACHAPTER - संख्यिकीय आंकड़ों का आलेखीय निरूपण EXERCISE - बहु विकल्पीय प्रश्न
8 Videos
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - बहु विकल्पीय प्रश्न
17 Videos
Similar Questions
चित्र में , P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिंदु है दर्शाइए कि
(i) ar(ΔAPB)+ar(ΔPCD)=12ar(।।gmABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)

View Solutionआकृति में आकृति एक ही आधार तथा समान समांतर रेखाओं के बीच स्थित है :

View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View SolutionΔABC कि भुजा BC के समांतर XY रेखा है, BE∣∣AC और CF∣∣AB खींचे जो XY को क्रमश : E और F पर काटती है । सिद्ध करे कि ar(ΔABE)=ar(ΔACF).
View Solutionदी गई आकृति AT वृत्त की स्पर्श रेखा है। यदि m∠ABC=50∘ तथा AC=BC तो ∠BAT है -

View Solutionमाना बिंदु (h,k), (1,2) तथा (−3,4) एक रेखा L1 पर स्थित है। यदि बिन्दुओ (h,k) तथा (4,3) से होकर जाने वाली रेखा L2 रेखा L1 के लंबवत है, तो kh बराबर है
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View SolutionIn the figure, XY is a line parallel to BC is drawn through A. If BE || CA and CF || BA are drawn to meet XY at E and F respectively. Show that ar(ΔABE)=ar(ΔACF).
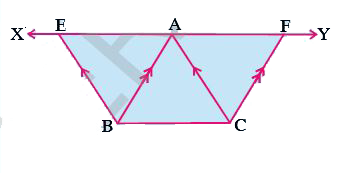
View SolutionIn the figure, XY is a line parallel to BC is drawn through A. If BE || CA and CF || BA are drawn to meet XY at E and F respectively. Show that ar(ΔABE)=ar(ΔACF).
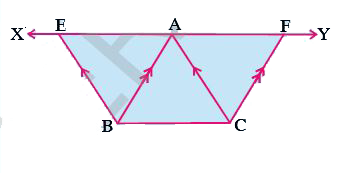
View SolutionIn the figure, XY is a line parallel to BC is drawn through A. If BE || CA and CF || BA are drawn to meet XY at E and F respectively. Show that ar(ΔABE)=ar(ΔACF).
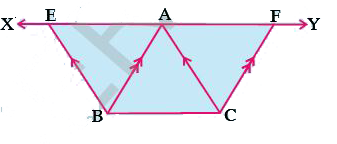
View SolutionXY is a line parallel to side BC of a triangle ABC. If BE||AC and CF ||AB meet XY at E and F respectively , show that ar(ABE)=ar(ACF)

View SolutionIn a triangle ABC, AB = 12, BC =18 and AC = 15. The medians AX and BY intersect sides BC and AC at X and Y respectively. If AX and BX intersect each other at O, then what is the value of OX? एक त्रिभुज ABC में, AB = 12, BC =18 तथा AC = 15 है। मध्य रेखा AX तथा BY, भुजा BC तथा AC को क्रमशः X तथा Y पर प्रतिच्छेद करती है। यदि AX तथा BY, O पर प्रतिच्छेदन करते हैं, तो OX का मान क्या है?
View Solution
